[Topological Data Analysis의 기초]

본 포스팅 시리즈는 위상수학적 데이터 분석(Topological Data Analysis; TDA)의 기초 토대를 다지고자 만들어졌습니다.

TDA는 그 매력과 성과에 비해 비교적 덜 알려졌다고 생각합니다.
그래서 여러 학회에 TDA를 응용한 연구결과들을 발표할 때마다, 제한된 시간 내에 TDA의 매우 기초적인 개념부터 설명해야 한다는 점은 굉장히 저를 비롯한 TDA를 연구하는 동료들에게 고역인 일이라고 생각합니다.
본 포스팅 시리즈가 마무리되면, TDA를 짧은 시간 내에 핵심적인 아이디어만 소개할 수 있는 노하우가 생기길 기대합니다.

한편, 어쩌다 TDA를 알게되신 분들이 흥미를 가지고 TDA를 입문하고자 할 때에 입문용 자료가 많이 없어 어려움을 겪곤 하는 것을 보았습니다.
TDA에 사용되는 수학적 개념들은 평범한 수학과 학부생들도 다 익히기 어려운 개념들이 등장하곤 합니다.
특히 TDA에서 주로 사용하는 도구는 지속성 호몰로지(Persistent homology)인데, 호몰로지라는 이름부터 벌써 두려운데 거기에 지속성이라는 말까지 붙었으니, 얼마나 두려운 개념이겠습니까?
이 포스팅 시리즈를 통해 복합체(Complex), 호몰로지(Homology), 지속성 호몰로지(Persistent homology) 등의 개념을 최대한 쉽게 설명해보려 노력할 것입니다.

그러나 필자가 수학 비전공자에 대한 '공감능력' 부족으로 여전히 이해하기 어려운 설명이 있을 수 있습니다.
그런 부분에 대해 코맨트를 남겨주신다면, 정말 감사드리겠습니다.

📄 참고문헌
1. Carlsson, Gunnar. "Topology and data." Bulletin of the American Mathematical Society 46.2 (2009)
2. Zomorodian, Afra, and Gunnar Carlsson. "Computing persistent homology." Discrete & Computational Geometry 33.2 (2005)
3. Otter, Nina, et al. "A roadmap for the computation of persistent homology." EPJ Data Science 6 (2017)
4. Edelsbrunner, Herbert, and John L. Harer. "Computational topology: an introduction." American Mathematical Society, 2022

---

§. 3.2.) Category Theory

🚧 주의!!

이번 섹션의 내용은 어렵습니다.
이번 섹션은 사실 범주론 (Category Theory) 내용을 다루고 있습니다.
읽다가 현기증이 난다면, 요약만 읽고 다음 섹션으로 넘어가시길 추천드립니다.

📌 핵심 Keyword

• 범주 (Category) : 어떤 대상들과 그 대상들 사이의 화살표들의 모임.
• 자연스러운 변환(Natural transform) : 두 카테고리를 서로 호환이 되게 연결시켜주는 변환
• 심플리셜 컴플렉스의 카테고리와 이들로부터 유도된 호몰로지의 카테고리는 자연스럽게 연결된다.

지금까지의 과정을 통해 우리가 얻을 수 있는 정보를 요약해봅시다.

1. 필트레이션 $\empty = K_0 \subseteq K_1 \subseteq K_2 \subseteq \cdots \subseteq K_n$
2. 각 서브컴플렉스 $K_i$에 대한 체인 컴플렉스 $\cdots \rightarrow C_{k+1}(K_i) \rightarrow C_k(K_i) \rightarrow\cdots$
3. 각 $C_{k+1}(K_i) \rightarrow C_k(K_i) \rightarrow C_{k-1}(K_i)$에서 얻은 호몰로지 $H_k(K_i)$

정보가 무척이나 많습니다.
이를 그림으로 요약해보겠습니다.

공간 상에 네 개의 데이터 포인트가 있다고 합시다.
이 네 개의 포인트를 점차 연결해나가며 이 데이터의 기하학적 정보를 알아내고자 합니다.

각 서브컴플렉스 $K_i$에 대해 세로로 나열된 정보는 우리가 획득할 수 있습니다.
그러나 우리가 필요한 정보는 $K_i$에서 $K_{i+1}$로 어떻게 기하학적 특성이 변해가는지 입니다.
즉, $H_k(K_i)$에서 $H_k(K_{i+1})$로 정보가 어떻게 변하는지를 알고 싶습니다 (그림에서 파란색 화살표).

여기서 필트레이션 $K_0 \subseteq K_1 \subseteq \cdots \subseteq K_n$에 여러 '심플리셜 컴플렉스'들이 '$\subseteq$'라는 일종의 화살표로 연결되어 있다는 점에 주목합시다.
이처럼 '대상들'과 그 대상들 사이의 관계를 나타내는 '화살표'를 통틀어 범주(Category)라고 합니다.

범주론(Category Theory)에 따르면 어떤 대상들의 모임과 그 대상들의 관계를 나타내는 화살표들의 모임이 주어지면, 그것을 또 다른 대상들의 모임과 그 대상들의 화살표들의 모임으로 '자연스럽게'(naturally) 옮겨주는 변환이 존재합니다.

(예전에 카테고리 이론에 대해 정리한 내용을 업로드했었는데 아직 내용이 미흡하다 생각하여 비공개하였습니다. 추후에 내용을 보완하여 공개하도록 하겠습니다.)

이 변환에 따라 서브컴플렉스들의 모임과 포함관계 $(\left\{K_i\right\}_{i=0}^n, \subseteq)$는 $k$차 호몰로지들의 모임과 포함관계로부터 유도되는 선형변환 $f_{a,b} : H_k(K_a) \rightarrow H_k(K_b)\;\; (a\leq b)$들의 모임 $(\left\{H_k(K_i)\right\}_{i=1}^n, \left\{f_{a,b}\right\}_{a\leq b})$이 자연스럽게 유도됩니다.
이를 심플리셜컴플렉스의 카테고리에서 호몰로지의 카테고리로의 자연스러운 변환(natural transform)이 존재한다고 합니다.

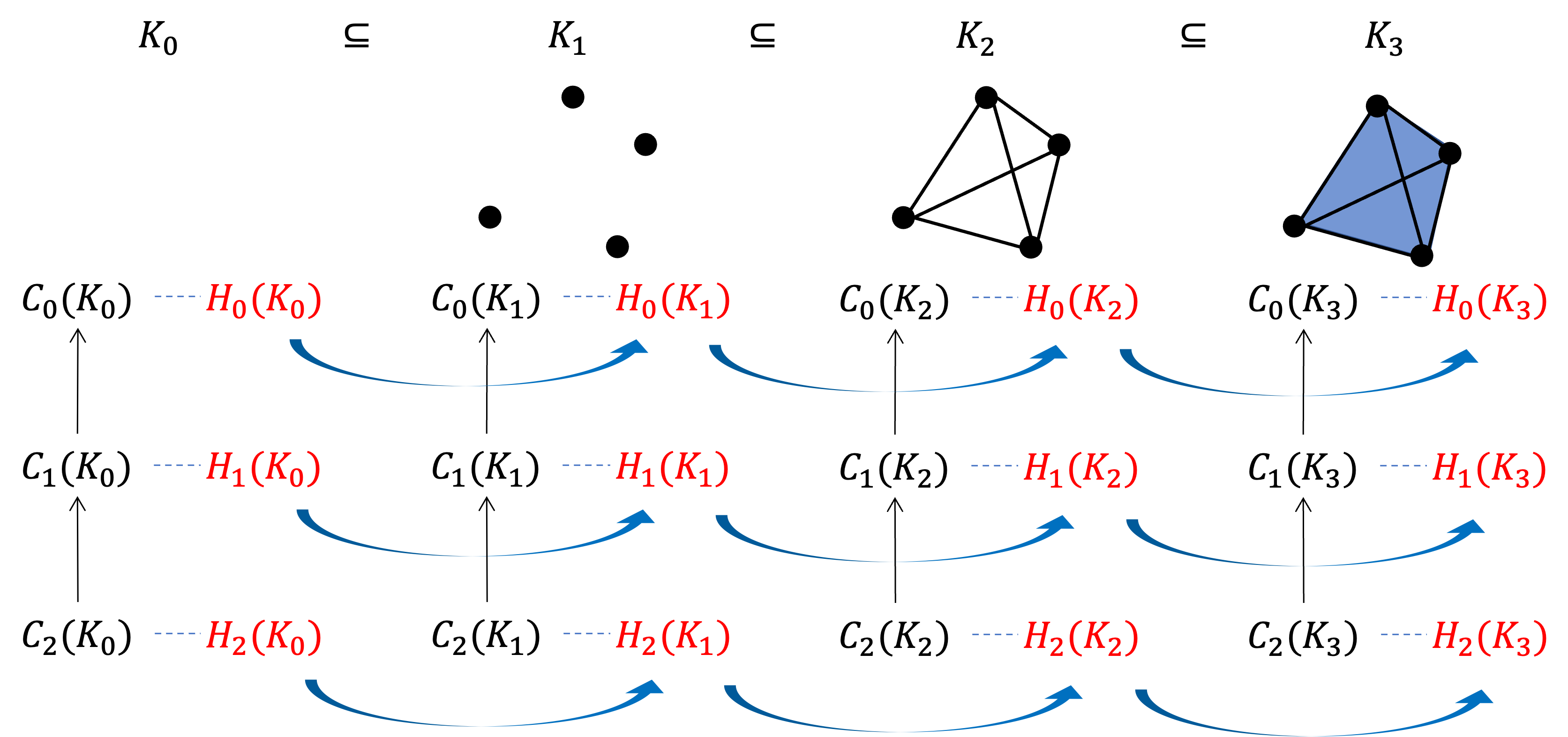
이 자연스러움을 아래의 그림처럼 도식화하곤 합니다.

위 그림에서 각 가로줄은 심플리셜 컴플렉스와 포함관계를 왼쪽에서 오른쪽으로 향하는 화살표 (→)로 연결한 나열, 호몰로지와 포함관계로부터 유도된 선형변환을 왼쪽에서 오른쪽으로 향하는 화살표(→)로 연결한 나열을 나타냅니다.
위에서 아래로 향하는 화살표(↓)는 심플리셜 컴플렉스 $K_i$의 정보를 자연스럽게 호몰로지 $H_k(K_i)$로 대응시켜주는 변환을 나타냅니다.
이 그림의 특징은 가로로 갔다가 아래로 갔을때(→↓) 얻는 정보와 아래로 먼저 갔다가 가로로 동일하게 갔을때(↓→) 얻는 정보가 완벽하게 일치한다는 점입니다.

이러한 성질로부터 우리가 기존에 알던 필트레이션의 기하학적 정보가 호몰로지로 "자연스럽게" 옮겨졌고, 우리는 이 정보를 믿고 사용할 수 있게 됩니다.

어찌저찌 우리는 우리가 원하던 기하학적 정보의 변화를 담고있는 호몰로지들의 나열 $\left\{H_k(K_i)\right\}_{i=0}^n$과 이들을 연결해주는 선형변환들 $\left\{f_{a,b}\right\}_{a\leq b}$를 얻었습니다.
이제 정말 우리가 원하던 지속성 호몰로지를 정의할 준비가 끝났습니다.

---

📝 요약 Summary

• 필트레이션을 구성하는 각각의 서브컴플렉스들의 호몰로지들을 연결해줘야 기하학적 정보의 변화를 계산할 수 있다.
• 심플리셜 컴플렉스들의 카테고리와 호몰로지들의 카테고리 사이에 자연스러운 변환이 존재한다.
• 이 자연스러운 변환에 의해 호몰로지의 변화관계를 얻는다.