본 포스팅 시리즈는 다양한 머신러닝 테크닉에 대해 수학적 관점과 실용적 관점에서 정리한다.
필자는 수학을 전공했기 때문에 수학적 접근과 용어에 대해 익숙하게 사용한 것이 있지만, 수학을 전공하지 않은 사람들에겐 다소 낯선 접근과 용어가 있을 수 있다.
최대한 그러한 부분을 자세히 설명하려 노력하였지만 필자의 타전공자에 대한 '공감능력부족'으로 효과적으로 전달되지 못한 부분이 있을 것으로 생각된다.
이 글을 읽어주시는 분께 일차적으로 감사드리며, 해당 부분에 대해 질문이나 코멘트를 남겨주시는 분께는 거듭제곱으로 감사드림을 말씀드린다.
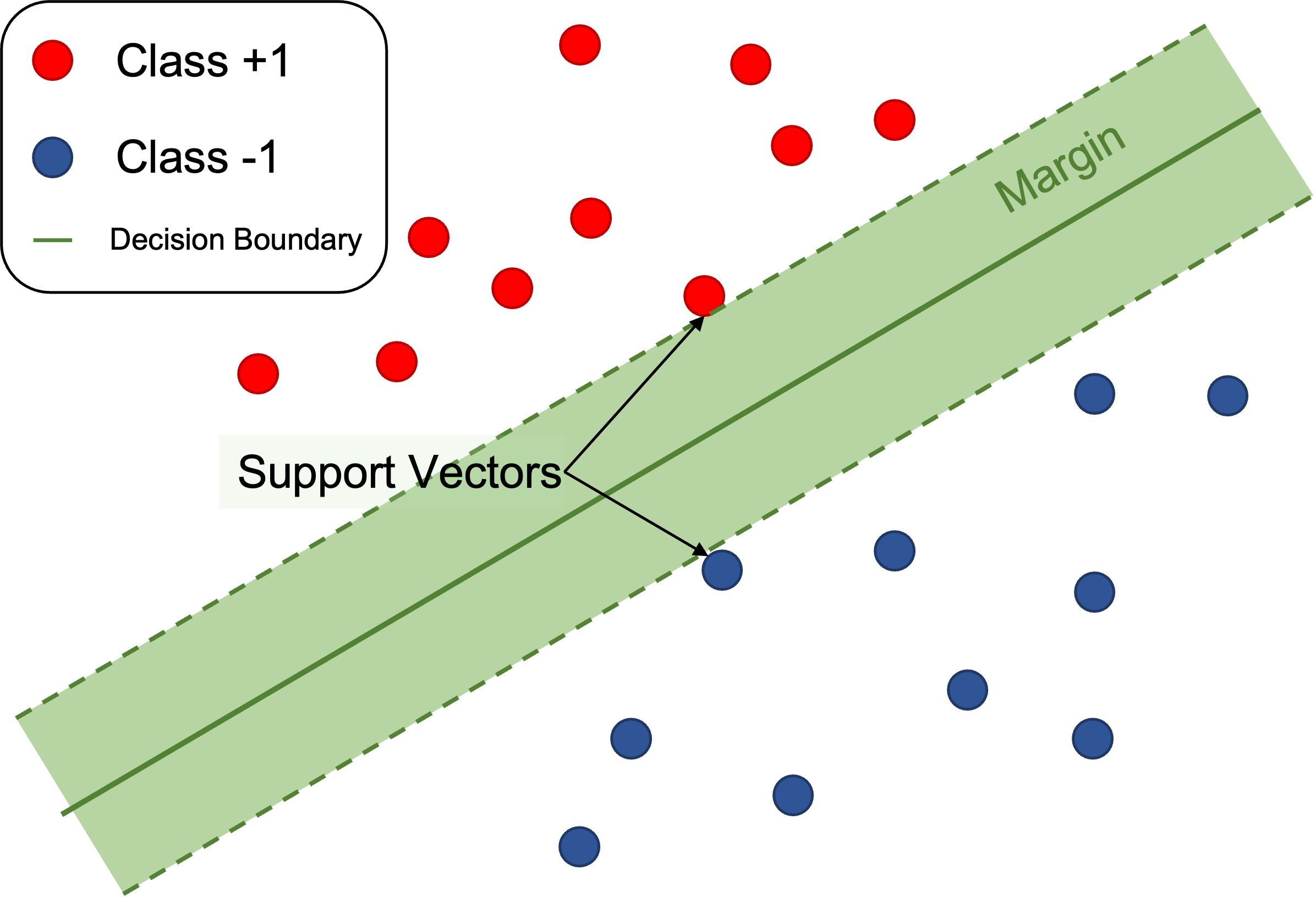
Support Vector Machine
서포트 벡터 머신은 딥러닝이 등장하기 이전에 가장 유명하고 성능 좋은 머신러닝 모델이었다고 한다.
현재는 다소 실무에서 사용되는 정도가 줄어들었겠지만, 서포트 벡터 머신에 적용되는 다양한 수학적 테크닉들은 인공지능을 이해하고 연구하는 데에 여전히 훌륭한 인사이트를 준다고 생각한다.
특히 서포트 벡터 머신의 아이디어는 유클리드 기하학과 최적화 이론으로 설명이 된다는 점은 수학자들에게 있어서 굉장히 매력적이다.
본 포스팅의 내용은 다음의 자료들을 참고했다.
- Mathematics for Machine Learning (Deisenroth, Marc Peter and Faisal, A. Aldo and Ong, Cheng Soon)
- The Elements for Statistical Learning (Trevor Hastie, Robert Tibshirani, Jerome Friedman)
- 김민준님(이화여자대학교, 수학과 석사)의 SVM Lecture note
- 김원화 교수님(포항공과대학교, 인공지능대학원 교수)의 데이터 마이닝 Lecture note
- Hands-On Machine Learning with Scikit-Learn, Keras, and Tensorflow (Aurelien, Geron)
6. Soft-margin SVM (1)
지금까지 살펴봤던 하드마진 SVM은 현실적으로 좋은 성능을 내기 어렵다.
현실의 데이터는 노이즈나 이상치가 많고 이런 샘플의 존재는 마진이 굉장히 작아질 수 밖에 없도록 강제하기도 한다.

이런 점에서 하드마진 SVM은 이상치에 민감하다고 할 수 있다.
더욱 심한 경우는 데이터가 선형분류가 불가능한 경우다.

위 그림과 같이 파란 샘플의 군집에 속한 단 하나의 빨간 샘플에 의해 선형분류가 불가능해질 수 있다.
그리고 불행하게도 이러한 일은 현실에서 매우 흔하게 일어난다.
6.1 잉여인간도 쓸모가 있다
영화 말죽거리 잔혹사에서 잉여인간이라는 용어가 등장했다. "너, 대학 못가면 뭔 줄 알아? 잉여인간이야, 잉여인간!"
(영상출처 :유튜브 채널 Ailenschzar)
필자가 어린 시절에 인터넷에서는 잉여 또는 잉여인간이라는 말이 인터넷에 유행했었다.
현실에선 하릴없이 배나 긁으면서 하루종일 인터넷 커뮤니티에서 온종일 시간을 떼우는 사람들을 지칭하거나 스스로를 자조하는 용어였다.
옛날엔 잉여에 대한 취급이 참 많이 박했다.
오직 열심히 최선을 다해 무언가 배우고 생산하는 활동만이 유용하다고 여겨졌다.
그러나 요즘에 유튜브와 같은 소셜 네트워크 서비스가 발달하면서 잉여로운 컨텐츠들이 사람들에게 인기를 얻고 있다.
요즘 사람들이 자신의 삶에 잉여로운 시간들을 얼마나 소중하게 여기는지 생각해보라.
워라벨이라는 키워드가 한창 많은 사람들이 열광하는 가치관으로 떠오르더니 이젠 스타벅스가 딸린 건물주가 되어서 딱히 열정 없이 잉여롭게 살지만 부족하지는 않은 삶을 꿈꾸고 있다.
우리는 잉여가 쓸모있는 시대, 잉여인간이 되길 꿈꾸는 시대에 살고있다.
SVM 이야기를 하다가 왜 갑자기 잉여에 대한 이야기를 하냐면, 이 잉여(slack)의 개념이 SVM의 한계를 극복할 강력한 무기가 되기 때문이다.
하드 마진 SVM이 마진의 잉여에 대해 조금의 융통성도 허락하지 않았지만, 이번 포스팅에서 학습할 소프트 마진 SVM(Soft-margin SVM)은 마진에 잉여를 허가해줌으로써 하드 마진 SVM이 가지고 있던 한계를 극복한다.
6.2 소프트 마진 SVM의 정의 : 기하학적 관점

그림과 같이 훈련 데이터의 클래스가 다소 섞여있다고 하자.
소프트 마진 SVM은 결정경계를 여전히 선형경계로 택하되, 마진의 폭 내부에 어느 정도 오차가 들어와도 용인해주도록 융통성을 부여해 일반화 성능의 향상을 기대할 수 있도록 한다.
하드 마진 SVM의 경우 훈련 데이터가 선형분류가 가능하다는 가정을 상당히 신뢰하였다.
그러나 소프트 마진 SVM은 현실적으로 훈련 데이터가 완전하지 못하며, 이상치나 노이즈가 있을 수 있을 수 있다는 점에 오히려 더 무게를 둔다.
그러므로 결정 경계의 근방에서 발생할 노이즈나 이상치 데이터는 조금 틀리도록 여유를 두면서 훨씬 더 많은 정상치 데이터는 최대한 잘 분류할 수 있도록 넓은 마진을 가지는 선형경계를 만든다.
핵심 아이디어는 각 훈련 데이터 샘플 마다 잉여 변수(slack variable) 를 대응시켜서 샘플이 마진의 폭 안으로 만큼 파고드는 상황(심하게는 결정경계 건너편으로 넘어가 오답이 되는 상황)을 용인해주는 것이다.

이는 각 샘플 의 제약조건을 로 변형하는 것으로 구현된다.
아무리 잉여가 좋다고 해도, 구성원 모두가 잉여가 되어버리면 그 사회는 무너질게 뻔하다.
매정하지만, 잉여는 선택받은 소수만 누릴 수 있도록 잉여의 총합은 최소가 되도록 해야할 것이다.
소프트 마진 SVM은 이러한 생각을 반영하여 다음과 같이 마진 최적화 문제를 변형한 것이다.
여기서 하이퍼 파라미터 는 마진의 폭과 잉여의 총합 간의 trade-off를 조정하는 규제 파라미터(regularization parameter) 또는 페널티(Penalty)다.
만약 라면 소프트 마진 SVM은 샘플 을 잘못 분류되게 된다.
값은 모델이 오답을 낼때마다 벌칙을 얼마나 더 강하게 부여할지 결정한다.
모델은 의 값을 최소화하고 싶은데 값이 크다면 오답을 낼수록 목적함수를 최소화하기가 더욱 어려워지기 때문에 를 벌칙(페널티)이라 명명한 것은 적절해보인다.
페널티에 대해서는 다음에 더 자세히 알아보도록 하자.
이번 포스팅에서는 하드 마진 SVM의 한계를 극복하기 위해 도입된 소프트 마진 SVM을 소개하고, 기하학적 관점에서 잉여 변수를 정의하고 모델을 해석해보았다.
다음 포스팅에서는 잉여가 쓸모있다던 필자가 갑자기 말을 바꾸어, 잉여는 결국 손실이라는 관점에서 소프트 마진 SVM을 도입해볼 것이다.
