교육 정보
- 교육 명: 경기미래기술학교 AI 교육
- 교육 기간: 2023.05.08 ~ 2023.10.31
- 오늘의 커리큘럼: 빅데이터 기초 활용 역량 강화 (5/10~6/9) - 데이터 분석
- 강사: 조미정 강사님 (빅데이터, 머신러닝, 인공지능)
- 강의 계획:
1. 파이썬 언어 기초 프로그래밍
2. 크롤링 - 데이터 분석을 위한 데이터 수집(파이썬으로 진행)
3. 탐색적 데이터 분석, 분석 실습
- 분석은 파이썬만으로는 할 수 없으므로 분석 라이브러리/시각화 라이브러리를 통해 분석
4. 통계기반 데이터 분석
5. 미니프로젝트
통계 분석 방법
중심 극한 정리
import matplotlib.pyplot as plt
import numpy as np
import random
# 모집단 갯수 range(1,100000)
# 표본의 크기 100
# 시행횟수 5000번
# 평균의 위치, 분산의 모양 파악
avg_values = []
for i in range(1,5001):
random_sample = random.sample(range(1,100000),100)
x_bar = np.mean(random_sample)
avg_values.append(x_bar)
plt.hist(avg_values,bins = 100)
plt.show()
# 표본수가 100일때와 30일때, 10일때를 비교해보면 표본이 적을수록 더 퍼져있음
# -> 표본 평균은 모집단의 평균을 따른다.
# -> 샘플이 많을수록 분산이 좁음 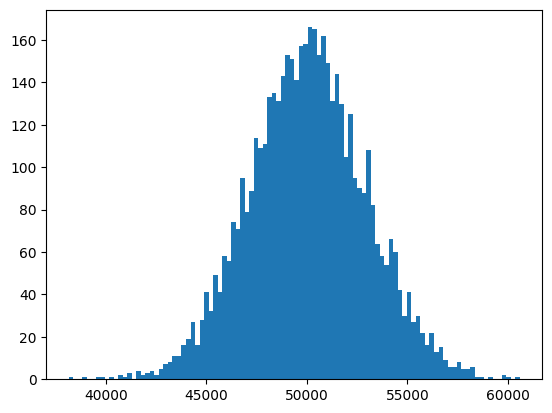
t 검정
- 집단 간 평균 차이 검정
One Sample t-test (단일표본 t 검정)
표본이 하나일 때, 모집단의 평균과 표본집단의 평균 사이에 차이가 있는지를 검증하는 방법
scipy.stats 의 ttest_1samp(a, popman) 이용
import pandas as pd
from scipy import stats
bus = pd.read_csv('/content/bus_wait_time.csv')
bus
# h0: 뮤 =15 (귀무가설, 버스회사의 주장)
# h1: 뮤 !=15 ()
# 표본이 하나고 모집단의 평균과 표본집단의 평균 차이 검정
t_value, p_value = stats.ttest_1samp(bus['waittime'],popmean = 15) # pop = poplulartion = 모집단
#statistic = 0.05, p value 는 0.95(95%)
print("t 값: ", round(t_value, 4), "p 값: ", round(p_value, 4))
#
#결과
t 값: 0.0588 p 값: 0.9531결과 해석
- t는 목표와 얼마나 떨어져있는지를 의미, 클수록 귀무가설과 거리가 있다는 것
- 결론적으로 위 셀에서 실행한 값을 보면 p value가 유의 수준 0.05보다 크므로 귀무가설을 기각할수 없다
- 귀무가설을 채택한다.
- 따라서 버스 배차 시간은 15분이라고 할수 있다.
Two Sample t-test(독립표본 t검정)
서로 다른 두 개의 그룹 간 평균 검정을 위한 방법
scipy.stats 의 ttest_ind(x, y) 함수 이용
'새로운 강의 방식이 학생들의 독해력 향상에 도움을 주는가?'
새로운 강의 방식에 의한 평균이 기존의 강의방식에 의한 평균보다 큰지 검정
16명의 학생들을 8명씩 랜덤 추출하여 두집단으로 나눔
한 집단에는 기존 방식(old), 한 집단에는 새로운 방식(new)
H0 : u1 = u2 , H1: u1 > u2
import pandas as pd
reading = pd.read_csv('Reading.csv')
reading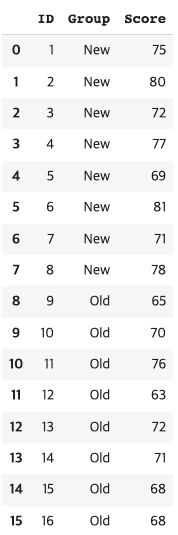
new 그룹과 old 그룹의 점수 비교
h0: new 평균 == old평균 혹은 (new평균-old평균) == 0
h1: new 평균 != old평균
import seaborn as sns
sns.boxplot (data = reading, x= 'Group', y = 'Score')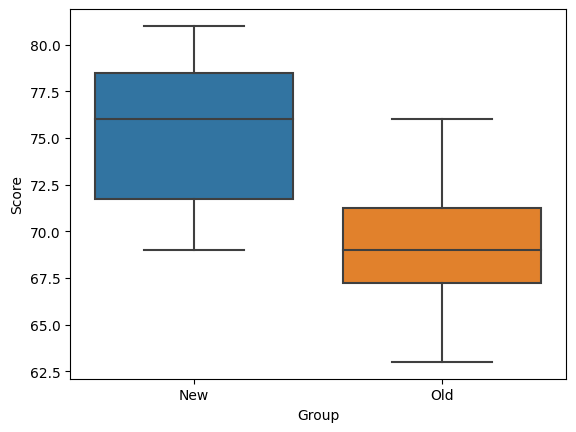
# 집단 나누기
new = reading[reading.Group == 'New']
old = reading[reading.Group == 'Old']
# 칼럼 이름은 .으로도 불러올수 있어서 reading.Group == 'New'이 뒷 문장과 같은 역할 new = reading[Group] == 'New'
# ttest_ind
stat,pval = stats.ttest_ind(new.Score, old.Score) # 등분산 가정, 양측 검정
# 양측 검정과 편측 검정이 있는데 기본은 양측 검정이고 옵션을 줘서 편측으로 바꿀 수 있음
print(stat, pval)
#
#결과
2.9536127902039953 0.010470744188033123결과해석
- 유의수준 0.05하에 P value가 유의수준보다 작음 (귀무가설의 그래프의 끝단에 있다는것) -> 귀무가설 기각
- 즉, new 평균과 old 평균은 차이를 가진다고 할 수 있다.
- 즉 새로운 강의 방식은 학생들의 점수에 영향이 있다고 할 수 있다.
Paired t-test(대응표본 t검정)
연관된 두 집단의 차이 에 대한 단일 표본의 평균 검정을 진행하는 방법 (교육 전후의 점수 차이 등)
scipy.stats 의 ttest_rel(x, y)
실험 단위를 동질적인 쌍으로 묶은 다음 각 쌍에 대해 랜덤하게 두 처리를 적용하고, 각 쌍에서 얻어진 반응 값의 차이를 이용하여 두 모평균 비교
대응표본 t- 검정사례
'컴퓨터 교육 실시하기 전과 후의 성적 차이가 있는가?'
15명의 학생에게 통계학 시험 성적 전후 비교
paired = pd.read_csv('Paired.csv')
paired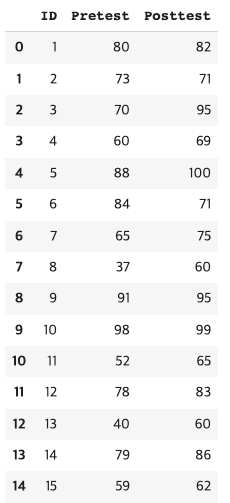
# h0 = pretest평균 == posttest 평균 (즉 pretest평균 - posttest 평균 == 0 )
# h1 = pretest평균 < posttest 평균 (즉 pretest평균 - posttest 평균 < 0 )
# stats.ttest_rel
stat, pval = stats.ttest_rel(paired.Pretest, paired.Posttest, alternative = 'less')
print(stat, pval)
#
#결과
-3.093705670004429 0.003965461614513267결과 해석
- 유의 수준 0.05 하의 유의 확률(pval)이 0.0039로 유의수준보다 작으므로 h0기각
- 즉 pretest 평균이 posttest 평균보다 작다고 할수 있다.
- 즉 컴퓨터 교육은 통계학 시험에 영향을 준다고 할수 있다.
카이제곱 독립성 검정
범주형 자료
- 서로 연관성이 있는가? (독립적인가?)
- scipy.stats 의 chi2_contingency() 함수 이용
2차원 교차표(분할표) 작성 - Prefer 데이터
import pandas as pd
Prefer = pd.read_csv('/content/Prefer.csv')
Prefer
# agegroup이 행 product가 열인 형태로 만들어줘야 함 -> pd.crosstab 분할표 생성
print(Prefer.Agegroup.unique())
print(Prefer.Product.unique())
#
#결과
['30<' '30>=']
['B' 'A' 'C']# pd.crosstab (분할표 생성)
Prefer_table = pd.crosstab(index = Prefer.Agegroup, columns= Prefer.Product)
print(Prefer_table)
pd.crosstab(index = Prefer.Agegroup, columns= Prefer.Product, margins=True) # margins = True이면 각 행과 열의 합계가 생성됨 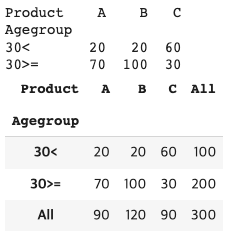
# h0: (분할표의 행과 열이) 독립적이다 /연관성이 없다. 관측빈도 = 기대빈도
# h1: 독립적이지 않다 / 연관성이 있다. 관측빈도 != 기대빈도
# stats.chi2_contingency( ) 입력값으로 분할표를 넣음
stats.chi2_contingency(Prefer_table)
# pvalue
# dof 자유도
# 기대빈도
#
#결과
Chi2ContingencyResult(statistic=65.0, pvalue=7.681204685202098e-15, dof=2, expected_freq=array([[30., 40., 30.],
[60., 80., 60.]]))결과해석
- 유의 수준 0.05하에 p value가 0이므로 0.05보다 작아서 귀무가설 기각
- 따라서 Agegroup과 상품의 구매는 연관성이 있다.
상관 분석
import pandas as pd
import warnings
warnings.filterwarnings("ignore")
student=pd.read_csv('/content/Student.csv')
student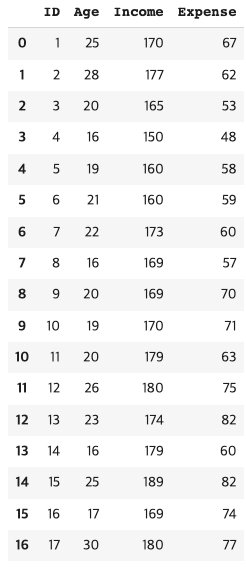
# 상관관계를 확인하기 위해 산점도- 산관계수를 확인
# 산점도
sns.scatterplot(data = student, x= 'Income', y = 'Expense')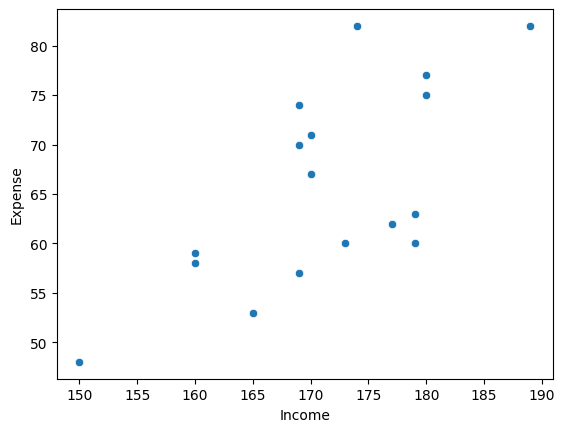
sns.regplot(data = student, x= 'Income', y = 'Expense')
# 관계가 있어보임 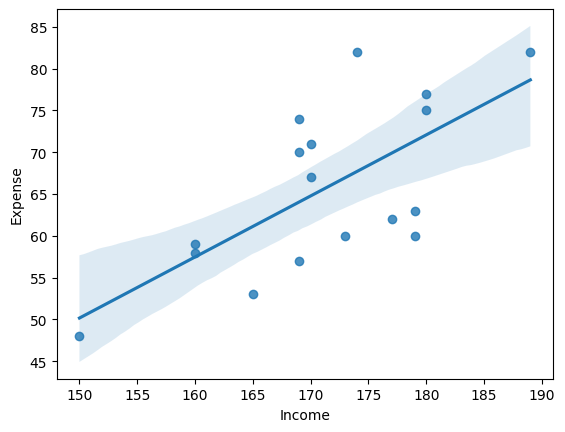
student.corr() # defalut -> method = 'pearson'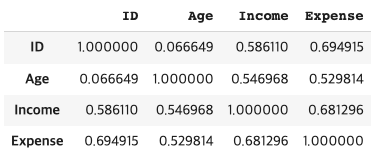
sns.heatmap(student.corr(method = 'pearson'), annot= True, cmap = 'binary')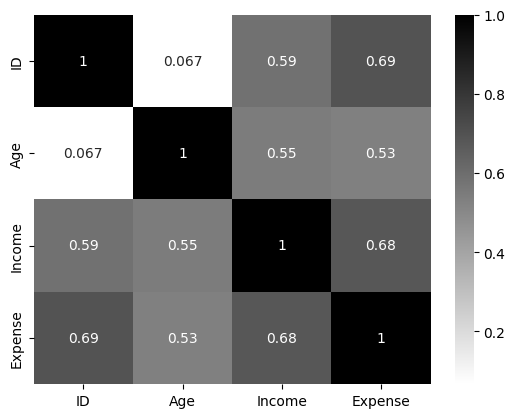
# 상관계수에 대한 검정
# h0: 상관계수 == 0
# h1: 상관계수 != 0
# stats.pearsonr
stats.pearsonr(student.Income, student.Expense)
#
#결과
PearsonRResult(statistic=0.6812956535794541, pvalue=0.0026006496946941993)결과 해석
- 유의 수준 0.05하의 pvalue 가 0.002로 유의수준보다 작으므로 귀무가설 기각
- 즉 상관계수는 0이 아니다. 즉 상관계수 0.68은 유의하다.
