교육 정보
- 교육 명: 경기미래기술학교 AI 교육
- 교육 기간: 2023.05.08 ~ 2023.10.31
- 오늘의 커리큘럼:
파이썬 기반의 머신러닝 이해와 실습 (06/14~07/07)- 강사: 양정은 강사님
- 강의 계획:
1. 개발환경세팅 - IDE, 가상환경
2. 인공지능을 위한 Python
3. KNN 구현을 위한 NumPy
4. K Nearest Neighbors Classification 구현
5. K Means Clustering Mini-project
6. Scikit-learn을 이용한 SVM의 학습
7. Decision Tree의 개념
8. ID3 Algorithm
9. Impurity Metrics - Information Gain Ratio, Gini Index
10. Decision Tree 구현
11. 확률 기초
12. Bayes 정리 예시
13. Naive Bayes Classifier
14. Gaussian Naive Bayes Classifier
Gaussian Naive Bayes Classifier
- Continuous value를 가지는 데이터를 처리하기 위해 정규분포를 도입한 Bayes Classifier
- 정확한 연산이 아니라 어떤 값이 어떤 class에 속할 확률이 높은지 비교하는게 목적 - 완벽한 수학적 정의를 따르지 않음
- 데이터가 정규분포를 따른다고 '가정'
- 확률밀도를 likelihood로 '가정'
GaussianNaive Bayes Classifier
정규분포의 특징
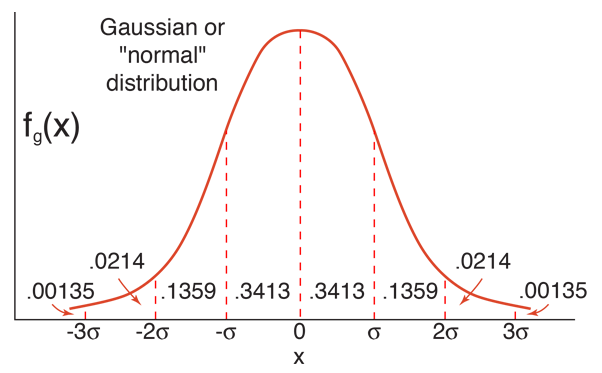
- 정규분포 식을 따름
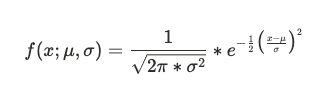
→ 여기서 f(x)는 확률 밀도 값
왜 f(x)가 확률이 아니라 확률 밀도인가?
- continuous 값은 특정 값이 있을 확률을 계산할 수 있는게 아니므로 μ을 기준으로 x사이에 데이터가 들어갈 확률, 확률 밀도를 계산하게 되는것
- 어떤 값x를 정규분포에 넣었을때 계산되는 f(x)값을 바로 likelihood로 사용할 수 있음
- 확률 밀도를 likelihood로 가정하는것부터 완벽한 수학적 정의에서는 벗어난것
→ 비교를 목적으로 연산의 간편화를 위해서 정규분포의 확률밀도값을 likelihood로 사용
→ f(x) = 확률 밀도 / 확률 밀도의 적분 = 확률
- Bell shape
- mean(μ)을 기준으로 좌우대칭
- mean(μ)±nSTD(nσ)를 기준으로 확률 분포를 알 수 있음
Gaussian Naive Bayes Classifier의 동작 원리
- 각각의 데이터에서 μ, σ를 계산해서 정규분포 그래프를 그림
- 특정값(x)을 정규분포 식에 넣어서 f(x) 즉 확률 밀도를 구함
- 확률밀도를 likelihood로 사용해 posterior 계산
예시
def make_gaussian(x, mean, std):
const = 1/np.sqrt(2*np.pi*std**2)
numerator = (x - mean)**2
denominator = 2*std**2
exp_term = np.exp(-numerator/denominator)
y = const * exp_term
return y
⋮
new_data = -0.5
prior0 = n_class0_data / n_total_data
likelihood0 = make_gaussian(new_data, mean0, std0)
posterior0 = prior0 * likelihood0
prior1 = n_class1_data / n_total_data
likelihood1 = make_gaussian(new_data, mean1, std1)
posterior1 = prior1 * likelihood1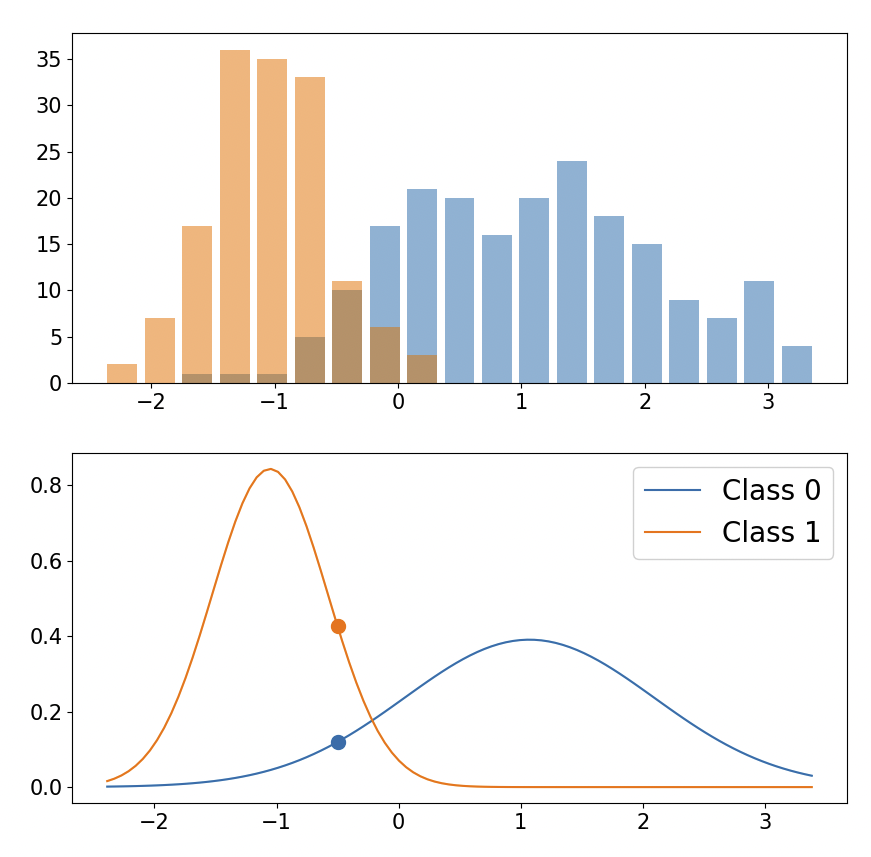
Gaussian Naive Bayes Classifier 적용
- iris data에 Gaussian Naive Bayes Classifier 적용해 본 결과
- posterior = 모든 feature의 likelihood의 곱 * Prior
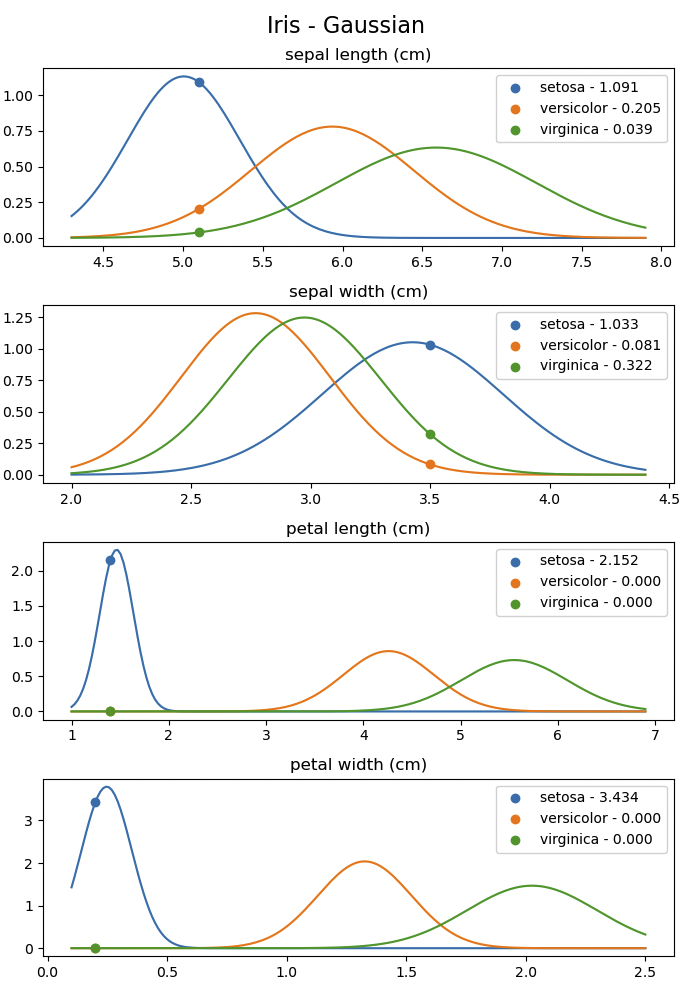
기타 사항 노션에 백업함
