딥러닝 Deep learning - Artificial Neuron(2)

LSH·2023년 9월 1일
0

경기미래기술학교 AI과정 _ TIL

목록 보기
66/72

교육 정보

  • 교육 명: 경기미래기술학교 AI 교육
  • 교육 기간: 2023.05.08 ~ 2023.10.31
  • 강사: 양정은 강사님
  • 강의 계획:
    1. 딥러닝 소개 및 프레임워크 설치
    2. Artificial Neurons Multilayer Perceptrons
    3. 미분 기초 Backpropagation
    4. MLP 구현하기
    5. MLP로 MNIST 학습시키기(Mini-project)
    6. Sobel Filtering
    7. Convolutional Layers
    8. 이미지 분류를 위한 CNNs
    9. CNN으로 MNIST 학습시키기
    10. VGGNet, ResNet, GoogLeNet
    11. Image Classification 미니 프로젝트
    12. Object Detection 소개
    13. Region Proposal, Selective Search
    14. RCNN
    15. Single Shot Detection

Artificial Neuron

  • Artificial Neuron Class로 만들어 사용
    ✏️ 주의할 점
  • 처음에는 클래스 중첩을 사용하려 했었음
    • 종속 관계가 아니므로 X
  • 데이터 x 값을 ArtificialNeuron의 __init__에 넘김
    • 같은 함수에 많은 데이터를 학습시키므로 method에 넣어야함
      → 특성을 잘 생각하고 설계하기
  • 연산 method 내에서 affine, activation function 정의
    → 한번 연산 할 때마다 초기화 → 학습이 안 됨

Neuron Class를 사용한 다른 Class 생성

class Example:
    def __init__(self):
        self.EX = ArtificialNeuron(w=[5, 5], b=-7.5)
        # 사용할 함수(gate 등) 구현 

    def forward(self, x1, x2):
        #init에서 정의한 함수를 사용한 연산

MultiLayer Perceptron (MLP)

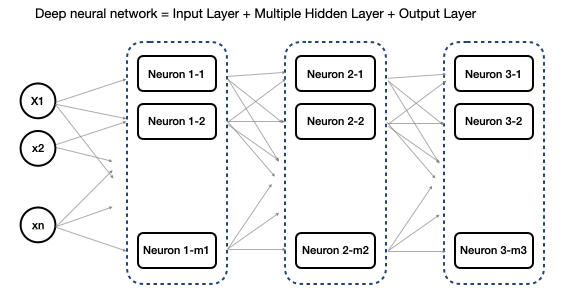
  • 여러개의 입력값이 한 층에 있는 여러개의 뉴런들에 각각 들어가서 서로 다른 패턴을 추출하여 결과를 출력 → 다음 층의 레이어에 있는 뉴런들에 입력됨 이렇게 레이어가 깊어질수록 복잡한 패턴을 추출한다고 볼 수 있음
  • Deep neural network = Input Layer + Multiple Hidden Layer + Output Layer
  • 이전 뉴런의 w(weight, 가중치)는 들어온 데이터의 중요도를 판단하는데 어느정도 영향을 가지는지를 나타냄
    • 어떤 뉴런의 w = 0: 해당 뉴런이 해당 데이터의 중요도를 전혀 판별하지 못함을 의미

한 레이어의 뉴런들은 n개의 데이터를 받을때 n개의 w를 가지게 되고 뉴런의 갯수가 m개라고 하면 전체 w의 갯수는 nm행렬이 됨 여기에 m개의 뉴런이 각 한개의 b를 가지므로b는 m크기의 scalar
그러므로 총 파마리터의 갯수는 mn + m1 = m(n+1)개
→ 모델내의 전체 파라미터의 갯수가 딥러닝 모델의 복잡도를 결정함

w*x+b를 하기 위해서 행렬인 w와 x (종종 b도)를 transpose, 행렬전환 해야 할수 있음 → 자유자재로 할 수 있어야 함


MLP의 입출력 기본

입력 X는 보통 행렬로 들어옴 (일단 bias 제외)
→ 필요하다면 broadcating이 가능한 형태로 Transpose 해야함

[⟵x(1)⟶⟵x(2)⟶⋮⟵x(n)⟶][↑↑↑w1w2…wn↓↓↓]\begin{bmatrix} \longleftarrow x^{(1)}\longrightarrow \\ \longleftarrow x^{(2)}\longrightarrow \\ \vdots\\ \longleftarrow x^{(n)}\longrightarrow\\ \end{bmatrix} \begin{bmatrix} \big\uparrow &\big\uparrow &&\big\uparrow \\ w_{1} & w_{2} & \dots & w_{n} \\ \big\downarrow &\big\downarrow &&\big\downarrow \\ \end{bmatrix}

이때 출력 값은 아래와 같음

Z=[x(1)w1x(1)w2…x(1)wnx(2)w1x(2)w2…x(2)wn⋮⋮⋱⋮x(n)w1x(n)w2…x(n)wn]\bold{Z} = \begin{bmatrix} x^{(1)}w_{1} & x^{(1)}w_{2} & \dots & x^{(1)}w_{n} \\ x^{(2)}w_{1} & x^{(2)}w_{2} & \dots & x^{(2)}w_{n} \\ \vdots & \vdots & \ddots & \vdots \\ x^{(n)}w_{1} & x^{(n)}w_{2} & \dots & x^{(n)}w_{n} \\ \end{bmatrix}

Z 의 각 원소들의 표현/의미

  • [Z]ij[Z]_{ij}
    • i번째 데이터가 j번째 뉴런을 통과했을때의 affine value
  • [Z]i[Z]_{i}
    • i번째 데이터가 모든 뉴런을 통과했을때의 affine value
    • 이 모델에서의 학습 결과에 대한 i번째 데이터의 중요도
  • [Z]j[Z]_{j}
    • 모든 데이터가 j번째 뉴런을 통과했을때의 affine value
    • j번째 뉴런이 이 데이터셋의 중요도를 측정하는데 가지는 영향력

Z 값이 Activation 함수까지 지나면 아래와 같이 표현함 (시그모이드σ\sigma 사용하여 표현)

A=[σ(x(1)w1)σ(x(1)w2)…σ(x(1)wn)σ(x(2)w1)σ(x(2)w2)…σ(x(2)wn)⋮⋮⋱⋮σ(x(n)w1)σ(x(n)w2)…σ(x(n)wn)]\bold{A} = \begin{bmatrix} \sigma(x^{(1)}w_{1}) & \sigma(x^{(1)}w_{2}) & \dots & \sigma(x^{(1)}w_{n}) \\ \sigma(x^{(2)}w_{1}) & \sigma(x^{(2)}w_{2}) & \dots & \sigma(x^{(2)}w_{n}) \\ \vdots & \vdots & \ddots & \vdots \\ \sigma(x^{(n)}w_{1}) & \sigma(x^{(n)}w_{2}) & \dots & \sigma(x^{(n)}w_{n}) \\ \end{bmatrix}
profile
LSH
:D
이전 포스트

파이썬 클래스 미니 프로젝트 - 게임 만들기

다음 포스트

딥러닝 Deep learning - Loss Functions

0개의 댓글