딥러닝 Deep learning - Loss Functions

LSH·2023년 9월 4일
0

경기미래기술학교 AI과정 _ TIL

목록 보기
67/72

교육 정보

  • 교육 명: 경기미래기술학교 AI 교육
  • 교육 기간: 2023.05.08 ~ 2023.10.31
  • 강사: 양정은 강사님
  • 강의 계획:
    1. 딥러닝 소개 및 프레임워크 설치
    2. Artificial Neurons Multilayer Perceptrons
    3. 미분 기초 Backpropagation
    4. MLP 구현하기
    5. MLP로 MNIST 학습시키기(Mini-project)
    6. Sobel Filtering
    7. Convolutional Layers
    8. 이미지 분류를 위한 CNNs
    9. CNN으로 MNIST 학습시키기
    10. VGGNet, ResNet, GoogLeNet
    11. Image Classification 미니 프로젝트
    12. Object Detection 소개
    13. Region Proposal, Selective Search
    14. RCNN
    15. Single Shot Detection

Loss Functions

Loss Functions

  • 딥러닝 모델이 binary classification 일때 데이터 X가 입력되면 예측값 y^\hat y는

    y^∈(0,1)\hat y \in (0, 1) (확률 값)

ex) 지문인식, 목소리 인식, 얼굴 인식 -> 사용자가 맞는지 (0, 1)로 판별

  • 참고
    y^∈{0,1}:y=0 or 1y^∈(0,1):0<y<1(범위)y^∈[0,1]:0≤y≤1(범위)\hat y \in \{0, 1\} : y = 0 \, or \, 1 \\ \hat y \in (0, 1) : 0 < y < 1 (범위)\\ \hat y \in [0, 1] : 0 \leq y \leq 1 (범위)
  • Loss = 실제 값과 모델 예측값의 차이
    • Loss Function = Loss를 계산하는 함수
Loss= ∣y^−y ∣Loss =\ | \hat y - y \ |

Binary Classification에서의 Loss

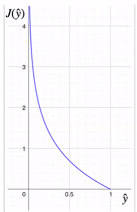
  • 실제값이 0일때 예측값이 0에 가까워질수록 loss는 0에 수렴, 예측값이 1에 까까워 질수록 Loss는 ∞로 발산
J(y^)=−log(y^), 0<y^<1J(\hat y) = -log(\hat y),\, 0 < \hat y <1

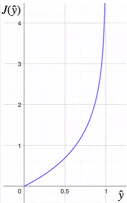
  • 실제값이 1일때 예측값이 1에 가까워질수록 loss는 0에 수렴, 예측값이 0에 까까워 질수록 Loss는 ∞로 발산
J(y^)=−log(1−y^), 0<y^<1J(\hat y) = -log(1-\hat y),\, 0 < \hat y <1

→ 답에 따라 다른 식을 사용해야 하는 불편함이 있음
→ 두 상황 모두 만족할수 있는 식을 찾음
= Binary Cross Entropy
: 정답이 0, 1이고 출력이 확률일때 정답과 출력의 차이를 연산해주는 함수

J(y,y^)=−[y⋅log(y^)+(1−y)log(1−y^)],  0<y^<1J(y, \hat y) = - [y \cdot log(\hat y) + (1 - y)log(1-\hat y)],\,\, 0 < \hat y <1
profile
LSH
:D
이전 포스트

딥러닝 Deep learning - Artificial Neuron(2)

다음 포스트

딥러닝 Deep learning - Modeling

0개의 댓글