양자란

이전 포스트에서 고전 컴퓨터의 방식은 0 아니면 1 인 이분법적 계산으로 이루어져있다는 것을 얘기했었다. 하지만, 양자는 이러한 이분법적 사고와 매우 다르다. 이는 아래의 그림을 보면서 이야기해보려 한다.

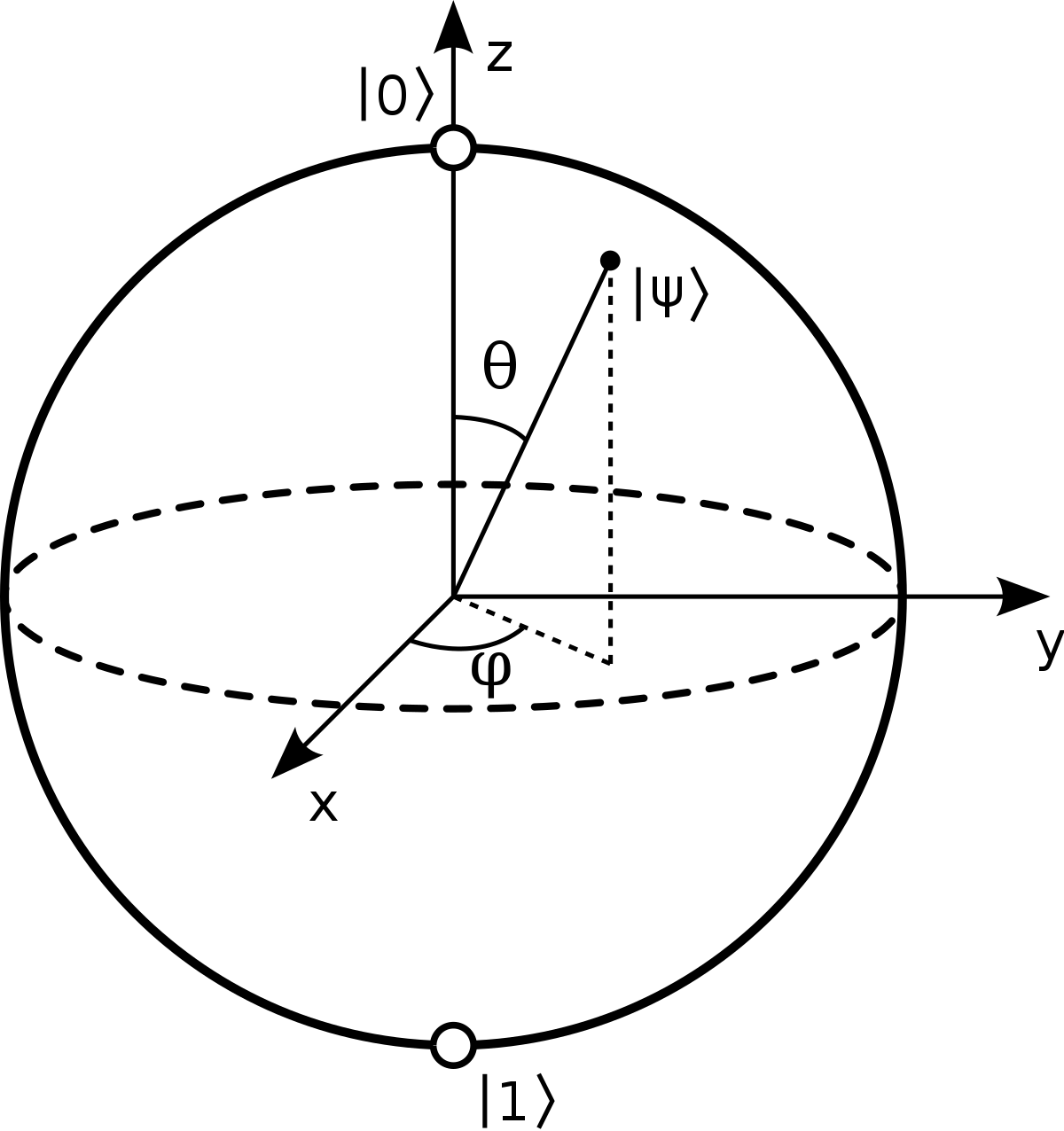
위의 그림은 Bloch Sphere(블로흐 구)라고 불리우며 양자를 기하학적으로 나타낸 것이다. 그림을 자세히 보면 이전 기초 수학 포스트에서 다루었던 Θ가 있는 것으로 보아 Polar Form의 형태로 계산들이 이루어질 것 같은 느낌도 확 온다. 그리고 좌표계의 Z축 상단과 하단을 보면 |0⟩ 과 |1⟩ 이 있다. 상당히 복잡해보이는 그림이지만 우리가 유추할 수 있는 것은 |0⟩과 |1⟩의 양극을 가지는 구면에 있는 점의 좌표를 XY평면의 각도와 XY평면과 Z축과의 각도를 통해 표시한다는 것이다. 수학적으로 표현하면 |0⟩과 |1⟩의 영향을 받아 |𝜓⟩ = 𝛼 |0⟩ + 𝛽 |1⟩ 로 표현된다.

Superposition - 중첩

위에서 말한

|𝜓⟩ = 𝛼 |0⟩ + 𝛽 |1⟩

이 형태가 의미하는 것을 쉽게 설명하자면 하나의 양자는 |0⟩과 |1⟩ 두개의 상태를 동시에 지니고 있다고 볼 수 있다. 대신 주의할 점은 𝛼 와 𝛽 이다. 이 𝛼^2 + 𝛽^2 = 1이다. 즉, 양자는 두 가지 상태를 동시에 가지지만 확률에 기반하여 그 경향성이 정해진다는 것을 의미한다.
이는 아래와 같이 표현되어진다.

50-50 superposition of 0 and 1 : 𝜓⟩ = √0.5|0⟩ + √0.5|1⟩
90-10 superposition of 0 and 1 : 𝜓⟩ = √0.9|0⟩ + √0.1|1⟩

Quantum GATES

Qubit는 양자의 중첩 원리를 활용해 블로흐 구면에서 기하하적으로 표현되어지며 |0⟩과 |1⟩ 두 가지 상태를 가진다는 것을 알았다면 이제는 이 하나의 Qubit들을 연산하는 방법을 알아보자. 이전에 우리느 논리 회로에 대해 얘기한 적이 있다. 이는 고전 컴퓨팅 방식에서 사용되었던 방식이기에 양자 컴퓨터에 활용되는 회로를 추가적으로 알아야 한다.

• X-gate : bit-flip
  
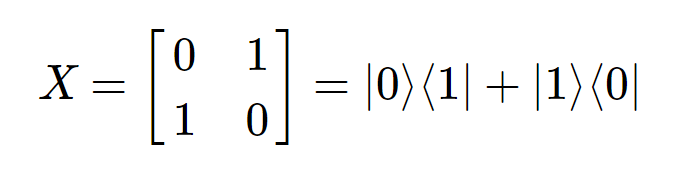
• Y-gate : phase gate
• Hadamrd(H) : creates a 50-50 superposition from |0⟩ and |1⟩
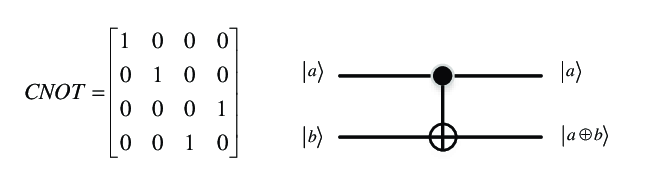
• CNOT-gate: if control qubit is 1, flip the target qubit
  

Quantuam Supremacy - 양자 우월성

To be continued..