기초 수학

이번 내용은 양자 컴퓨팅을 이해하기 위한 기초 수학 편이다.
말 그대로 '기초'이기 때문에 어려운 내용은 딱히 없다(물론, 어려울 수는 있다..)
고등학교 때 배웠던 수학 정도의 수준이니 크게 걱정할 필요는 없을 것 같다.

"필자도 이 분야의 전문가가 아닌 학생이므로 쉬운 내용일 수 밖에..."

그럼 본론으로 들어가보자

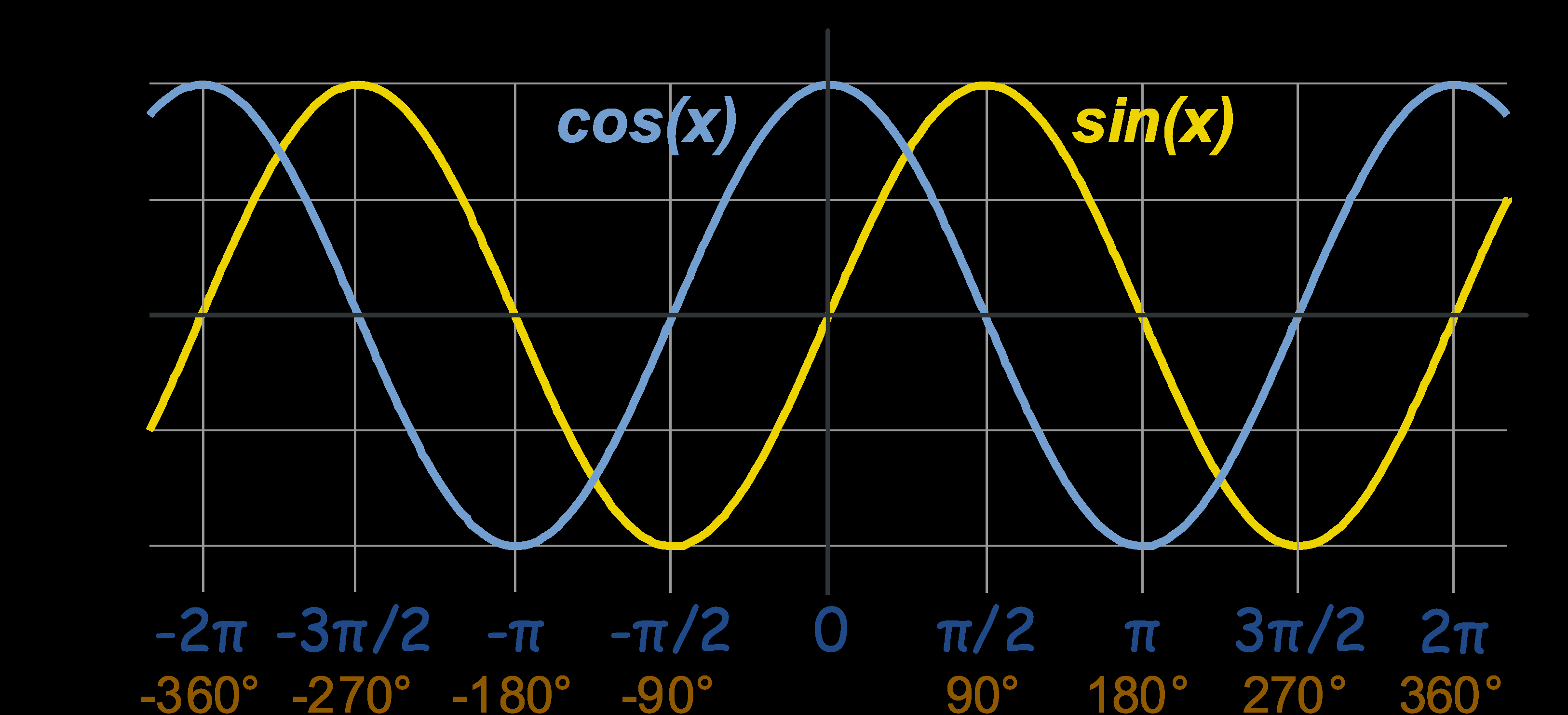
삼각법(Trigonometric)

삼각법이란 우리가 고등학교 때 배웠던 삼각함수라 생각하면 되는데 3 변의 길이와 각도를 활용하는 법을 의미한다. 그리고 이러한 방법을 통해 우리는 일반적인 좌표계에서도 길이와 각도를 구할 수 있다.

Cartesian to Polar

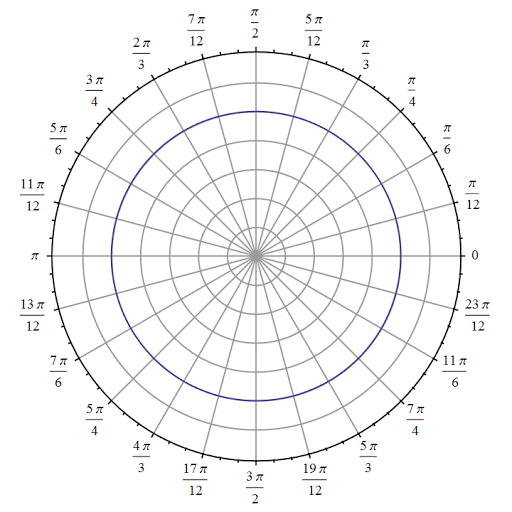
여기서 Cartesian이란 흔히 우리가 알고있는 좌표계로 생각하면 된다. Polar란 극좌표계로 위치를 표현하는 방법이 길이와 방향으로 표기된다.
(X,Y) -> (r,Θ) 과 같이 흔히 우리가 사용하는 x,y 좌표를 반경 r 과 각도 Θ 로 표현하는 방식이 삼각법을 활용하는 것이다. 여기서 우리는 반경은 피타고라스 정리를 통해 알 수 있지만 각도는 어떻게 구해야 하나? 라는 걱정이 생길 수 있다. 그리고 이에 대한 해결법은 탄젠트의 역함수이며 arctan 라 불리운다.

• tanΘ = Y/X
• Θ = arctan(Y/X)

그렇다면 반대로 Polar form 에서 Carteisan Form 으로 변경하는 작업은 아래와 같다

• x = r*cosΘ
• y = r*sinΘ

벡터(Vector)

벡터는 쉽게 말해 방향성을 가진 힘이라 생각하면 된다. 이는 방향성이 없이 오직 힘의 크기만을 의미하는 스칼라와는 반대되는 개념이다.

벡터는 2D 상에서 아래와 같이 행렬로 표기되며 그래프 상에 표현되어진다.

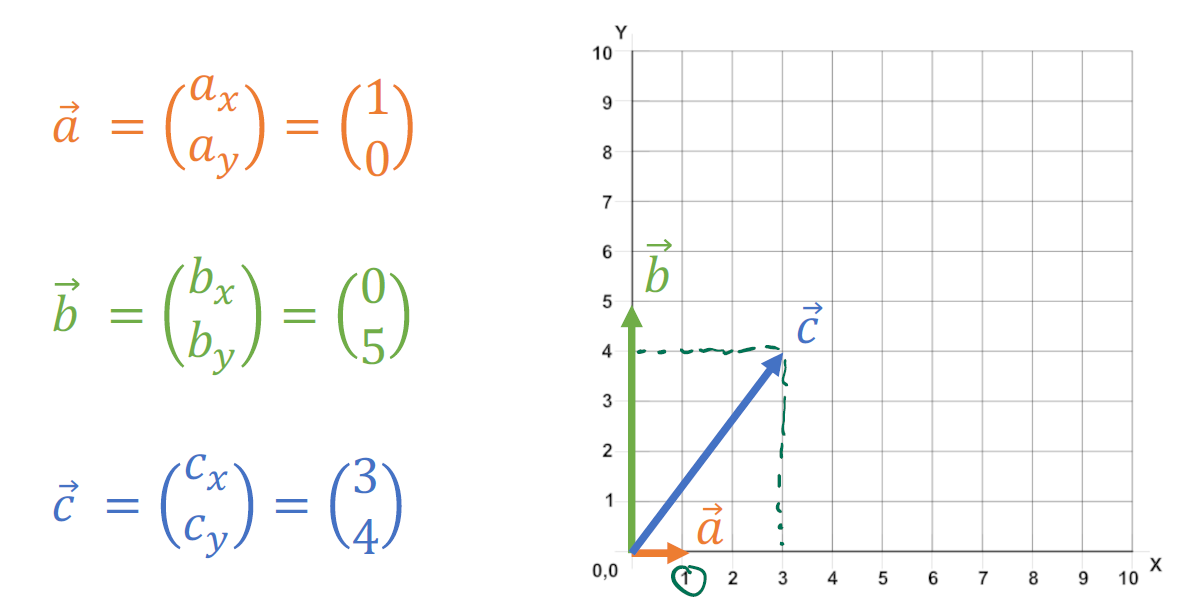
그리고 그래프는 위와 같이 X,Y 좌표계인 Cartesian Form 으로도 표현 가능하지만, 반경 r과 각도 Θ로 구성되는 Polar Form 으로도 표현 할 수 있다. 이때 반경 r 은 크기, 각도 Θ 은 방향을 의미한다

벡터의 크기

벡터의 크기는 Cartesian Form 으로는 선분의 거리를 의미한다. 예를 들어 V(3,4)인 벡터가 있다면 크기는 5가 된다

벡터의 방향

벡터의 방향은 Cartesian Form 일지라도 각도를 통해 표현한다. 그리고 이 각도를 위해선 앞서 배운 삼각법에서의 tan의 역함수인 arctan() 를 활용하면 된다.

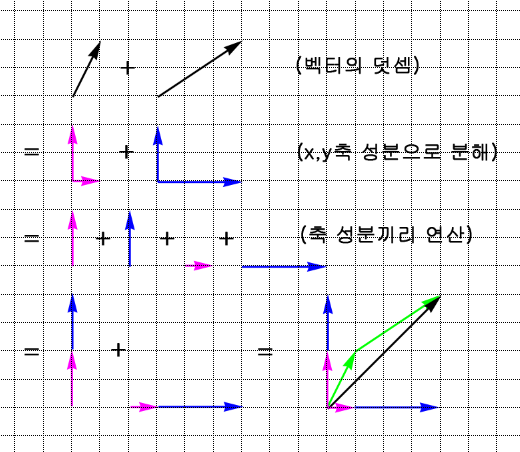
벡터 연산

벡터의 연산에서 더하기와 빼기는 기존의 사칙 연산 법과 같이 수행된다.
X 좌표는 X 좌표끼리, Y 좌표는 Y 좌표끼리 연산하면 된다. 또한, 단일 벡터의 크기는 곱셉을 통해 크기를 바꿀 수 있다.