최소 신장 트리 (MST, Minimal Spanning Tree), 크루스칼 알고리즘

shleecloud·2022년 2월 22일

Algorithm

목록 보기

11/16

들어가며

요즘 탐욕법을 중점적으로 공부하고 있다. 카테고리에서 탐욕법이라고 쓰여있으면 무작정 풀고 본다. 사실 이전에 알고리즘 공부를 열심히 한 적 있는데, 그 때 만났던 최소 신장 트리 문제를 다시 만났다. 이름만 보면 조금 어려워보인다. 막상 알고나면 간단하고 빠르고 좋다.

최소 신장 트리 (Minimal Spanning Tree)

신장 트리는 그래프에서 일부 간선만 선택해서 만든 트리.
최소 신장 트리는 간선 가중치(거리)의 합이 최소여야 한다.
트리이기 때문에 사이클(Loop)을 이루지 않는다.
모든 노드가 연결되어 있다.

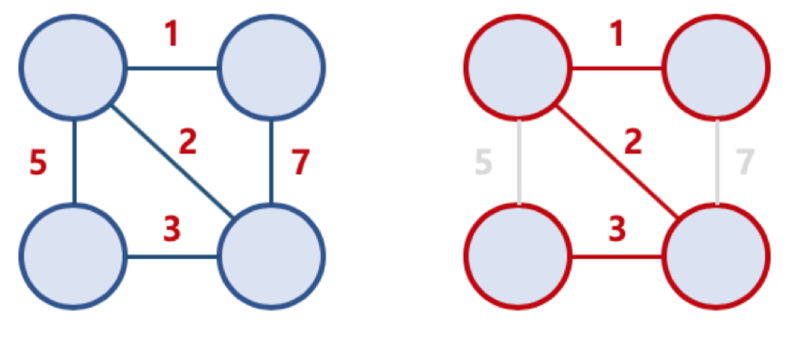
크루스칼 알고리즘

최소 비용으로 신장 트리를 찾는 알고리즘
탐욕법으로 동작
모든 간선을 가중치를 기준으로 오름차순 정렬
가장 가중치가 작은 간선부터 연결
매번 연결한 간선이 사이클을 이루는지 확인

Union-Find 알고리즘

새로 연결한 두 노드가 사이클을 이루는지 확인하는 기법
parent 배열을 만들어서 각 노드의 부모 노드를 관리
- 초기값은 자기 자신이 부모
- 새로 연결할 때 마다 부모 노드를 찾는 알고리즘 실행
- 자기 자신이 부모인 경우 그 노드가 최상위 부모
- 최상위 부모가 같은지 확인

최악의 경우 만난 노드만큼 부모를 찾게 되어 findParent 함수의 효율성이 떨어진다. 이를 보완하기 위해 Union-By-Rank 알고리즘으로 탐색 과정을 압축한다.

  function findParent(node) {
    if (parent[node] === node) return node;
    else return findParent(parent[node]);
  }

  function unionParent(left, right) {
    left = findParent(left);
    right = findParent(right);
    if (left === right) return false;
    parent[right] = left;
    return true;
  }

Union By Rank 알고리즘

Union-Find 알고리즘을 기반으로 한다.
rank 배열을 만들어서 부모 노드의 랭크를 관리한다.
- 노드를 추가할 때 랭크를 비교한다.
- 더 낮은 랭크의 부모는 더 높은 랭크의 부모로 대체된다.
- 랭크가 같을 경우 노드 한 쪽의 랭크를 높이고 부모로 만든다.

function solution(n, costs) {
  // * union-find 구현
  let result = 0;
  const parent = Array(n)
    .fill(0)
    .map((el, idx) => idx);
  // * union by rank
  const rank = Array(n).fill(0);

  function findParent(node) {
    if (parent[node] === node) return node;
    else return findParent(parent[node]);
  }

  function unionParent(left, right) {
    left = findParent(left);
    right = findParent(right);
    if (left === right) return false;
    if (rank[left] < rank[right]) parent[left] = right;
    else {
      parent[right] = left;
      if (rank[left] === rank[right]) rank[left]++;
    }
    return true;
  }

시간 복잡도 O(E log E)

크루스컬 알고리즘의 시간 복잡도는 간선의 숫자에 비례함.
간선을 정렬하는데 시간 복잡도가 가장 많이 소요된다. 퀵정렬의 시간복잡도는 O(N log N) 이므로 간선에 대입되니 O(E log E)
사이클이 존재하는지 확인하는 과정은 Union-Find, Union-By-Rank 기법으로 인하여 상수에 가까워짐

섬 연결하기 (크루스칼 알고리즘)

https://programmers.co.kr/learn/courses/30/lessons/42861

function solution(n, costs) {
  // * union-find 구현
  let result = 0;
  const parent = Array(n)
    .fill(0)
    .map((el, idx) => idx);
  // * union by rank
  const rank = Array(n).fill(0);

  function findParent(node) {
    if (parent[node] === node) return node;
    else return findParent(parent[node]);
  }

  function unionParent(left, right) {
    left = findParent(left);
    right = findParent(right);
    if (left === right) return false;
    if (rank[left] < rank[right]) parent[left] = right;
    else {
      parent[right] = left;
      if (rank[left] === rank[right]) rank[left]++;
    }
    return true;
  }

  // * cost 순서로 내림차순 정렬
  const sortedCosts = costs.slice().sort((a, b) => b[2] - a[2]);
  for (let i = 0; i < costs.length; i++) {
    let [from, to, cost] = sortedCosts.pop();
    if (unionParent(from, to)) result += cost;
  }
  return result;
}

console.log(
  solution(5, [
    [0, 1, 1],
    [3, 4, 1],
    [1, 2, 2],
    [2, 3, 4],
  ])
);

// n / costs / answer
// 5 [[0, 1, 5], [1, 2, 3], [2, 3, 3], [3, 1, 2], [3, 0, 4], [2, 4, 6], [4, 0, 7]] 15
// 5 [[0, 1, 1], [3, 4, 1], [1, 2, 2], [2, 3, 4]] 8
// 4 [[0, 1, 5], [1, 2, 3], [2, 3, 3], [1, 3, 2], [0, 3, 4]] 9
// 5 [[0, 1, 1], [3, 1, 1], [0, 2, 2], [0, 3, 2], [0, 4, 100]] 104
// 6 [[0, 1, 5], [0, 3, 2], [0, 4, 3], [1, 4, 1], [3, 4, 10], [1, 2, 2], [2, 5, 3], [4, 5, 4]] 11
// 5 [[0, 1, 1], [2, 3, 1], [3, 4, 2], [1, 2, 2], [0, 4, 100]] 6
// 5 [[0, 1, 1], [0, 4, 5], [2, 4, 1], [2, 3, 1], [3, 4, 1]] 8
// 5 [[0, 1, 1], [0, 2, 2], [0, 3, 3], [0, 4, 4], [1, 3, 1]] 8