데이터 분석 Study-02

대푯값
1. 평균. 유일한 값을 가짐. 극단값에 민감해서 극단값이 여러 개인 경우 대푯값의 기능을 상실한다.

위치 통계량(중심 경향성)
중앙값(median):데이터를 순서대로 나열할 때 가운데 있는 값
최빈값(mode):가장 많이 나온 값. 여러 개 있을 수 있다. 질적 변수에도 활용 가능
변이 통계량(퍼짐의 정도)
산포도 혹은 분산도(measure of dispersion)는 자료가 흩어져 있는 정도를 측정한다. 두 분포에서 자료의 흩어짐을 비교하는데 이용한다.

• 범위: 최대값, 최소값의 차이값
• 중간범위: 최대값과 최소값의 평균
• 평균절대편차: 모든 데이터로부터 평균값을 뺀 값의 절대값의 평균
• 분산, 표준편차, 변동계수 등이 있다.
  데이터의 불규칙성, 변동성, 데이터의 특수성을 알고 싶을 때 분산과 표준편차를 이용한다.

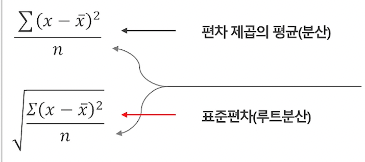
sample에 대해서는 n 대신 n-1로 나눈다.

분산은 원자료의 단위와 달라진다.
표준편차는 분산에 루트를 씌운 것.

• 변동 계수(변이 계수) : coefficient of variation/ relative standard deviation. 표준편차를 평균으로 나눈 값. 서로 다른 데이터 간의 편차를 비교하는 방법.

오른쪽 꼬리가 긴 왜도: positive. 양의 왜도
왼쪽 꼬리가 긴 왜도: negative. 음의 왜도

확률

• 0에서 1사이의 값을 가지고,
• 모든 사건에 대한 확률의 합은 1이다.
• 배반사상인 경우 ->겹치는 부분이 없다. 𝗣₍𝐀∪𝑩₎⁼𝐏₍𝐀₎₊𝐏₍𝐁₎
• 배반사상의 관계에서 곱사건의 경우 𝐏₍𝐀∩𝐁₎₌𝐏₍𝐀₎𝐏₍𝐁₎

일반적인 형태의 곱셈 법칙

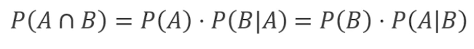
독립인 경우의 곱셈 법칙

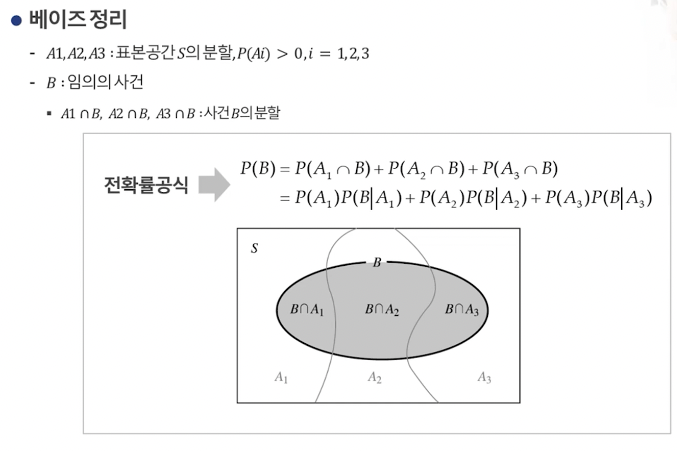
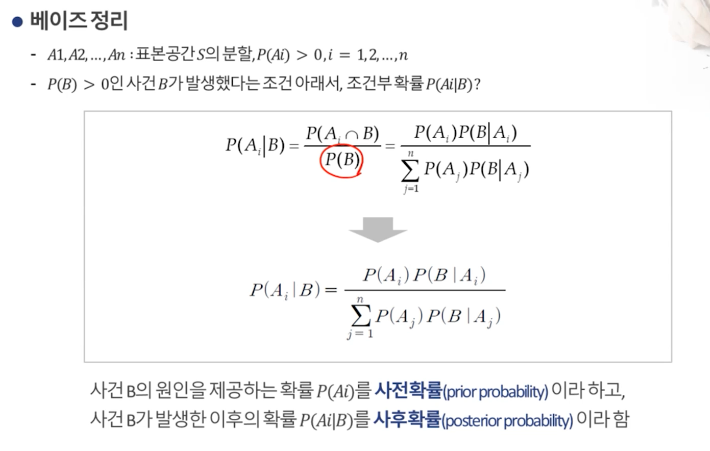
베이즈 정리(=사후확률)