K-D Tree

Binary Search Tree

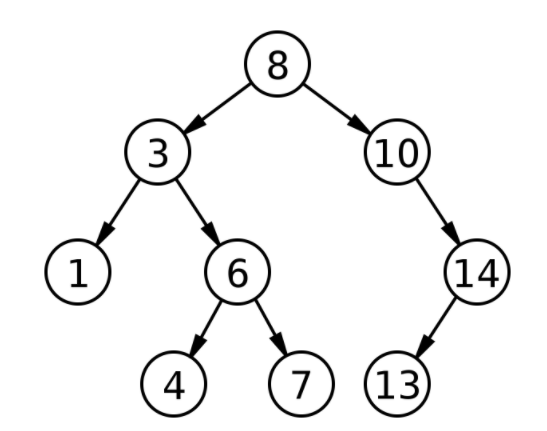
• A binary search tree is a tree in which the left side has a small value and the right side has a large value based on a specific node.
• The depth of the tree is log(n), so the search ends in O(log(n)) time in Big O notation.

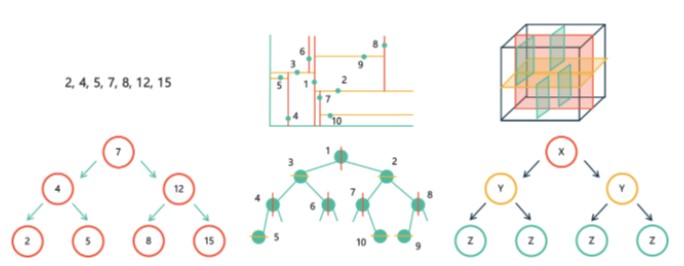
K-D tree

• KD-Tree is a concept that extends Binary Search Tree, and uses a key consisting of k (k>=2) fields for operation.
• Ideal for indexing small, multidimensional point data.

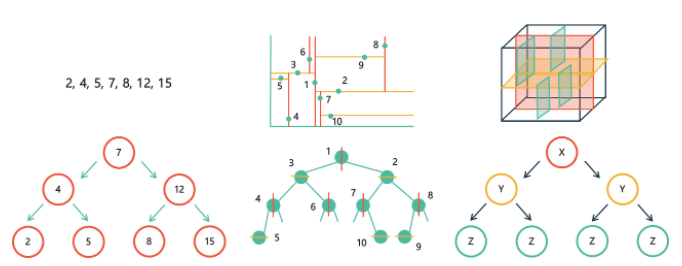
Algorithm

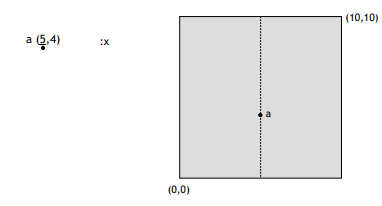
1. insert (a) as root

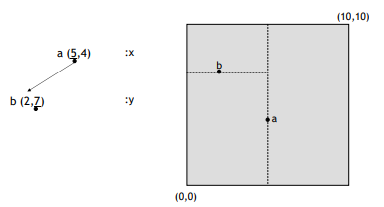
2. compare (b) x axis to (a) x axis and insert left side of left branch

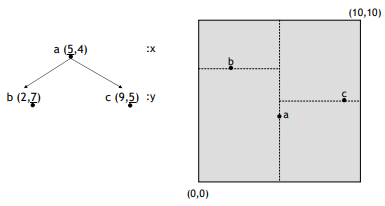
3. compare (c) x axis to (a) x axis and insert right side of left branch

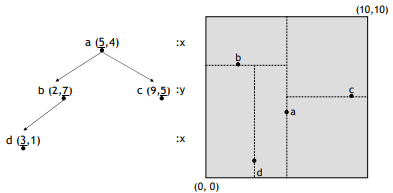
4. compare (d) x axis to (a) axis and then compare (d) y axis to (b) insert left side of left branch

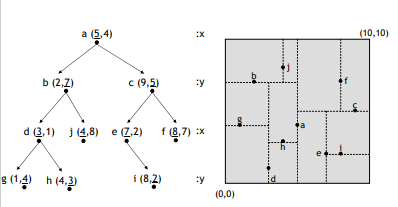
Limitation

• Not a balanced tree
• Can be skewed according to data entry order and distribution

Insert Operation

• Basically, it is the same as insertion operation in Binary Search Tree.
• When a leaf node is encountered while going down the tree, it decides whether to insert into the left child or the right child based on the key value.

Deletion Operation

• In KD-Tree, one node can have up to two children, and the deletion method according to the number of children is as follows.
  • # of Child = 0 - Just remove the target node to be removed.
    (There is no child, so there is nothing to worry about.)
  • # of Child = 2 - Among the nodes in the right subtree of the node to be removed,
    Remove the node with the smallest Field value used by the node to be removed and put it in the position of the node to be removed.
    - If the newly located node has a child, it recursively finds a replacement node for this node.
  • # of Child = 1- If there is only the right child, from among the nodes in the right subtree, the node with the smallest field value of the node to be removed is removed and placed in the position of the node to be removed.
    - If there is only a left child, from among the nodes in the left subtree, the node with the largest field value of the node to be removed is removed and placed in the position of the node to be removed.

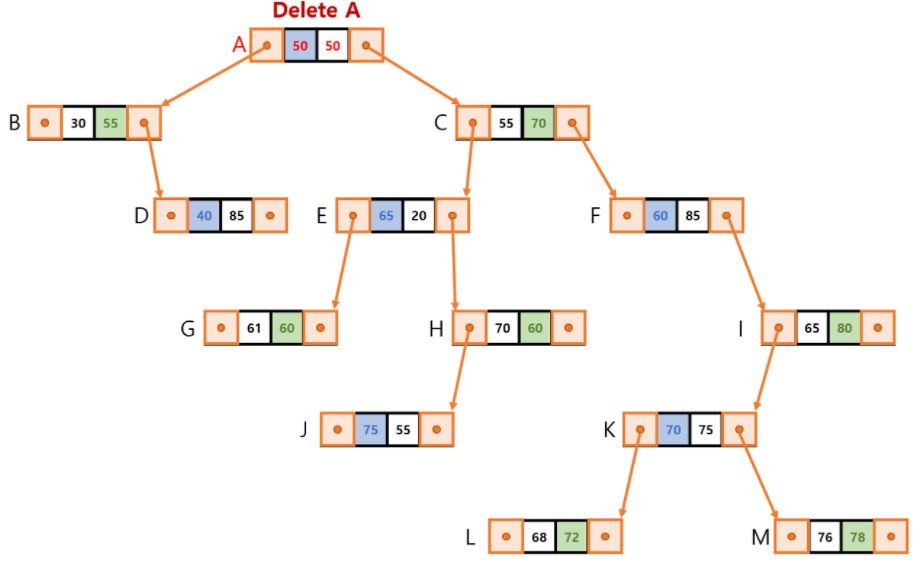
1) Delete Node A

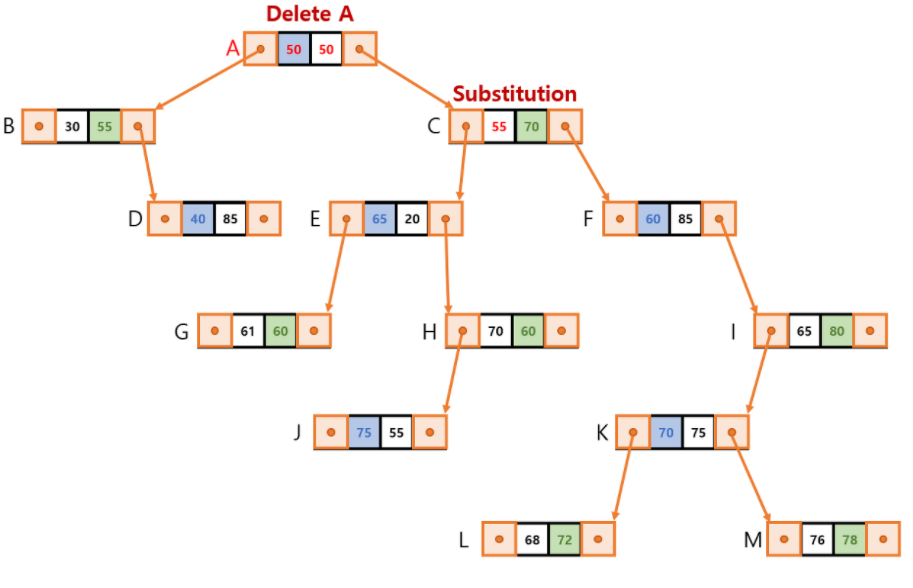
2. Detect Substitution

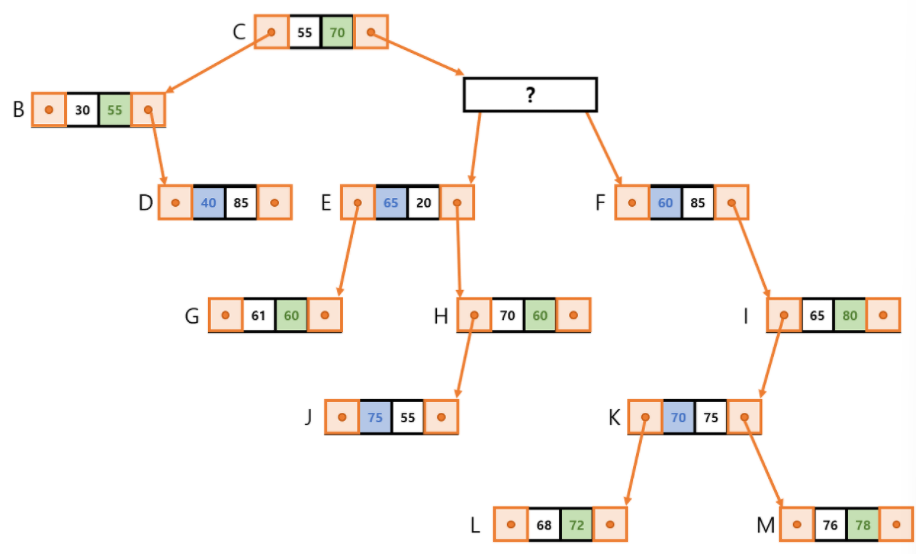
3. Remove A & Relocating C

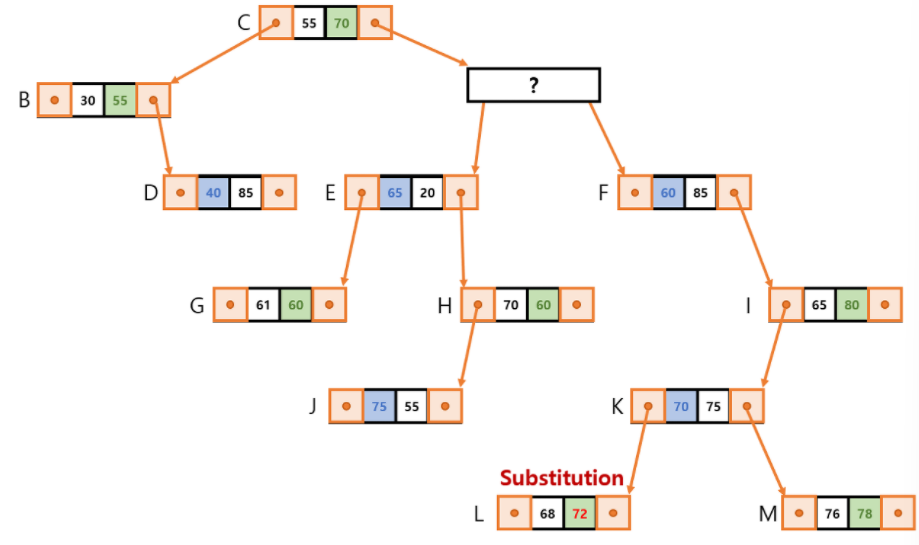
4. Remove C

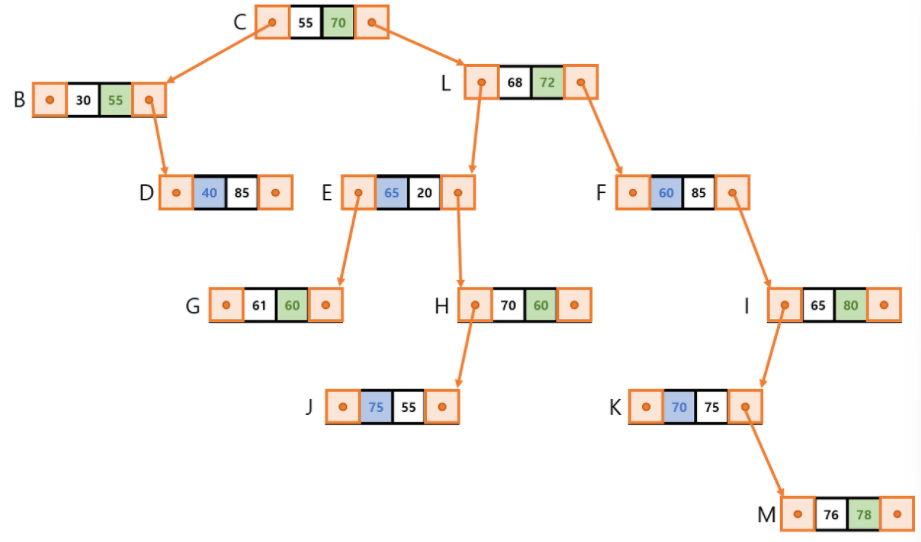
5. Relocating L

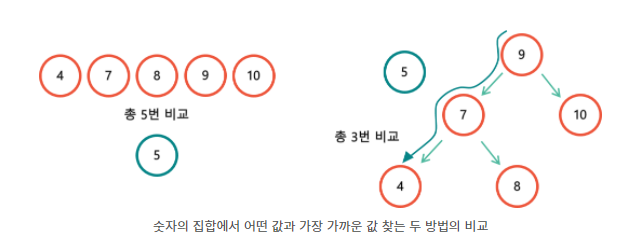
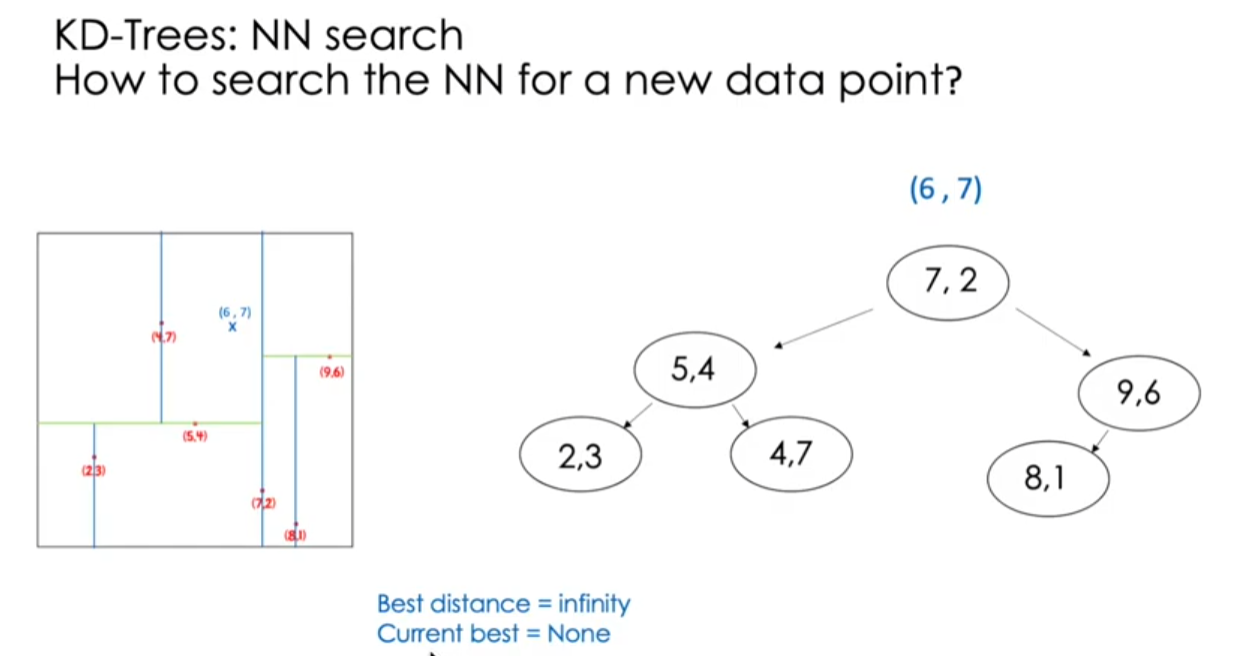
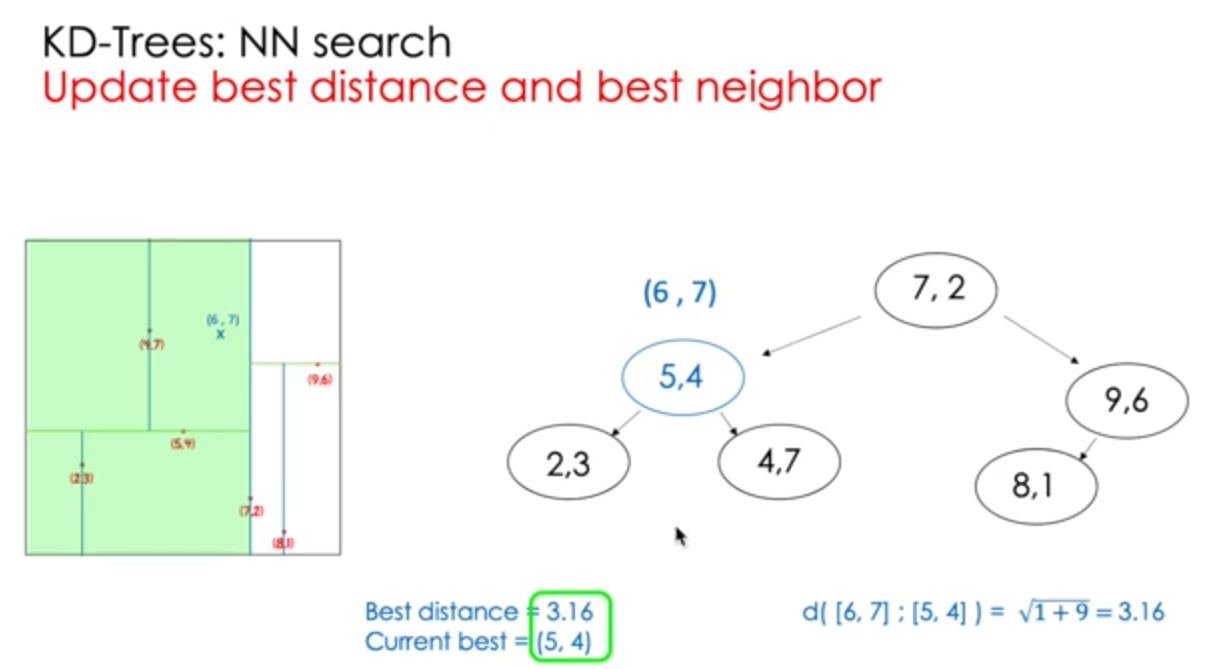
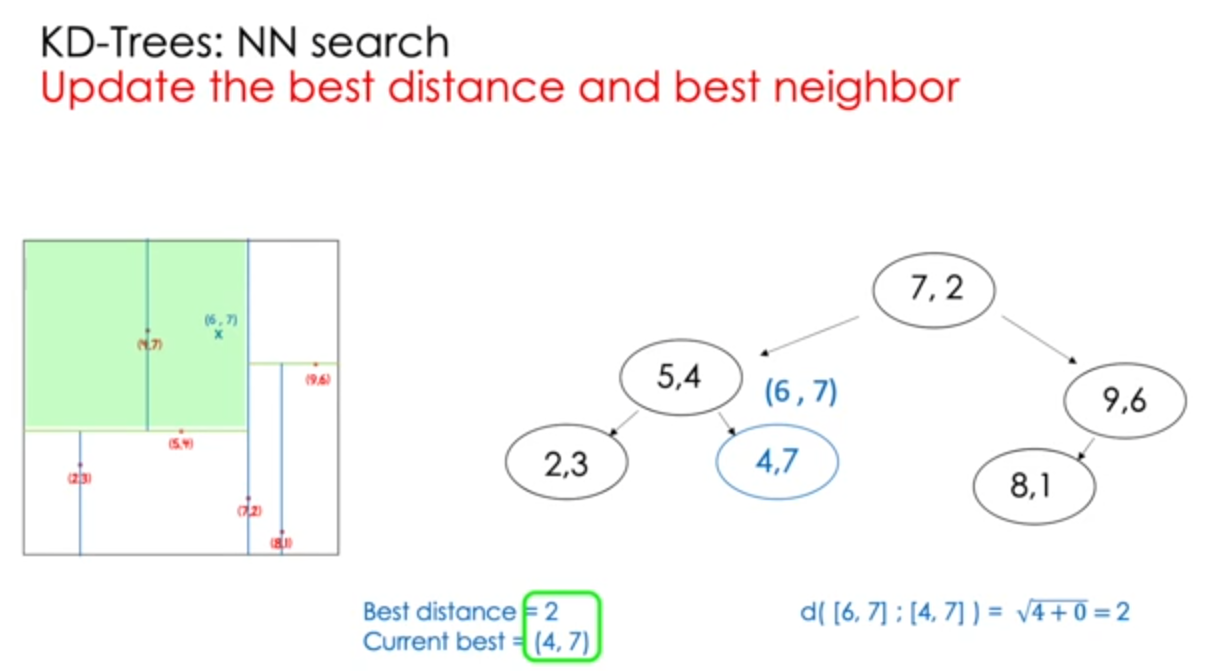
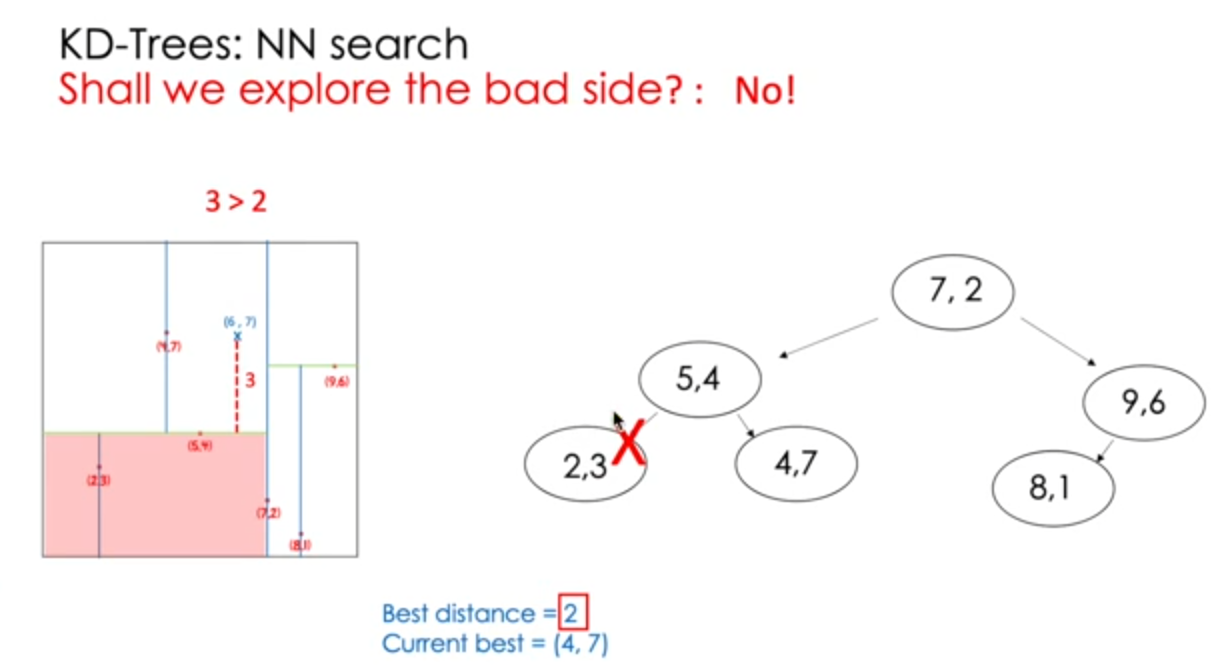
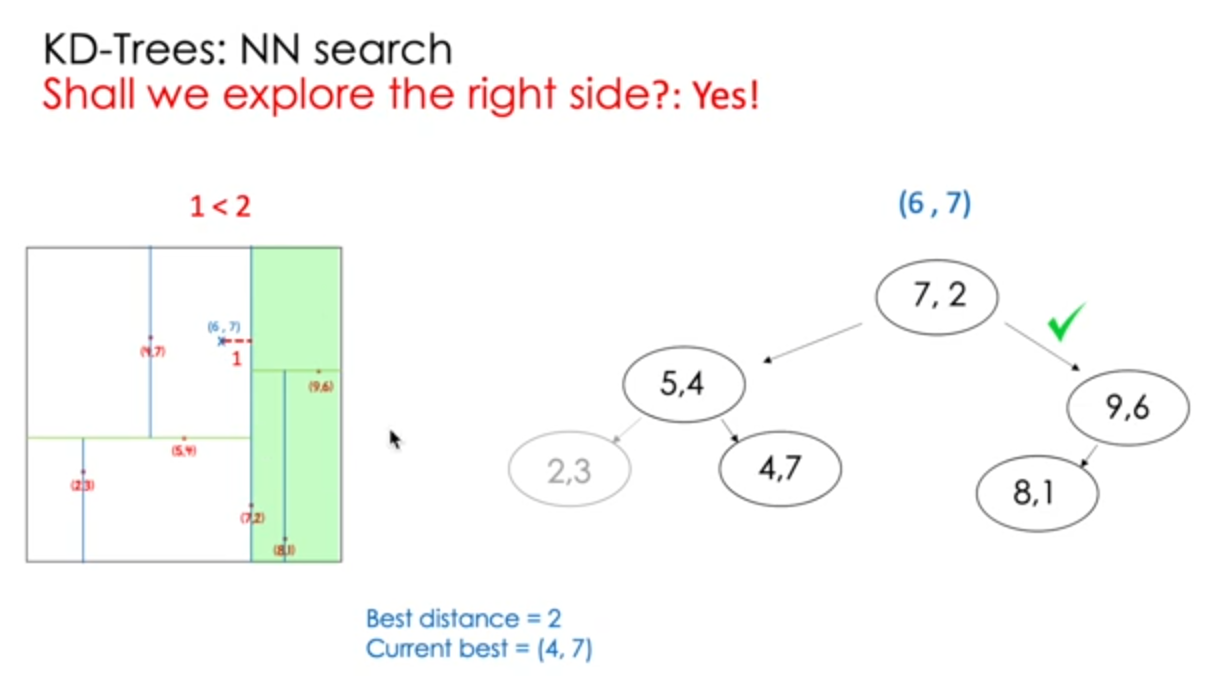
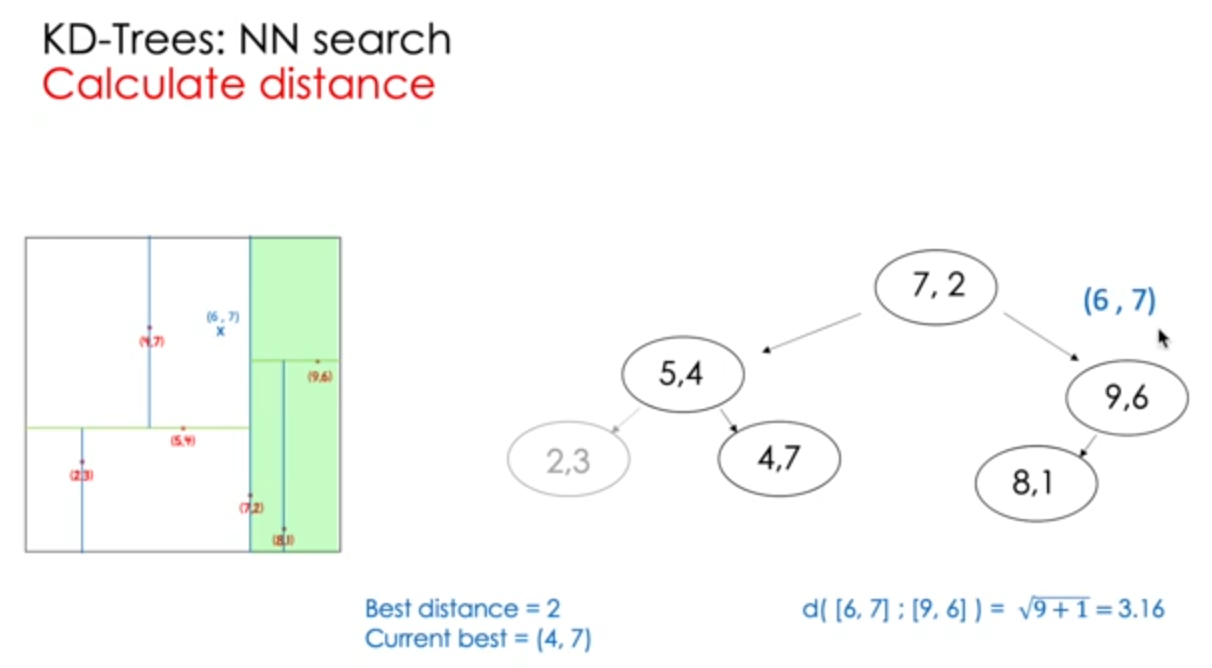
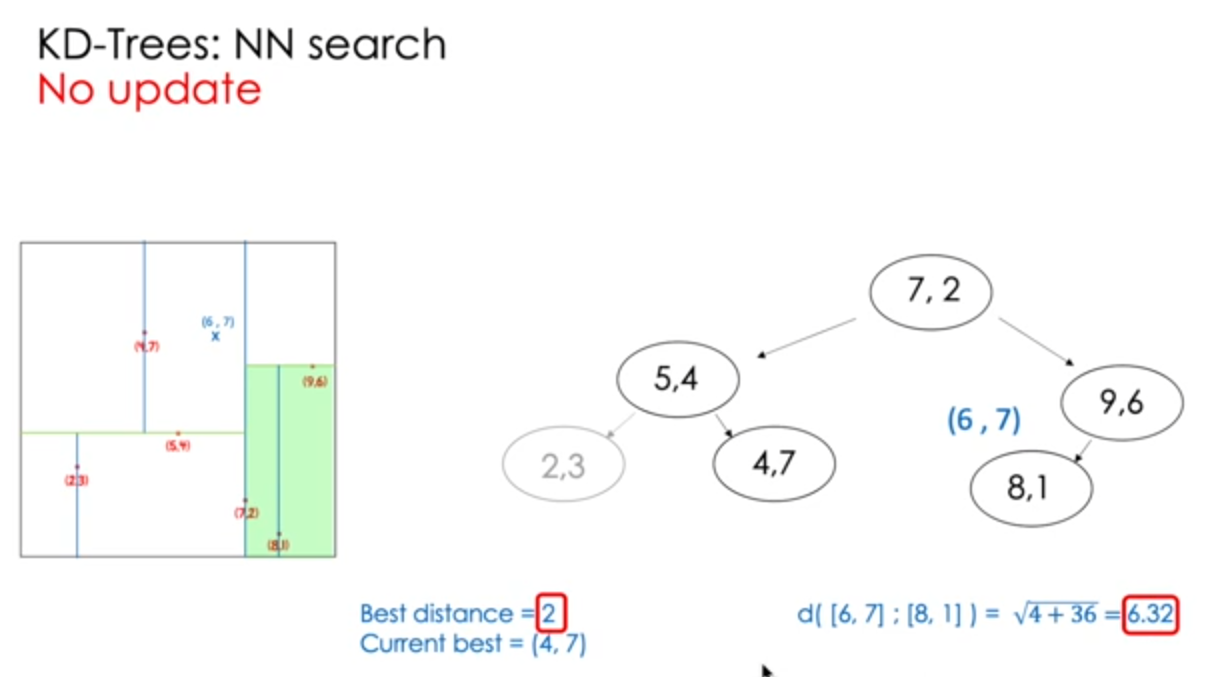
NN search

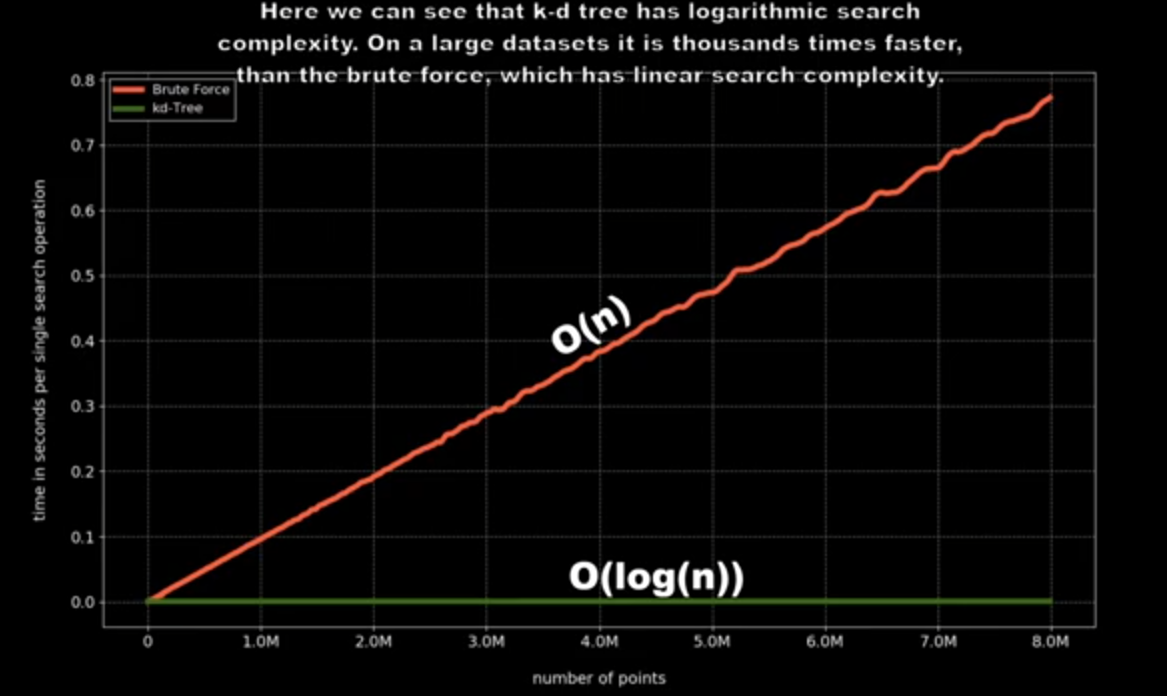
Performance Evaluation