[Lv.2 / Programmers / Java] 땅따먹기

땅따먹기

문제 설명

땅따먹기 게임을 하려고 합니다. 땅따먹기 게임의 땅(land)은 총 N행 4열로 이루어져 있고, 모든 칸에는 점수가 쓰여 있습니다. 1행부터 땅을 밟으며 한 행씩 내려올 때, 각 행의 4칸 중 한 칸만 밟으면서 내려와야 합니다. 단, 땅따먹기 게임에는 한 행씩 내려올 때, 같은 열을 연속해서 밟을 수 없는 특수 규칙이 있습니다.

예를 들면,

| 1 | 2 | 3 | 5 |

| 5 | 6 | 7 | 8 |

| 4 | 3 | 2 | 1 |

로 땅이 주어졌다면, 1행에서 네번째 칸 (5)를 밟았으면, 2행의 네번째 칸 (8)은 밟을 수 없습니다.

마지막 행까지 모두 내려왔을 때, 얻을 수 있는 점수의 최대값을 return하는 solution 함수를 완성해 주세요. 위 예의 경우, 1행의 네번째 칸 (5), 2행의 세번째 칸 (7), 3행의 첫번째 칸 (4) 땅을 밟아 16점이 최고점이 되므로 16을 return 하면 됩니다.

제한사항

• 행의 개수 N : 100,000 이하의 자연수
• 열의 개수는 4개이고, 땅(land)은 2차원 배열로 주어집니다.
• 점수 : 100 이하의 자연수

예시

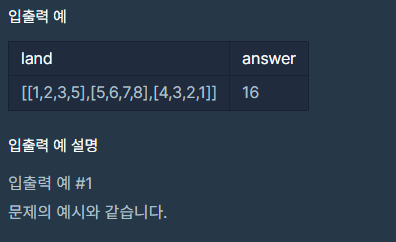
풀이

각 행에서 4개의 선택지 중 하나를 선택할 수 있고 같은 열을 연속으로 선택할 수 없기 때문에 모든 경우의 수는 O(3^N)에 가깝기 때문에 완전탐색으로는 시간복잡도가 안된다.

그래서 이 문제는 DP를 통해 각 칸의 누적 최대 점수를 계산함으로써 해결했다.
land[i][j]는 i행 j열까지 왔을 때 얻을 수 있는 최대 점수로 갱신되고 이전 행에서 같은 열을 제외한 열 중 최대값을 더하는 방식으로 구현했다.

예를 들어 [[1,2,3,5], [5,6,7,8], [4,3,2,1]]로 진행 시 첫 번째 행은 그대로 유지하고

두 번째 행부터 이전 행을 참조해 누적합을 계산한다.

land[1][0] = 5 + max(2, 3, 5) = 10
land[1][1] = 6 + max(1, 3, 5) = 11
land[1][2] = 7 + max(1, 2, 5) = 12
land[1][3] = 8 + max(1, 2, 3) = 11

→ 두 번째 행은 [10, 11, 12, 11]

land[2][0] = 4 + max(11,12,11) = 16
land[2][1] = 3 + max(10,12,11) = 15
land[2][2] = 2 + max(10,11,11) = 13
land[2][3] = 1 + max(10,11,12) = 13

→ 세 번째 행은 [16, 15, 13, 13]

이렇게 다 구한 후 마지막 행에서 최댓값을 리턴해주면 된다.

import java.util.*;

class Solution {
    int solution(int[][] land) {
        int answer = 0;

        for(int i=1; i<land.length; i++) {
            land[i][0] += Math.max(Math.max(land[i - 1][1], land[i - 1][2]), land[i - 1][3]);
            land[i][1] += Math.max(Math.max(land[i - 1][0], land[i - 1][2]), land[i - 1][3]);
            land[i][2] += Math.max(Math.max(land[i - 1][0], land[i - 1][1]), land[i - 1][3]);
            land[i][3] += Math.max(Math.max(land[i - 1][0], land[i - 1][1]), land[i - 1][2]);
        }
        
        answer = Arrays.stream(land[land.length - 1]).max().getAsInt();

        return answer;
    }
}