reference :
https://github.com/taehojo/deeplearning
목차
1) Ch04 가장 훌륭한 예측선
2) 선형 회귀 모델 : 먼저 긋고 수정하기
3) 로지스틱 회귀 모델 : 참 거짓 판단하기
4장 가장 훌륭한 예측선
딥러닝은 자그마한 통계의 결과들이 얽힌 통계의 결정체다.
딥러닝을 이해하기 위해서는 가장 말단의 두가지 계산 원리를 알아야한다.
바로 선형회귀와 로지스틱 회귀다.
4장에서는 선형회귀(linear regression)분석에 대해서 다룬다.
1) 선형회귀의 정의
어떤 x라는 변수가 있을 때, 이 변수 x에 따라 y라는 결과가 바낀다고 할 떄
이 변수 x를 독립변수, 변수 x에 따라 값이 바끼는 y를 종속변수라고 한다.
만약 하나의 x값으로 y에 대해 설명할 수 있다면 단순 선형회귀(simple linear regression)
여러 x(x2,...xn)등이 필요하다면 다중 선형 회귀(multiple linear regression)
이라고 한다.
2) 가장 훌륭한 예측선이란?
단순 선형회귀 예시
공부한 시간 -> 성적일 때
공부한 시간
2시간 -> 81점
4시간 -> 93점
6시간 -> 91점
8시간 -> 97점
X = {2,4,6,8}
Y = {81,93,91,97}
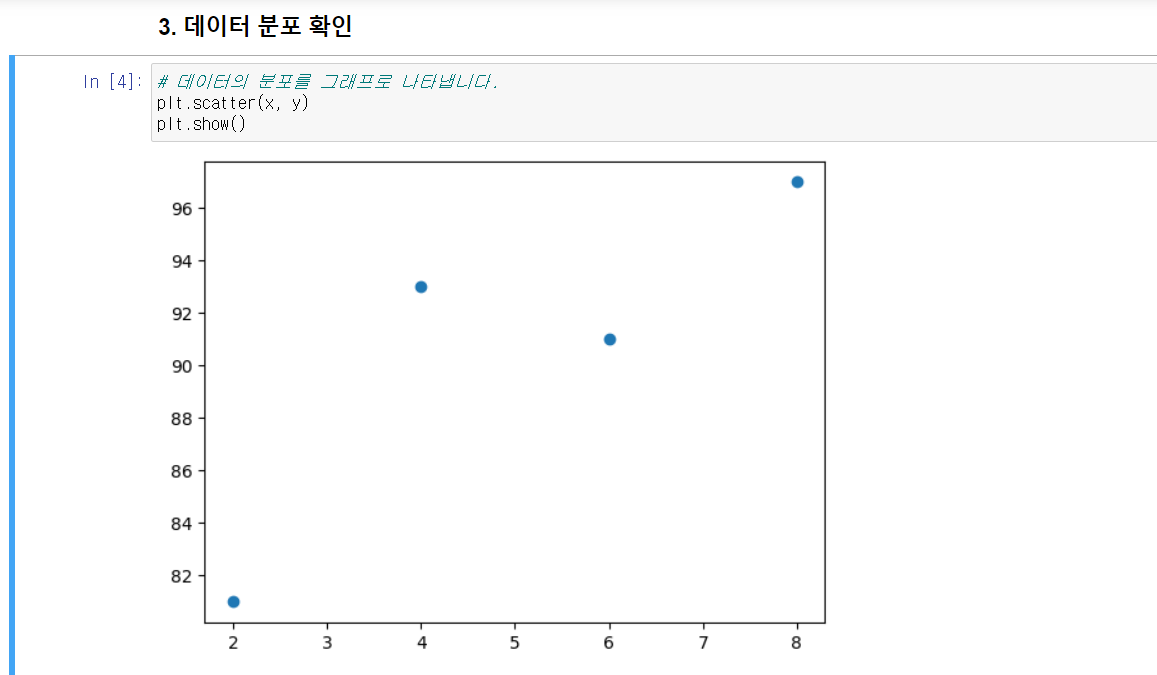
이를 좌표평면에 나타내면 선형과 유사한 것을 볼 수 있다. (엑셀 참조)
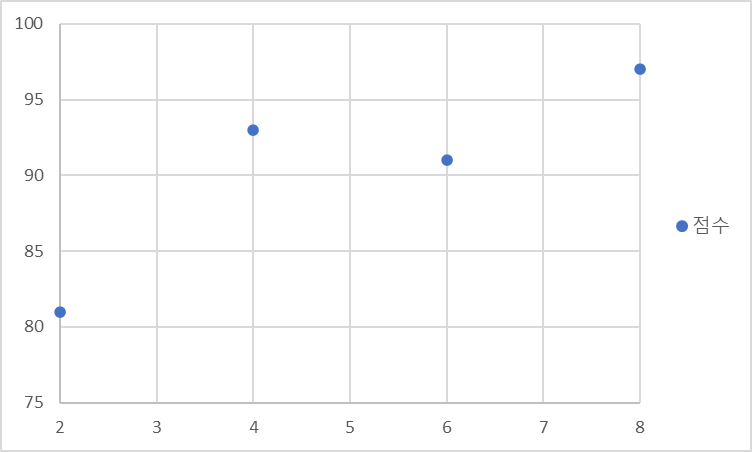
이러한 일차함수의 그래프는 y = ax + b의 형태로 나타낼 수 있다.
3) 최소제곱법
좌표평면 위에 점을 나타냈으니 이제 선을 긋는 방법 즉 정확한 기울기 a와
정확한 y절편 b를 알아내야 한다. 이 때 쓰는 방법이 바로 최소제곱법(method of least squares)다.
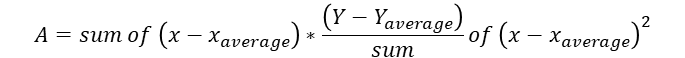
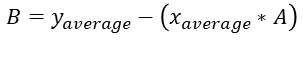
이다.
위의 공식들을 대입하면
y=2.3x+79라는 것을 알 수 있다.
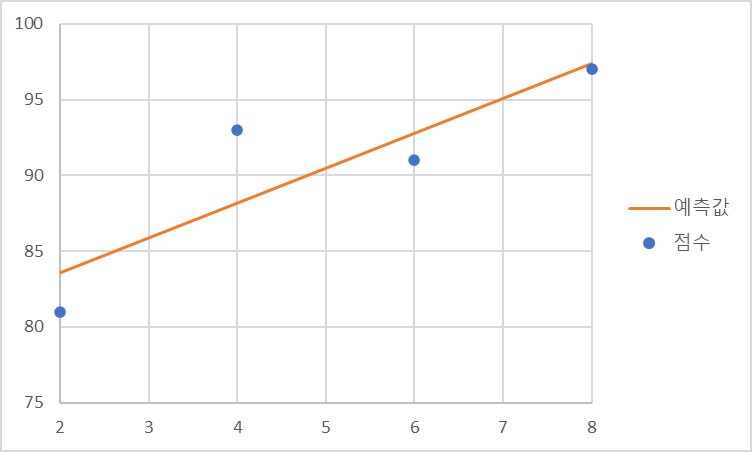
4) 파이썬 코딩으로 확인하는 최소제곱
다음은 엑셀을 이용하여 했던 최소제곱법의 구현을 파이썬을 이용해서 나타내 보겠다.


5) 평균제곱오차
최소제곱법을 이용해 기울기 a와 y절편을 구했지만, 다른 방법이 필요하다.
선을 긋고나서 수정하기 방식이다. 이를 위해 주어진 선의 오차를 평가하는 방법이 필요하다.
이 방법이 평균제곱오차(Mean Square Error, MSE)다.
이와 같이 임의의 직선을 구했을 때 두 점 사이의 거리 즉 오차가 작아야만 한다.
오차는 실제값 -예측값이다.
평균제곱오차 공식은 다음과 같다.

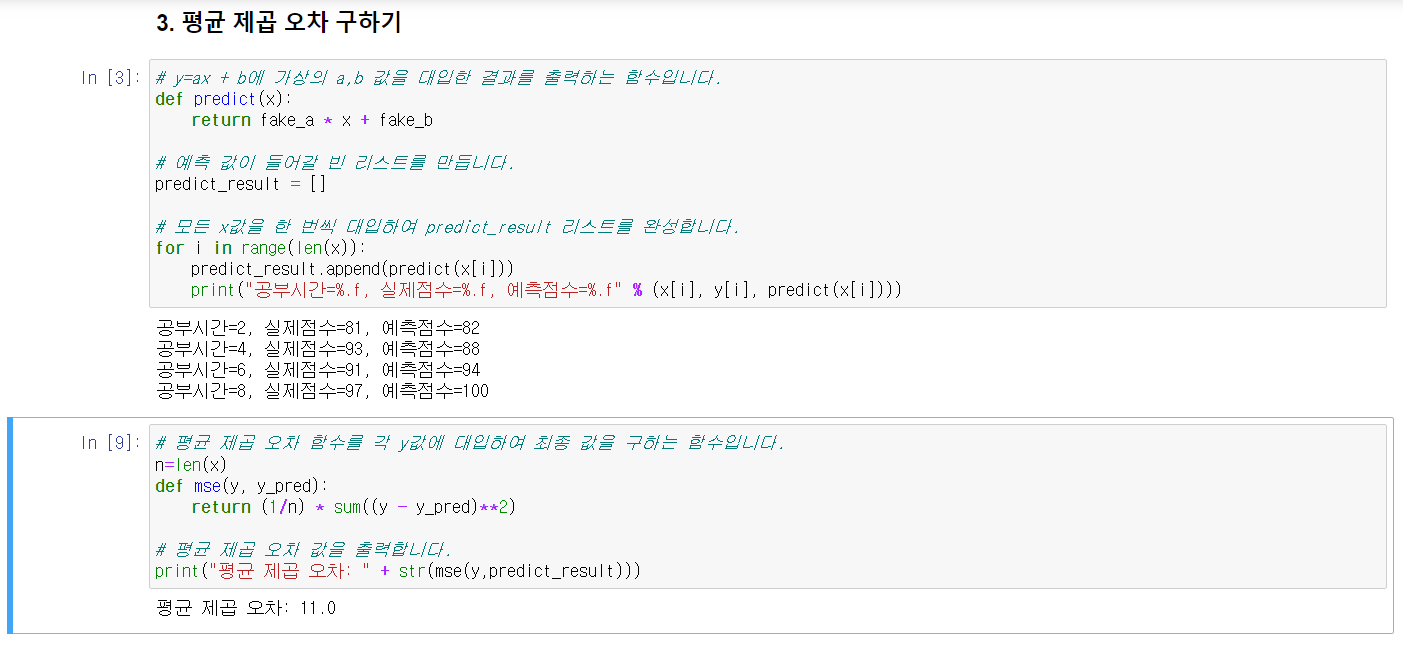
이렇듯 MSE는 11이라는 것을 알 수 있다.
6) 다음은 파이썬 코딩으로 평균제곱오차를 구하는 방법이다.
5장 선형 회귀 모델: 먼저 긋고 수정하기
기울기 a를 너무 크게 잡으면 오차가 커진다는 것을 확인하였다.
이때 오차가 제일 작은 최솟값을 잡아야 하는데 그것을 하는 방법은
위의 그래프에서 x는 0(미분 기울기는 0인 곳)에 이르면 최솟값을 가진다는 것을 알 수 있다.
이렇게 미분 기울기를 이용해 경사를 낮추며 찾는 방법을 경사하강법(gradient decent)라고 한다.

1) 경사 하강법의 개요
위의 2차함수를 보면 최솟값의 기울기가 0이라는 것을 확인할 수 있다.
미분 값이 0인 지점을 찾기 위해서는 이러한 방법을 써야한다.
1) 임의의 점 a1에서 미분을 구한다.
2) 구한 기울기의 반대 방향으로 얼마 이동시킨 a2에서 미분을 구한다.
3) 0이 아니면 1과 2과정을 반복한다.
이때 너무 크게 이동시키면 값이 위로 치솟아 버리게 된다. 이때 학습률이라는 개념이 중요한데
적절한 학습률을 넣어서 미분값이 0인 지점을 구해야 한다.
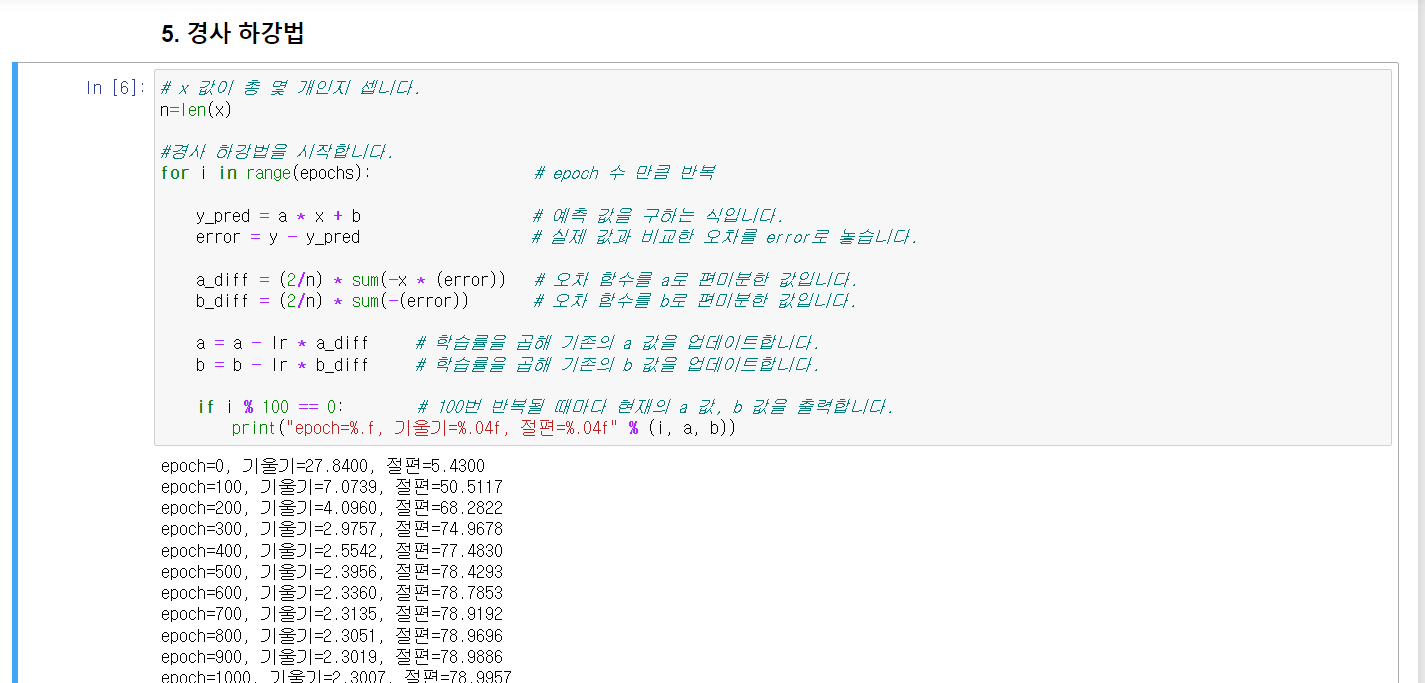
2) 파이썬 코딩으로 확인하는 선형회귀
앞의 평균 제곱 오차의 식을 ax_i+b를 대신 대입해서 넣으면 a와 b의 변수로 바뀌는데
이 식을 a와 b라는 변수로 편미분을 할 수 있다.
나머지는 동일하다.



3) 다중 선형 회귀의 개요
앞에서는 하나의 변수만 다뤘지만 이번에는 결과에 영향을 주는 다른 요소들을 추가해서 오차를 줄여보는 방법인 다중 선형회귀에 대해 다룰 것이다.
이를 그래프로 나타내면 다음과 같다.
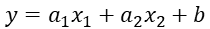
4)파이썬 코딩으로 확인하는 다중 선형 회귀
1) 변수 설정 및 데이터 제시
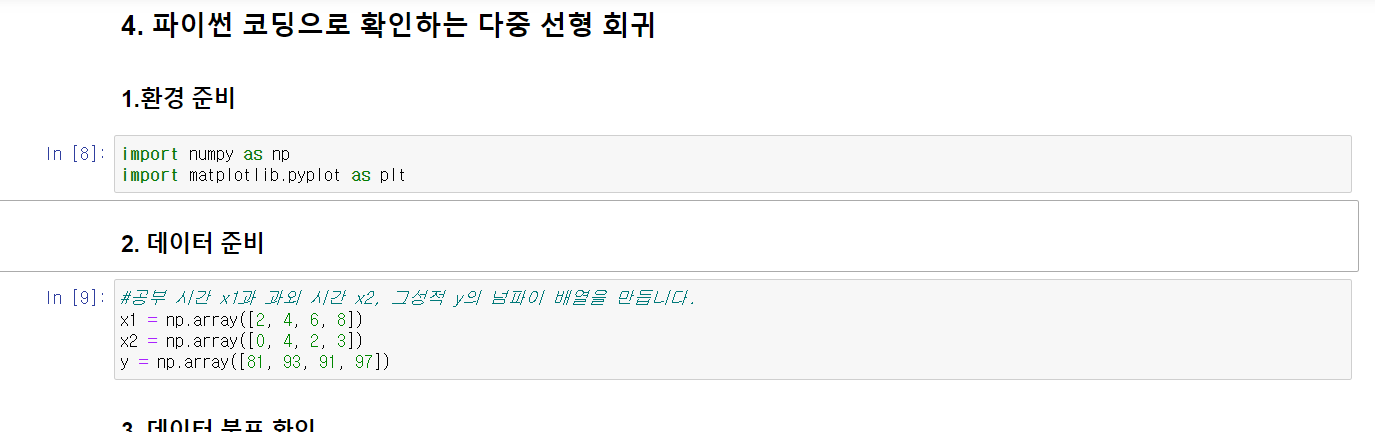
데이터 분포 확인(3d로)
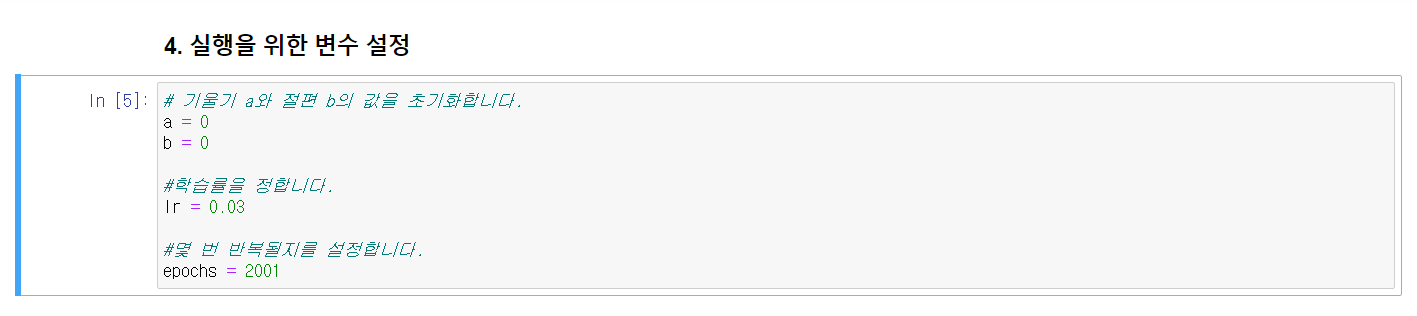
실행을 위한 변수 설정 (epoch =2001->2001번 반복한다.)
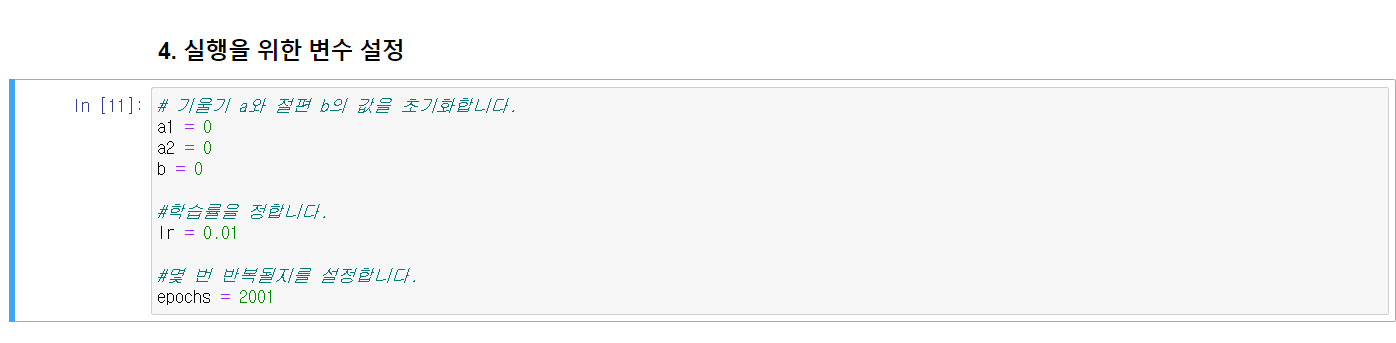
경사하강법 알고리듬
실제점수 & 예측점수 출력

5) 텐서플로에서 실행하는 선형 회귀, 다중 선형 회귀 모델
2장에서 잠시 keras와 tensorflow를 다뤄봤듯이 이 사용법을 익힐 것이다.
선형회귀는 현상을 분석하는 하나의 방법이다. 머신 러닝은 이러한 분석 방법을 이용해 예측 모델을 만드는 것이다.
y = ax+b처럼 유추하는 식을 가설 함수(hypothesis)라고 하고 H(x)라고 표기한다. 또 기울기 a는 변수 x에 어느 정도의 가중치를 곱하는지 결정하는 가중치(weight)라고 하며 w로 표시한다.
또한 평균제곱오차 같은 오차에 대한 식을 손실 함수(loss function)이라고 한다.
경사하강법 같이 최적의 기울기와 절편을 찾는 방법을 딥러닝에서는 옵티마이저라고 한다.
코드를 실행하였을 때 입력된 값을 어떻게 처리할지를 결정하는 함수를 활성화 함수라고 한다.
이런 방식으로 다중 선형 회귀 모델을 통해 예상점수를 확인할 수 있었다.
6장 로지스틱 회귀 모델: 참 거짓 판단하기
딥러닝에서 참, 거짓을 내놓는 과정은 로지스틱 회귀(logistic regression)의 원리를 거쳐 이루어진다.
이번 챕터에선 로지스틱 회귀에 대해서 다뤄보겠다.
1) 로지스틱 회귀의 정의
5장에서 공부한 것처럼 좌표의 형태가 직선으로 해결되지 않고 합격과 불합격만 내놓는 결과가 있을 때
예)
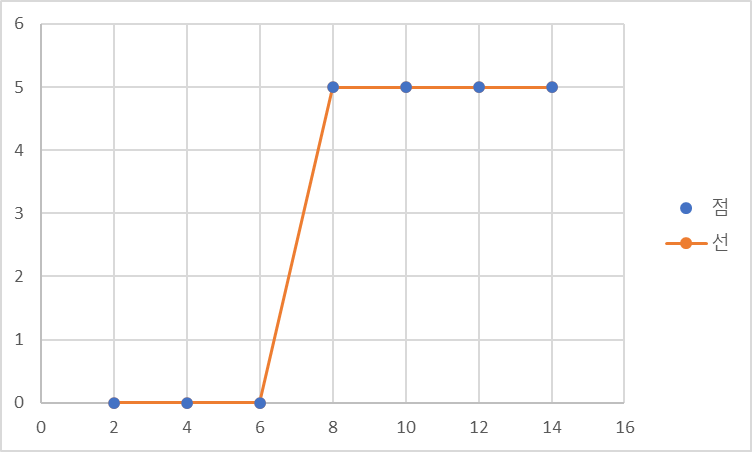
이러한 형태로 그려진다.
이 점들은 1과 0사이의 값이 없으므로 참(1)과 거짓(0)을 구분하기 어려워진다.
2) 시그모이드 함수
이러한 시그모이드 함수를 통해 참과 거짓을 알 수 있다. 여기서 a는 경사도를 b는 좌우 이동을 나타낸다.
따라서 a값 b의 값이 오차를 만든다. a값이 작아지면 오차는 무한대로 커진다. a값이 커진다고 해서 오차가 0이 되지는 않는다. b의 경우는 b가 너무 크거나 작을 경우 오차는 이차함수의 그래프와 유사한 형태를 띈다.
3) 오차공식
a값과 b값을 구하려면 앞과 동일하게 경사하강법을 써야한다. 하지만 평균제곱오차는 쓰지 않는다. 실제값이 1일 때 예측값이 0에 가까워지면 오차가 커진다. 반대도 마찬가지기에 로그 함수가 필요하다.
4) 로그 함수
5)텐서플로에서 실행하는 로지스틱 회귀 모델
위의 함수들을 실행하면 학습된 모델의 테스트를 위해 여러 가지 임의의 시간을 집어넣고 테스트 해보면,
학습 시간이 7보다 클 경우 합격률이 50%가 넘는다는 것을 알 수 있다.
다음에는 로지스틱 회귀모델의 전신인 퍼셉트론과 퍼셉트론의 한계를 극복하며 탄생한 신경망에 대해 알아보겠다.
