백준 10942, 팰린드롬? - DP

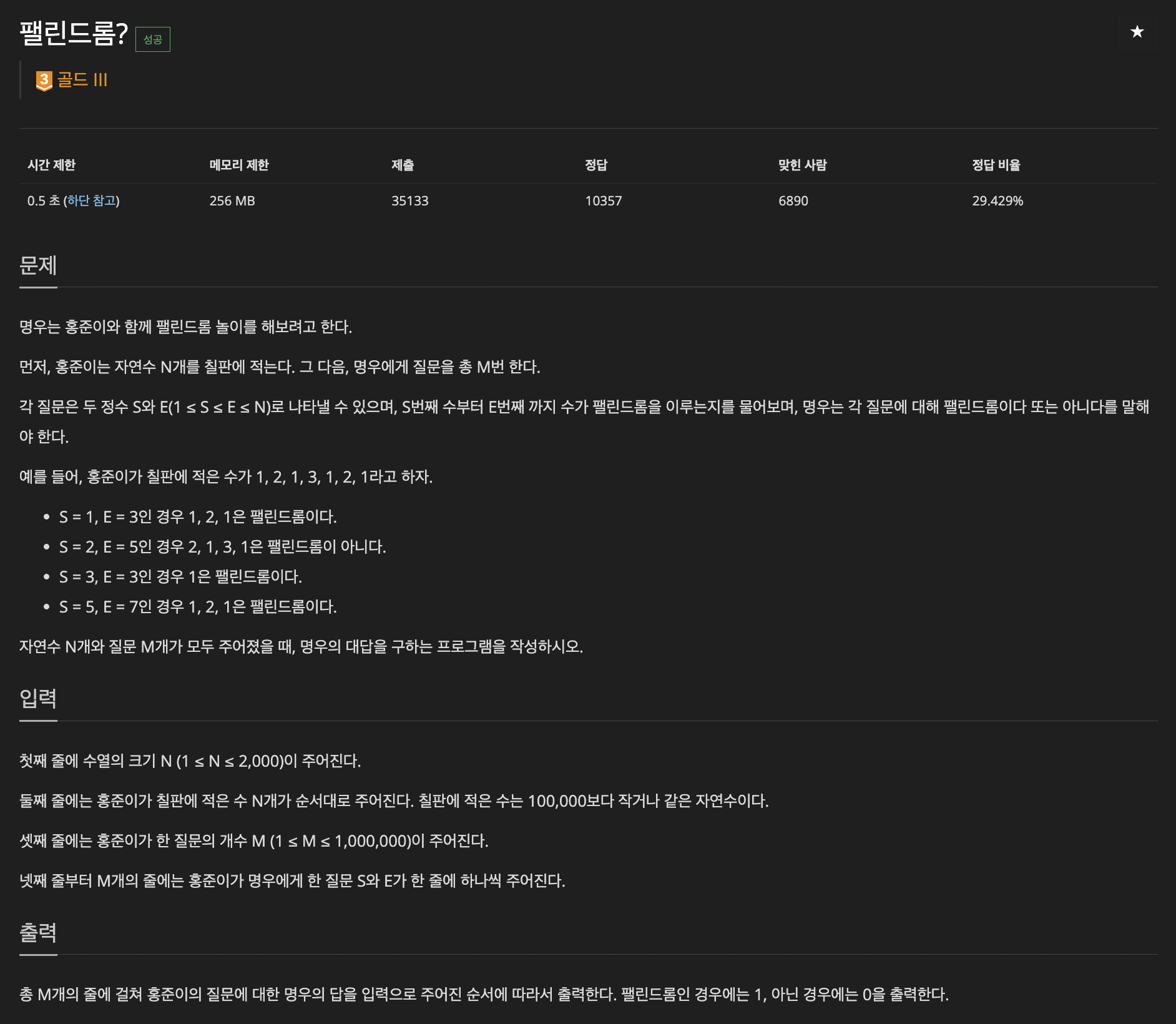
https://www.acmicpc.net/problem/10942

1. 아이디어

• 회문 판단 1번: O(len / 2) (len: 문자열 길이)
• 길이 n 문자열에 대해 회문 판단 m번: O( (n / 2) x m )
  => n, m 최대값 대입: 10^3 x 10^6 = 10^9 >> 2.5억 으로, 시간 초과 !!!
  => DP로 풀이

1) DP 배열 정의: boolean[][] dp

• dp[i][j]: numbers[i] ~ numbers[j] 까지의 수의 회문 여부
  => i: 시작 S, j: 끝 E
  => 행렬 대각선 기준으로 윗 부분만 사용 (헹렬 절반 사용)
  
  

2) 규칙 및 점화식

• 초기식 ①: 행렬 대각선 dp[i][i] = true
  => 숫자 1개인 경우, 무조건 회문

• 초기식 ②: dp[i][i+1] = (numbers[i] == numbers[i+1])
  => 숫자 2개인 경우, 두 숫자의 동일 여부

• 점화식: dp[i][j] = (numbers[i] == numbers[j] && dp[i+1][j-1])
  => 숫자 3개 이상인 경우,
  시작 숫자 numbers[i]와 추가되는 끝 숫자 numbers[j] 동일 여부
  && 시작 숫자와 끝 숫자를 제외한 가운데 숫자들이 회문인지 여부

2. 자료구조

• boolean[][] dp: DP 배열

3. 시간 복잡도

• DP 배열 채우기: 대략 O(n^2)
  => n 최대값 대입: 2,000^2 = 4 x 10^6 << 2.5억

코드

import java.io.*;
import java.util.StringTokenizer;

class Pair {
	public int s, e;

	public Pair (int s, int e) {
		this.s = s;
		this.e = e;
	}
}

public class Main {
	static int n;				// 자연수 개수
	static int[] numbers;
	static int m;				// 질문 개수
	static Pair[] pairs;
	static boolean[][] dp;

	static void solution() {
		for (int i = 1; i <= n; i++) {
			// 초기식 ①: 행렬 대각선 dp[i][i] = true
			dp[i][i] = true;

			// 초기식 ②: dp[i][i+1] = (numbers[i] == numbers[i+1])
			if (i < n)
				dp[i][i+1] = (numbers[i] == numbers[i+1]);
		}

		// 점화식: dp[i][j] = (numbers[i] == numbers[j] && dp[i+1][j-1])
		for (int step = 2; step < n; step++) {
			for (int i = 1; i <= n; i++) {
				if (i + step <= n)
					dp[i][i + step] = (numbers[i] == numbers[i + step] && dp[i+1][i + step -1]);
			}
		}
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(
				new InputStreamReader(System.in)
		);
		StringTokenizer st;

		n = Integer.parseInt(br.readLine());
		st = new StringTokenizer(br.readLine());
		numbers = new int[n + 1];			// [1] ~ [n] 사용
		for (int i = 1; i <= n; i++)
			numbers[i] = Integer.parseInt(st.nextToken());

		m = Integer.parseInt(br.readLine());
		pairs = new Pair[m];
		for (int i = 0; i < m; i++) {
			st = new StringTokenizer(br.readLine());
			int s = Integer.parseInt(st.nextToken());
			int e = Integer.parseInt(st.nextToken());

			pairs[i] = new Pair(s, e);
		}

		dp = new boolean[n + 1][n + 1];		// [1][1] ~ [n][n] 사용
		solution();

		StringBuilder sb = new StringBuilder();
		for (Pair p : pairs) {
			if (dp[p.s][p.e])
				sb.append("1").append("\n");
			else
				sb.append("0").append("\n");
		}
		System.out.println(sb);
	}
}