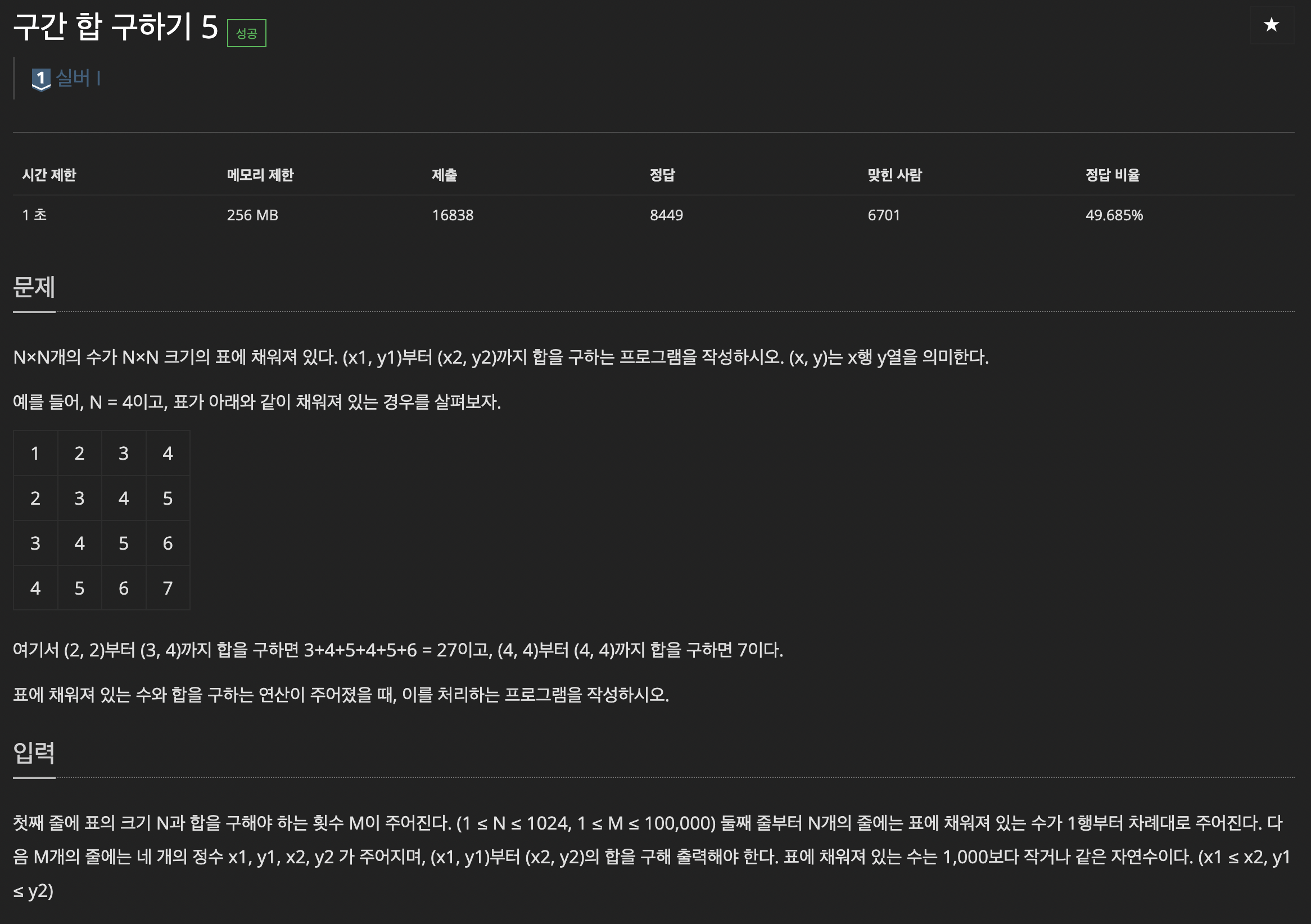
https://www.acmicpc.net/problem/11660
풀이 ① - 각 행마다 누적 합 저장
1. 아이디어
-
입력 행렬을 입력 받으면서, 각 행 마다 누적합을 계산
- 1행 누적합 원소, 2행 누적합 원소, ..., n행 누적합 원소
int[][] sum
-
영역
(x1, y1)~(x2, y2)의 합
= (행x1~x2의 누적합) - (행x1~x2에서 열1~y1-1의 누적합)
= (sum[x1][y2]+ ... +sum[x2][y2]) - (sum[x1][y1 - 1]+ ... +sum[x2][y1 - 1])
주의: 입력 행, 열
(x1, y1),(x2, y2)에서x가 행,y가 열
2. 자료구조
-
int[][] map: 입력 행렬
=> 메모리: n x n x 4 byte
=> n 최대값 대입: 2^20 x 4 byte = 4,194,304 byte ~= 4 MB -
int[][] sum: 각 행마다 누적합
=>sum[i][n]=map[i][1]~map[i][n]까지의 합
=>sum[i][n]의 최대값 = 10^3 x n
=> 최대 10^3 x 1024 << 21억 이므로, int 가능 -
Area[]: 입력 구간(x1, y),(x2, y2)
3. 시간 복잡도
-
입력 영역 1개에 대해 합 계산: for 문으로
x1행 ~x2행 확인
= 대충 O(x2 - x1)
=> Worst 로 첫 행 ~ 마지막 행 확인
= O(n) -
입력 영역 m개에 대해 합 계산 = Worst 로 O(n x m)
=> n, m 최대값 대입: 2^10 x 10^5 = 102,400,000
단순히 테스트케이스마다 매번 일일이 구간의 합을 계산하는 경우
- O(m x n^2)
=> m, n 최대값 대입: 10^5 x 2^20 >> 1억 (시간 초과 발생)
코드
import java.io.*;
import java.util.StringTokenizer;
class Area {
// x가 행, y가 열
public int x1, y1;
public int x2, y2;
public Area(int x1, int y1, int x2, int y2) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
}
}
public class Main_Sum {
static int n; // n x n 행렬
static int m; // 합을 구하는 횟수
static int[][] map;
static Area[] areas; // 입력 구간 (x1, y1), (x2, y2)
static int[][] sum; // 각 행마다 누적합
static StringBuilder sb = new StringBuilder();
static void solution() {
for (Area area : areas) {
int result = 0; // 출력
for (int i = area.x1; i <= area.x2; i++) {
// 1. 행 x1 ~ x2 의 누적합
// = sum[x1][y2] + ... + sum[x2][y2]
result += sum[i][area.y2];
// 2. (행 x1 ~ x2 의 누적합) - (행 x1 ~ x2 에서 열 1 ~ y1-1 의 누적합)
// = (sum[x1][y2] + ... + sum[x2][y2]) - (sum[x1][y1 - 1] + ... + sum[x2][y1 - 1])
if (area.y1 - 1 >= 1)
result -= sum[i][area.y1 - 1];
}
sb.append(result).append("\n");
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(
new InputStreamReader(System.in)
);
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
map = new int[n + 1][n + 1]; // [1][1] ~ [n][n] 사용
sum = new int[n + 1][n + 1];
for (int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
int temp = 0;
for (int j = 1; j <= n; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
temp += map[i][j];
sum[i][j] = temp;
}
}
areas = new Area[m];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
areas[i] = new Area(x1, y1, x2, y2);
}
solution();
System.out.println(sb);
}
}풀이 ② - DP로 이전 값들을 이용하여 누적 합 계산
1. 아이디어
누적 합을 나타내는 DP 배열 이용
1) DP 배열 저장
-
① DP 배열 정의
dp[i][j]:map[1][1]~map[i][j]까지의 누적합 -
② 점화식
dp[i][j]= (dp[i-1][j]+dp[i][j-1]) -dp[i-1][j-1]+map[i][j]
(dp[i-1][j-1]: 중복 부분,map[i][j]: 입력 행렬의 원소)
2) 입력 구간 (x1, y1) ~ (x2, y2)의 합 계산
-
dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]dp[x1-1][y2]: 입력 구간 영역 위dp[x2][y1-1]: 입력 구간 영역 왼쪽dp[x1-1][y1-1]: 중복 부분
주의: 입력 행, 열
(x1, y1),(x2, y2)에서x가 행,y가 열
2. 자료구조
-
int[][] map: 입력 행렬
=> 메모리: n x n x 4 byte
=> n 최대값 대입: 2^20 x 4 byte = 4,194,304 byte ~= 4 MB -
int[][] dp: DP 배열, 영역 누적합
=> 최대 원소값:dp[n][n]= n x n x 10^3 = 2^20 x 10^3 << 21억 이므로, int 가능 -
Area[]: 입력 구간(x1, y),(x2, y2)
3. 시간 복잡도
1) 행렬 map 입력하면서, DP 배열 저장
- O(n^2)
2) DP 배열로 입력 구간의 합 계산
- O(m)
=> 전체 시간 복잡도: O(n^2 + m)
=> n, m 최대값 대입: 2^20 + 10^3 << 1억
단순히 테스트케이스마다 매번 일일이 구간의 합을 계산하는 경우
- O(m x n^2)
=> m, n 최대값 대입: 10^5 x 2^20 >> 1억 (시간 초과 발생)
코드
import java.io.*;
import java.util.StringTokenizer;
class Area {
// x가 행, y가 열
public int x1, y1;
public int x2, y2;
public Area(int x1, int y1, int x2, int y2) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
}
}
public class Main_DP {
static int n; // n x n 행렬
static int m; // 합을 구해야하는 횟수
static int[][] map;
static Area[] areas; // 입력 구간 (x1, y1), (x2, y2)
static int[][] dp; // DP 배열, dp[i][j]: [1][1] ~ [i][j] 까지의 누적합
static StringBuilder sb = new StringBuilder();
static void solution() {
// 2) 각 입력 구간의 합 계산
for (Area area : areas) {
// dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]
int result = dp[area.x2][area.y2]
- dp[area.x1 - 1][area.y2] - dp[area.x2][area.y1 - 1]
+ dp[area.x1 - 1][area.y1 - 1];
sb.append(result).append("\n");
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(
new InputStreamReader(System.in)
);
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
map = new int[n + 1][n + 1]; // [1][1] ~ [n][n] 사용
dp = new int[n + 1][n + 1];
for (int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
// 1) 행렬 map 입력하면서, DP 배열 저장
for (int j = 1; j <= n; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
dp[i][j] = (dp[i-1][j] + dp[i][j-1]) - dp[i-1][j-1] + map[i][j];
}
}
areas = new Area[m];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
areas[i] = new Area(x1, y1, x2, y2);
}
solution();
System.out.println(sb);
}
}