Big-O 빅오 표기법

알고리즘의 성능을 나타내는 표기법
시간 복잡도, 공간 복잡도 예측 시 사용
N의 증가에 따른 처리 시간 또는 필요 공간 계산

| 점근적 표현법 중 하나이며, 일반적으로 상수와 계수를 제거하고 알고리즘의 복잡도를 단순화하여 나타낸다.

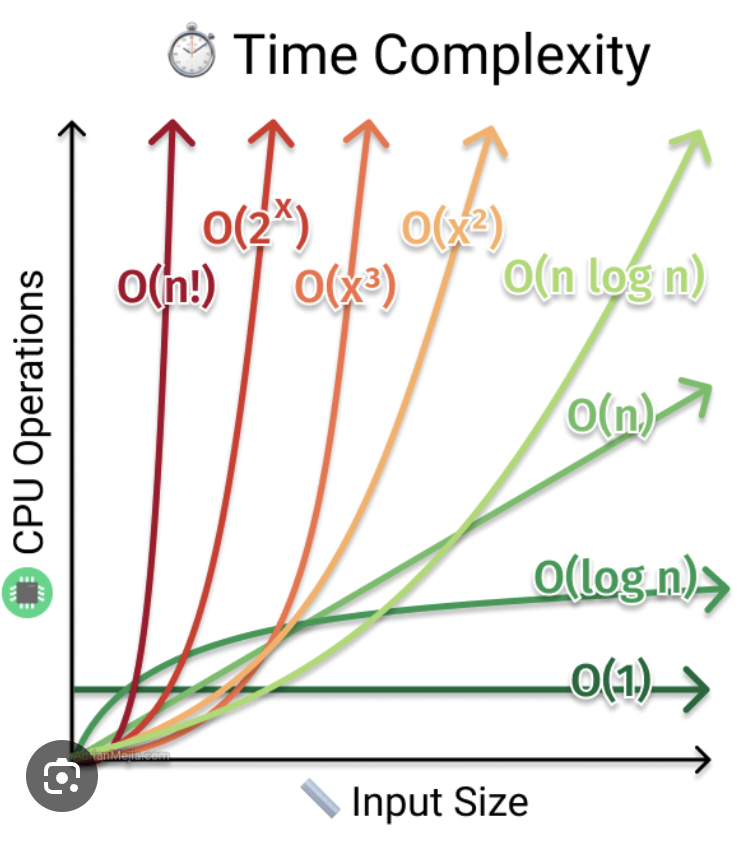
O(1) Constant Time 상수 : input 크기와 상관없이 항상 일정한 시간 소요

arr[0]

O(logn) Logarithmic 로그 : O(1) 다음으로 빠르 시간 복잡도

function logCounter(n) {
  let loopCount = 0;
  for (let i = 2; i <= n; i*=2) {
  	loopCount++;
  }
  return loopCount;
}
logCounter(16) //4

i가 2, 4, 8, 16
output은 1, 2, 3, 4로 증가하여 4를 반환한다.
n은 16이지만 반복문은 4번만 수행한다.
대표적인 알고리즘: 이진탐색 (binary search)

O(n) Linear 선행 : input의 증가 시 같은 비율로 증가

function countCharacters(str) {
  let count = 0;
  for (let i = 0; i < str.length; i++){
  	count++;
  }
  return count;
}

i는 str.length만큼 증가하고 반복문도 str.length만큼 수행한다.
str.length가 증가하는 만큼 반복횟수가 증가한다.
보통 O(n)보다 느린 알고리즘을 비효율적이라고 한다.

O(n^2) Quadratic 제곱 : input 증가 시 n의 제곱 비율로 증가

function buildMatrix(arr) {
	let matrix = [];
    for (let i = 0; i <= arr.length; i++ ) {
    	matrix[i] = [];
        console.log("inner");
        for (let j = 0; j < arr.length; j++) {
        	matrix[i].push(arr[j]);
                    console.log("outer");
        }
    }
    return matrix;
}

(arr.length + 1) * arr.length 만큼 반복문이 수행한다.
input이 증가할 수록 시간도 제곱비율로 증가한다.

O(n!) Factorial 팩토리얼 : 가장 느린 속도, input이 늘어남에 따라 기하급수적으로 증가

function factorial(n) {
  let num = n;
  if (n === 0) return 1;
  for (let i = 0; i < n; i++) {
  	num = n * factorial(n-1);
  }
  return num;
}

Big O 의 규칙

• 최고차항만 표기한다.
• 상수항 & 영향력없는 항은 무시한다.

// O(1)
function printElement(arr, index) {
  console.log(arr[index]); // O(1)
  console.log(arr[index]); // O(1)
  console.log(arr[index]); // O(1)
}
O(1) + O(1) + O(1) = O(1)

// O(n)
function countCharacters(str) {
  let count = 0; //O(1)
  for(let i = 0; i <= str.length; i++){
    count++; // O(1)
  }
  return count; //O(1)
}
O(1) + n * O(1) * O(1) = O(n)


// O(n^2)
function buildMatrix(arr) {
  let matrix = []; //O(1)
  for (let i = 0; i <= arr.lenth; i++){
  	matrix[i] = []; //O(1)
  	for (let j = 0; j < arr.length; j++){
    	matrix[i].push(arr[j]); //O(1)
    }
  }
  return matrix; //O(1)
}
O(1) + n * O(1) * n * (O(1) + O(1) = O(n^2)

Big-O는 인풋의 증가에 따른 연산 처리시간의 증가율을 예측하는 척도

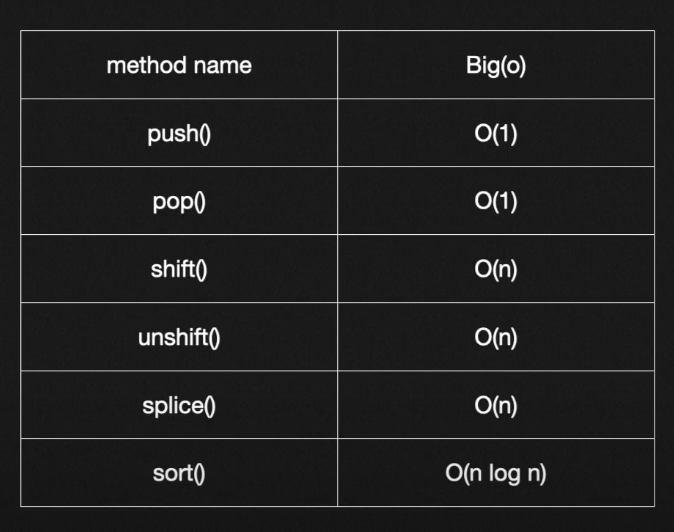
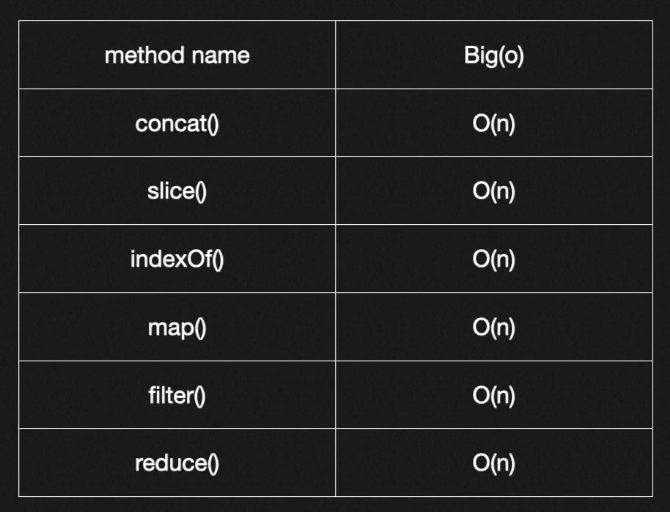
자바스크립트에서 유용한 함수들의 시간복잡ㄷ

참고 https://www.youtube.com/watch?v=5Ky59iblLBI