1. 트리

트리 용어

트리(tree)는 데이터 사이의 계층 관계를 나타내는 자료 구조를 말한다. 계층 관계란 가계도에서 볼 수 있는 부모, 자식, 형제 등의 상호 관계를 의미한다.

용어	설명
노드(node)	O으로 표시. 각각의 노드는 가지로 연결되어 있다.
가지(edge)	—으로 표시. 노드를 연결하는 선들
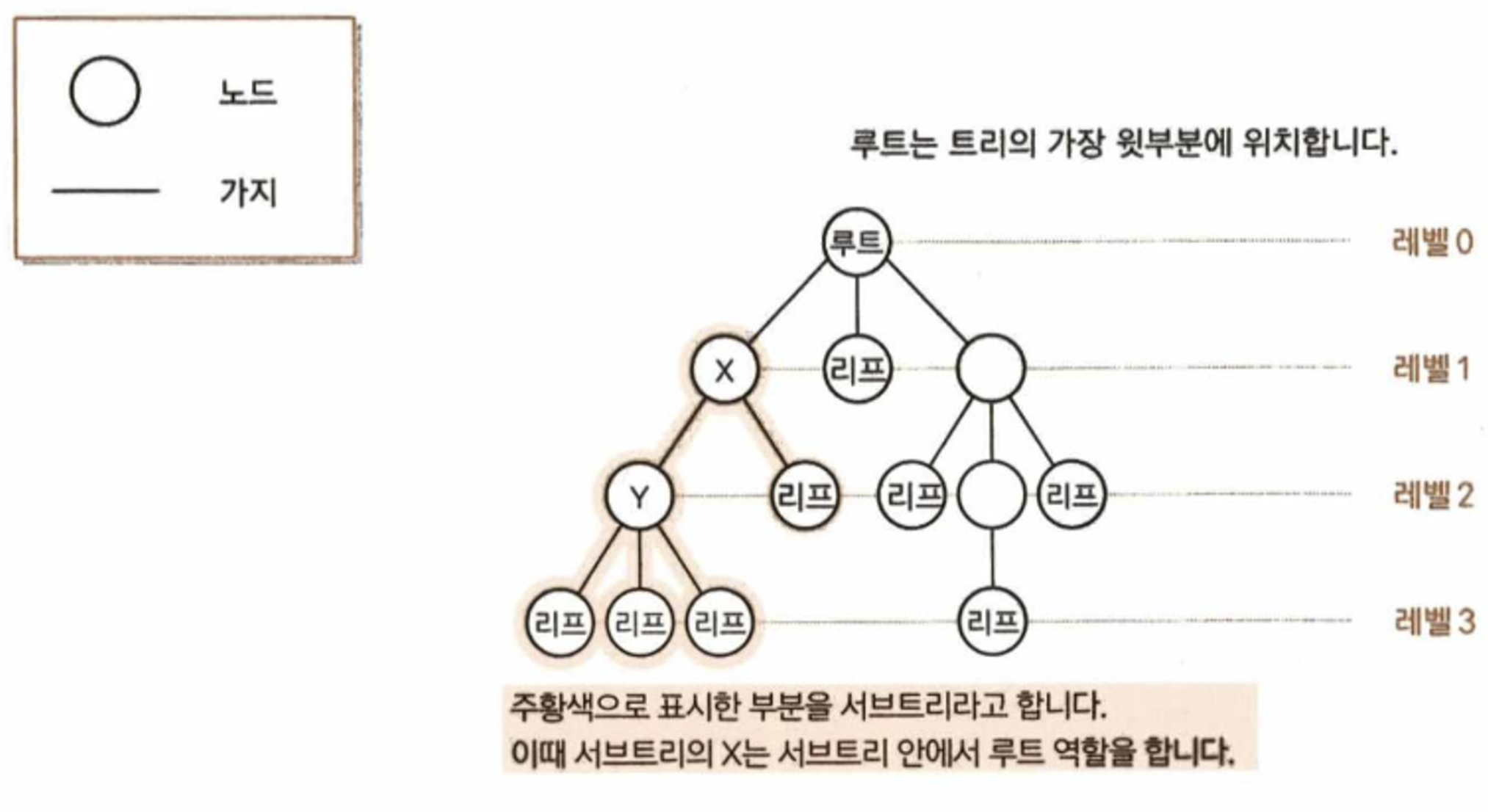
루트(root)	트리의 가장 윗부분에 위치한 노드. 하나의 트리에는 하나의 루트만이 존재
리프(leaf)	트리의 가장 아랫부분에 위치한 즉, 더 이상 뻗어나가지 않는 노드
안쪽 노드(internal node)	리프를 제외한 루트와 나머지 노드들
자식(child)	어떤 노드에서 가지로 연결된 아래쪽 노드를 자식이라고 한다. 노드는 여러 자식을 가질 수 있다.
부모(parent)	어떤 노드에서 가지로 연결된 바로 위쪽 노드. 각 노드는 오직 하나의 부모만 가진다.
형제(sibling)	부모가 같은 노드들
조상(ancestor)	어떤 노드에서 위쪽으로 뻗어 나간 모든 노드를 말한다.
자손(descendant)	어떤 노드에서 아래쪽으로 뻗어 나간 모든 노드를 말한다.
레벨(level)	루트로부터 얼마나 떨어져 있는지를 나타낸 값. 루트 레벨은 0, 루트 기준으로 +1
차수(degree)	노드가 갖는 자식의 수. 모든 노드의 차수가 n이하인 트리를 n진 트리라고 한다.
높이(height)	루트에서 가장 멀리 떨어진 리프까지의 거리(리프 레벨의 최댓값)를 말한다.
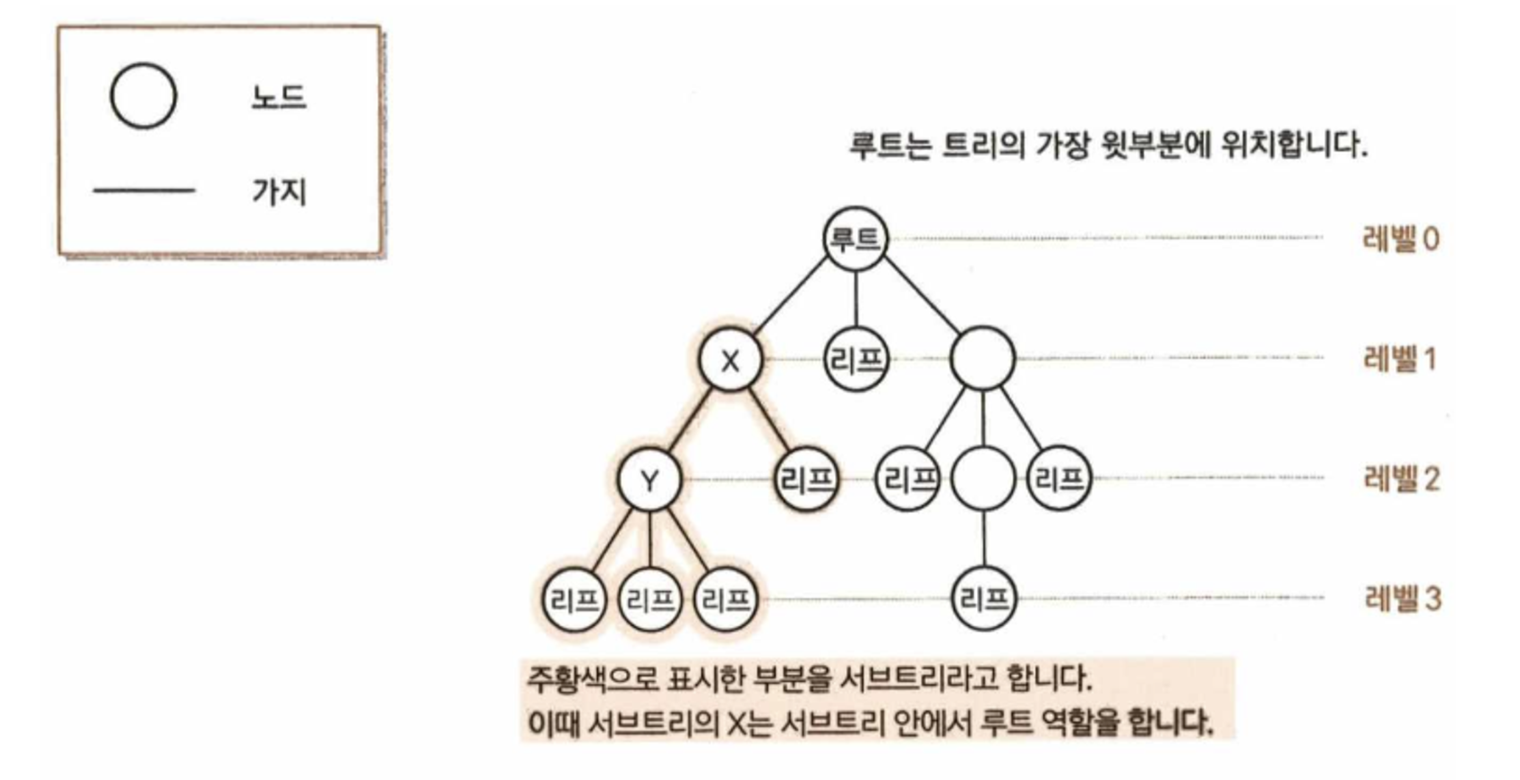
서브트리(subtree)	트리 안에서 다시 어떤 노드를 루트로 정하고 그 자손으로 이루어진 트리
널 트리(null tree)	노드가 전혀 없는 트리

순서 트리, 무순서 트리

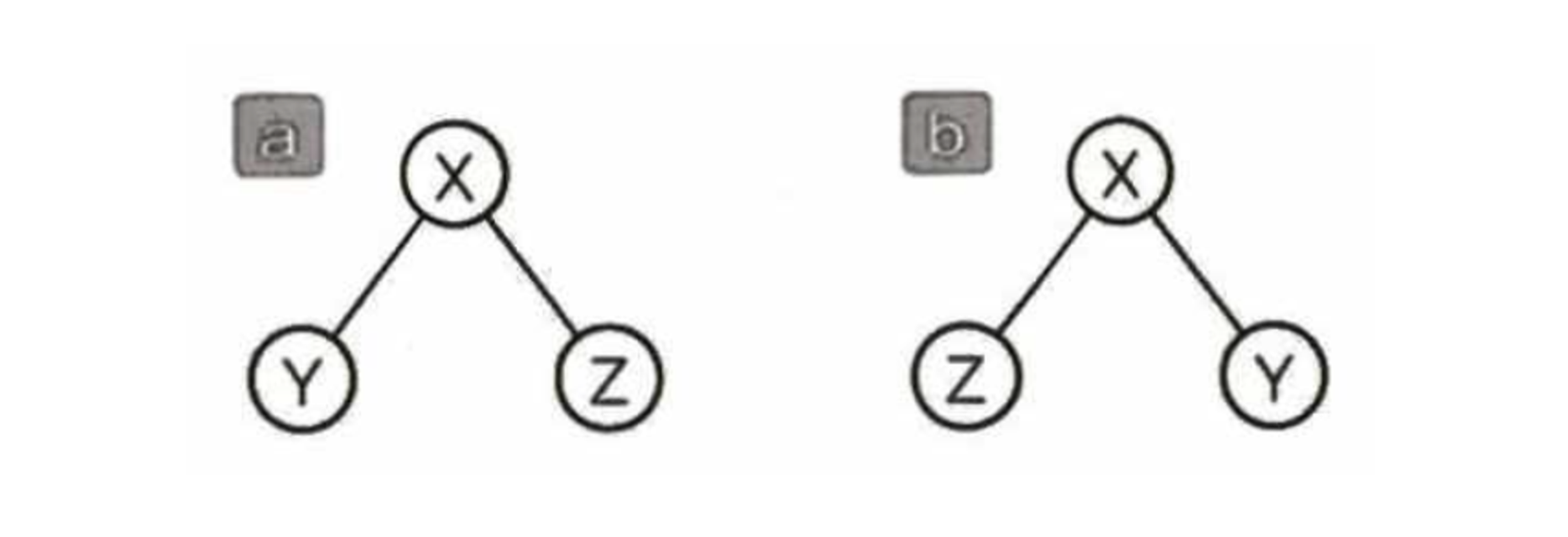
형제 노드 사이의 순서 관계를 따지는지 아닌지에 따라 2종류로 분류할 수 있다. 형제 노드의 순서를 따지면 순서 트리(ordered tree), 따지지 않으면 무순서 트리(unordered tree)라고 한다. 아래의 그림에서 a,b는 순서 트리로 본다면 서로 다른 트리지만 무순서 트리로 본다면 같은 트리라고 할 수 있다.

순서 트리의 탐색 과정

순서 트리의 노드를 스캔하는 방법은 2가지다. 이진 트리를 예로 살펴보자.

BFS: 너비 우선 탐색(가로형)

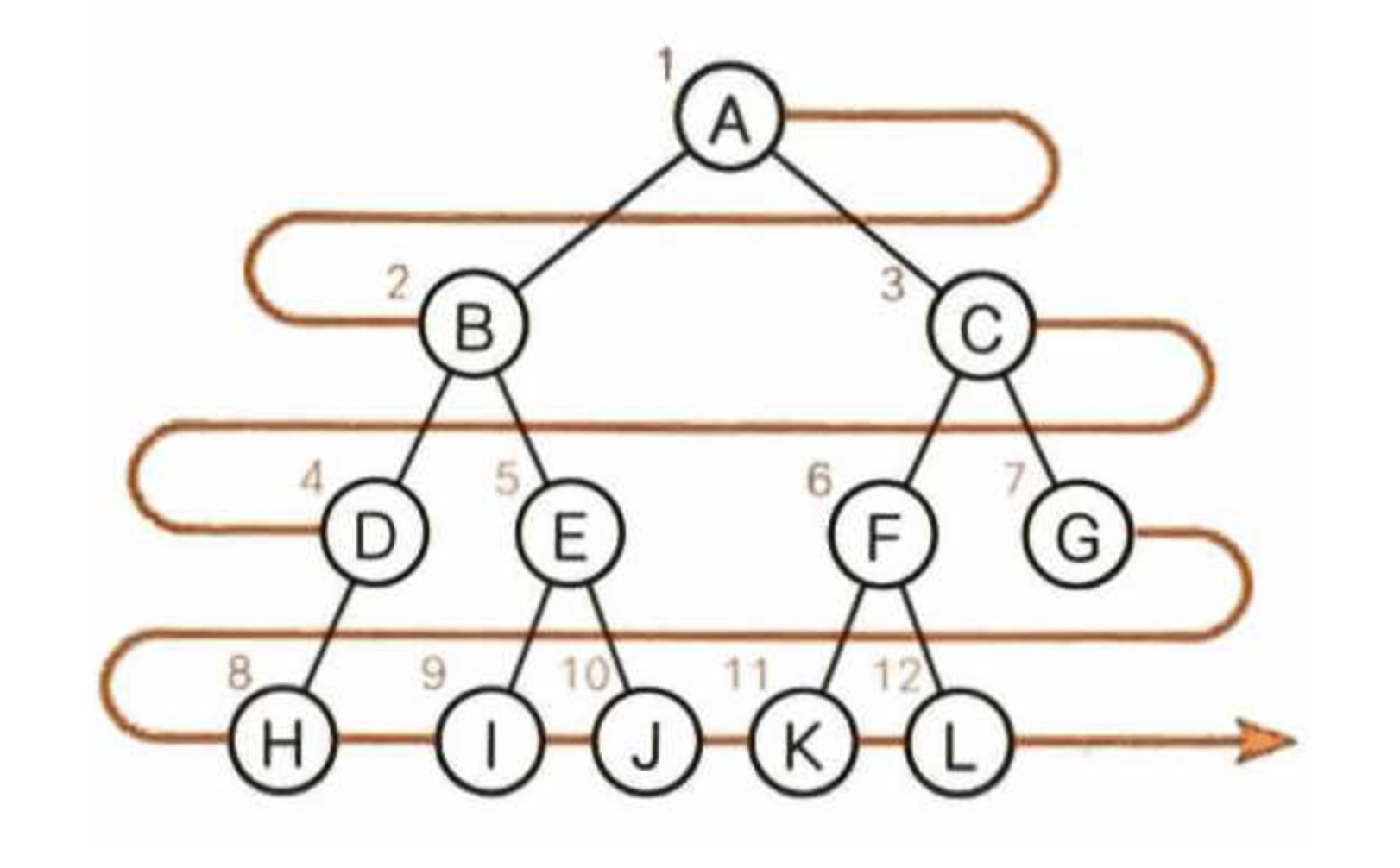
너비 우선 탐색(breadth-first search)은 낮은 레벨에서 시작해 왼쪽에서 시작해 오른쪽 방향으로 따라가다가 한 레벨에서 탐색이 끝나면 다음 레벨로 내려간다. 그림의 탐색 순서는 다음과 같다.

👉 A → B → C → D → E → F → G → H → I → J → K → L

DFS: 깊이 우선 탐색(세로형)

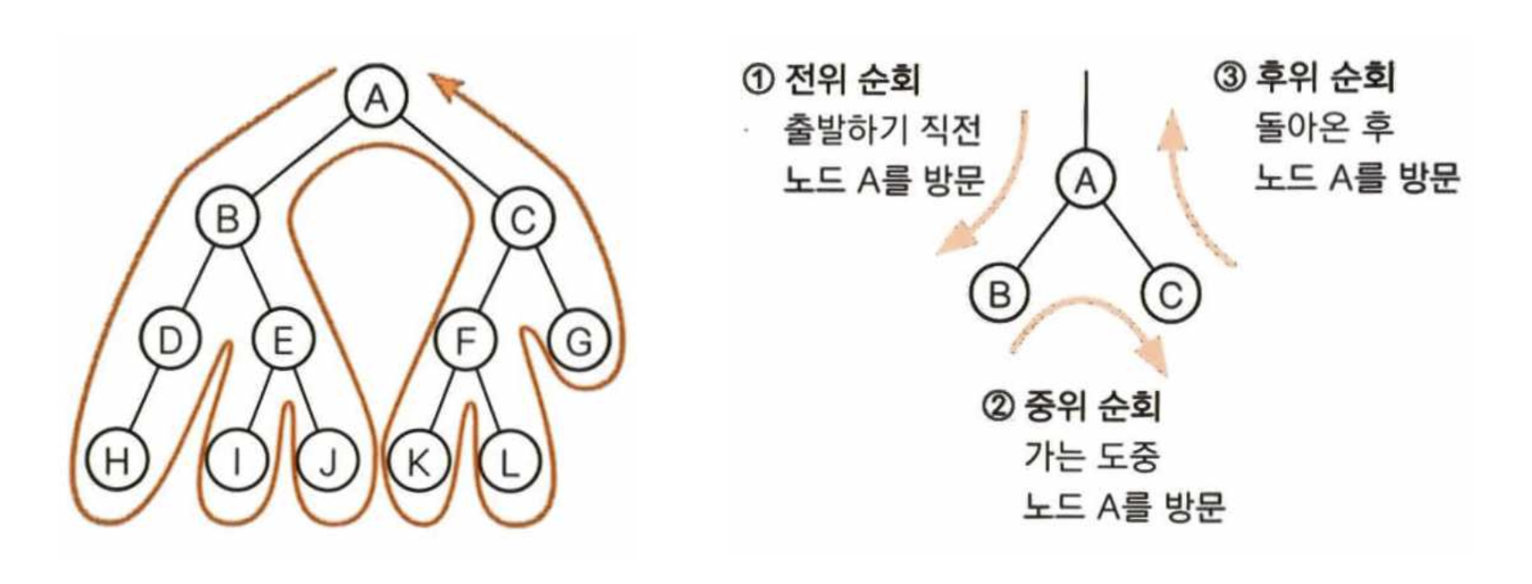
깊이 우선 탐색(depth-first search)은 리프에 이를때까지 아래로 내려가면서 탐색한다. 리프에 도달해 더 이상 탐색할 곳이 없으면 부모에게 돌아간 후 다음 자식 노드로 내려간다. 오른쪽 그림은 A를 몇 번 지나갔는 지를 나타낸 것으로, 깊이 우선 탐색을 진행하면 다음과 같이 노드 A를 3회 지나감을 알 수 있다.

👉 A → B → D → H → E → I → J → C → F → K → L → G

그런데 깊이 우선 탐색을 진행하면서 ‘언제 노드를 방문할지’를 기준으로 아래와 같이 3종류로 구분할 수 있다.

전위 순회(preorder)

‘노드 방문 → 왼쪽 자식 → 오른쪽 자식’ 순서로 깊이 우선 탐색을 진행하며, 전위 순회로 깊이 우선 탐색을 진행하면 다음과 같은 순서로 방문한다. 위에서 예시로 설명한 그림이 바로 전위 순회한 경우이다.

👉 A → B → D → H → E → I → J → C → F → K → L → G

중위 순회(inorder)

‘왼쪽 자식 → 노드 방문 → 오른쪽 자식’ 순서로 깊이 우선 탐색을 진행하며, 다음과 같은 순서로 방문한다.

👉 H → D → B → I → E → J → A → K → F → L → C → G

후위 순회(postorder)

‘왼쪽 자식 → 오른쪽 자식 → 노드 방문’ 순서로 깊이 우선 탐색을 진행하며, 다음과 같은 순서로 방문한다.

👉 H → D → I → J → E → B → K → L → F → G → C → A