GAN loss 정리(언제 다 하지...)

https://github.com/hindupuravinash/the-gan-zoo

Vanila

BCE loss (Binary Cross Entropy) 또는 Adversarial loss

$\min _G \max _D V(D,G)=\mathbb{E}_{x\sim p_{data(x)}} [\log D(x)]+\mathbb{E}_{z\sim p_{z}(z)}[\log (1-D(G(z))],$

where $x\sim P_{data}(x)$: 실제 데이터의 분포, $z\sim P_{x}(x)$: 분포가정(ex. 정규분포)에서 온 latent code의 분포

GAN의 판별자 D는 real or fake를 판단하기 때문에, Binary Cross Entropy(이하BCE)를 사용함. real일 때 y = 1, fake일 때 y = 0 임.

$BCE=-{1\over n}\sum_{i=1}^n (y_i log(p_i)+(1-y_i) log(1-p_i))$를 사용한 loss임.

Wasserstein Objective function

$\min _G \max _D V(D,G)=\mathbb{E}_{x\sim p_{data(x)}} [D(x)]+\mathbb{E}_{z\sim p_{z}(z)}[D(G(z))],$

where $D$는 Lipschitz 조건을 만족하는 함수

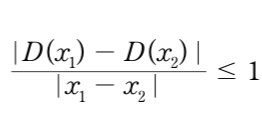
BCE loss의 mode collapse와 vanishing gradient 해결을 위해 등장한 loss임. real일 때 y = 1, fake일 때 y = -1 임.

Conditional GAN loss

$\min _G \max _D V(D,G)=\mathbb{E}_{x\sim p_{data(x)}} [\log D(x|y)]+\mathbb{E}_{z\sim p_{z}(z)}[\log (1-D(G(z|y))].$

BCE loss에 condition으로 label $y$를 걸어주었음. 실제 코드에서는 $x$, $z$에 $y$를 더해주는 식으로 계산함.

---

Style transfer

L1 distance (Manhattan distance)

$\min _G \max _D V(D,G) = \mathcal{L}_{cGAN}+ \lambda \mathcal{L}_{L1}(G).$

$\mathcal{L}_{cGAN}=\mathbb{E}_{y} [\log D(y)]+\mathbb{E}_{x,z}[\log (1-D(G(x,z))].$

$\mathcal{L}_{L1}(G)=\mathbb{E}_{x,y,z}[||y-G(x,z)||_1 ],$

where $y$: real output(ground truth image), $x$: real input

pix2pix에 등장한 loss로, BCE loss(Adversarial loss)만을 사용할 경우 흐린 경우가 발생했음. 이를 해결하기 위해 L1 텀을 추가함.

생성된 이미지와 실제 이미지 사이의 픽셀 간 거리를 구해 이를 최소화하여, 최대한 원본과 가깝게 이미지를 만들어내기 위해 노력함.

Cycle Consistency loss

$\mathcal{L}_{cyc}(G,F)=\mathbb{E}_{x\sim p_{data}(x)} [||F(G(x))-x||_1 ] + \mathbb{E}_{y\sim p_{data}(y)} [||G(F(x))-y||_1 ],$

where $G: X \to Y$, $F: Y \to X$, 이 때 $X\in D_X$, $Y\in D_Y$

unpaired dataset의 경우, paired dataset과는 다르게 좌표가 mapping되는 것이 아님. 따라서 올바른 pair 이미지 생성을 위해 $x$->$y$->$x$와 $y$->$x$->$y$ 를 고려해준 것임. 즉 다른 도메인을 거쳐 원래 도메인으로 돌아왔을 때 최대한 원본의 값을 유지할 수 있도록 함. (아래의 이미지 참고)

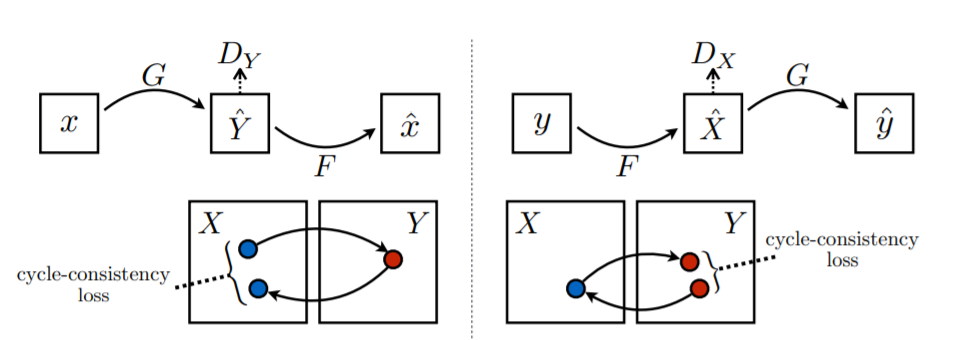
Least Squares loss (Adversarial loss)

$\min _G \max _D V(D,G)_{lsl} = \mathbb{E}_x [(D(x)-1)^2]+\mathbb{E}_z [(D(G(z)))^2]$

BCE loss의 텀에 각각 square를 해준 형태임.
기존의 BCE loss에 비해, 좀 더 안정적으로 학습을 하고 높은 퀄리티의 이미지를 생성할 수 있다고 함.

Identity loss

$\mathcal{L}_{identity}(G,F)=\mathbb{E}_{y\sim p_{data}(y)}[||G(y)-y||_1 ] + \mathbb{E}_{x_{p_{data}}(x)} [||F(x)-x||_1 ],$

where $G: X \to Y$, $F: Y \to X$, 이 때 $X\in D_X$, $Y\in D_Y$

input의 texture는 바꾸되, 분위기나 색상을 유지하기 위해 사용됨. 즉, target domain의 sample이 input으로 들어왔을 때 target domain의 sample을 그대로 내뱉도록 Generator $G$를 regularize 함.

$\it{e.g}$) 오전 그림을 넣었을 때 모델이 해질녘 사진으로 바꾸는 문제가 있었음. 이를 해결하기 위해 사용함.

FACE ID loss

$\mathcal{L}_{face}=\mathbb{E}_{x \sim X_s}[1-\cos(F(x),F(T^i_{s\rightarrow t}(x)))]+[1-\cos(F(x),F(T^i_{t\rightarrow s}(x)))]$

real image와 target domain 사이의 constraints를 더 강화시키기위하여 cosine distance를 이용함.

Group classification loss

$\mathcal{L}_{cls}^{real}=\mathbb{E}_{x \sim \mathcal{Y}_i}[-\log D_t^{cls}(i|x)],$

$\mathcal{L}_{cls}^{fake}=\mathbb{E}_{x \sim \mathcal{Y}_i}[-\log D_t^{cls}(i|T^i_{s\rightarrow t}(x))]$

where $D_t^{cls}(i|x)$는 $D_t$에 의해 계산된 group label 확률분포임

---

업데이트 예정

(SGAN, ACGAN, PGGAN, Style GAN1, Style GAN2, Cycle gan)

Cross-domain Correspondence Learning for Exemplar-based Image Translation

Tell, Draw, and Repeat: Generating and Modifying Images
Based on Continual Linguistic Instruction

---

Multi domain

Multi domain adversarial loss

$\mathcal{L}_{adv} = \mathbb{E}_{x} [\log D_{src}(x)]+\mathbb{E}_{x,c}[\log (1-D_{src}(G(x,c))],$

where $c$ is target domain label

$x$와 target domain label $c$를 이용하여 이미지를 생성함.

Domain classification adversarial loss

$\min _D \mathcal{L}=\mathbb{E}_{x, c'} [-\log D_{cls}(c'|x)].$

real image $x$가 들어왔을 때, original domain label $c'$로 분류를 위한 loss임.

$\min _G \mathcal{L}=\mathbb{E}_{x, c'} [-\log D_{cls}(c|G(x,c))].$

target domain으로 바뀌어 생성된 이미지가 target domain $c$로 분류되기 위한 loss임.

Cycle consistency를 이용한 Reconstruction loss

$\mathcal{L}_{rec} = \mathbb{E}_{x,c,c'}[||x-G(G(x,c),c')||_1 ]$.

Generater $G$가 생성해낸 이미지와 original doamin label $c'$를 input으로 받아, target domain 부분은 변화시키되 input image $x$의 형태를 유지하게끔 복원해내기 위해서 cycle consistence loss를 이용함.

Diversity sensitive loss

$\mathcal{L}_{ds}=\mathbb{E}_{x, Y, z_1, z_2}[||G(x, c_1)-G(x,c_2)||_1 ],$

where Y is target domain

다양한 style을 생성하기 위한 loss임. $c_1$과 $c_2$는 latent vector $z_i \sim Y$에서 생성된 target domain vector를 의미함.

Style reconstruction loss

$\mathcal{L}_{sty}=\mathbb{E}_{x, Y, z}[||c-E_Y G(x,c)||_1 ],$

Generater $G$가 이미지를 생성할 때, c를 이용하도록 함. 단일 Encoder를 통해 여러 도메인에 대해 다양한 출력을 뽑아낼 수 있음. 즉, 얼마나 우리가 원하는 style $c$에 가깝게 이미지를 생성했는가를 판단함.

Conditional Adversarial loss

$\min _G \max _D \mathcal{L}=\mathbb{E}_{x, v, x'} [\log D(x,v,x')]+\mathbb{E}_{x,v}[\log (1-D(x,v,G(x,v)))],$

where $v$ is relative attribute
Conditional GAN의 conditional adversarial loss의 개념을 가져와, 생성 이미지 $G(x,v)$가 realistic하게 보일 뿐만 아니라 $x$와 $G(x, v)$의 차이가 $v$ 일치하도록 함.

Cycle-reconstruction loss

$\min_G \mathcal{L}_{Cycle}=\mathbb{E}_{x,v}[||G(G(x,v),0v)-x||_1 ]$

where $v$ is relative attribute

생성 이미지가 특정 속성을 제외한 모든 측면을 보존하는 것을 보장하기 위함.

Self-reconstruction loss

$\min_G \mathcal{L}_{Self}=\mathbb{E}_{x}[||G(x,0)-x||_1 ]$

where $v$ is relative attribute

v가 0일 경우 생성 이미지가 원본 이미지를 만들어낼 수 있도록 보장함.

Interpolation loss

high-quality interpolation을 위해 보간된 이미지를 realistic하게 보이도록 함.

---

Reenactment

Domain specific perceptual loss

$\mathcal{L}_{perc}(x,y)=\sum_{i=1}^{n}{1\over C_iH_iW_i}||F_i(x)-F_i(y)||_1$

where $F_i \in\mathbb{R}^{C_i \times H_i \times W_i }$

얼굴의 fine details을 살리기위해 사용함. Perceptual loss는 일반적으로 VGG network(target domain에 알맞게 pretrained model로 설정)의 feature map을 사용함.

Reconstruction loss

$\mathcal{L}_{pixcel}(x,y)=||x-y||_1$

perceptual loss만 사용할 경우, 종종 실제와 다른 색을 지닌 이미지를 생성할 경우가 존재함. 이를 방지하기 위해 pixelwise $L_1$ loss를 사용함.

Cross-domain

Feature matching loss

$\mathcal{L}_{feat}=\sum_{l}\lambda_l ||\phi_l(\mathcal{G}(x_A,x'_B))-\phi_l(x_B)||_1$

Domain alignment loss

$\mathcal{L}_{domain}^{l_1}=||\mathcal{F}_{A\rightarrow S}(x_A)-\mathcal{F}_{B\rightarrow S}(x_B)||_1$

Exemplar translation loss

$\mathcal{L}_{perc}-||\phi_l(\hat{x}_B)-\phi_l(x_B) ||_1,$
$\mathcal{L}_{context}=\sum_l \omega_l [-\log ({1 \over n_l} \sum_i \max_j A^l (\phi_i^l (\hat{x}_B), \phi_j^l(y_B)))]$

Correspondence regularization

$\mathcal{L}_{reg}=||r_{y \rightarrow x \rightarrow y}-y_B||_1$

---

Paper

CycleGAN loss (논문 출처)

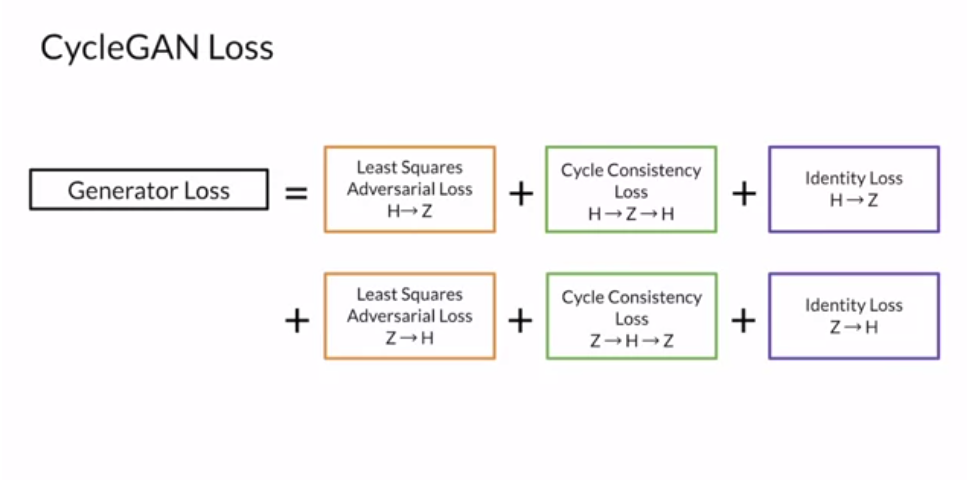
StarGAN loss

$\mathcal{L}_D = -\mathcal{L}_{adv}+\lambda_{cls} \mathcal{L}^{r}_{cls}$
$\mathcal{L}_G = \mathcal{L}_{adv}+\lambda_{cls} \mathcal{L}^{f}_{cls} + \lambda_{rec}\mathcal{L}_{rec}.$

$\mathcal{L}_{adv} = \mathbb{E}_{x} [\log D_{src}(x)]+\mathbb{E}_{x,c}[\log (1-D_{src}(G(x,c))],$

where $c$ is target domain label

StarGAN2 loss

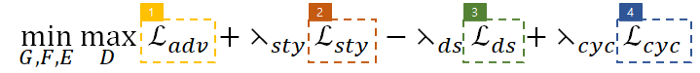
RelGAN loss

: loss functoin이 G 1개와 D 3개 {$D_{Real}, D_{Match}, D_{Interp}$} 로 구성됨.

사전 지식

• n차원 속성 벡터 $a$ = $[a^{(1)}, a^{(2)}, . . . ,a^{(n)}]^{T}$
• 각 특징 $a^{(i)}$는 의미있는 특성 (ex> 얼굴 이미지의 나이, 성별, 머리색 등)
• RelGAN의 목적 : input 이미지 x를 target 특징을 가지면서 real같아 보이는 output 이미지 y로 출력 (몇 개의 user가 지정한 특성은 원래 이미지와 다르게, 그 외는 특성이 유지되도록 출력)
• mapping function $(x, v) → y$를 학습할 것을 제안
  • $v$ : 속성의 변화를 원하는 상대 속성 벡터

상대 속성?

• 이미지 x의
  특징 벡터 $a$ = 원래 도메인,
  target 특징 벡터 $\hat{a}$ = target 도메인

• $a$, $\hat{a}$는 둘 다 n차원 벡터임.

• $a$와 $\hat{a}$ 사이의 상대 속성 벡터
  
  

• input 이미지 x를 output 이미지 y로 매핑할 때 user가 원하는 속성 변경을 나타냄.

ex> 이미지 특성이 이진값 (0 or 1)이면 상대 속성은 (−1, 0, 1) 3개의 값으로 표현됨.
: 각 값은 이진 속성에 대한 user의 action에 해당

turn on	+1
turn off	-1
unchanged	0

• 즉, 상대 속성은 user의 요구사항을 인코딩 하는 것으로 해석 가능.

• 상대 속성을 통한 얼굴 속성 보간
  : $x$와 $G (x, v)$ 사이의 보간을 수행하려면 $G (x, \alpha{v})$를 적용하기만하면 됨. ($\alpha ∈ [0, 1]$은 보간 계수)
  

(1) Adversarial Loss

• 생성된 이미지를 real 이미지와 구별할 수 없도록 standard GAN의 adversarial loss 적용.

• x : real 이미지
• v : 상대 속성
• $D_{real}$ : 실제 이미지와 생성된 이미지 구분, unconditional discriminator

(2) Conditional Adversarial Loss

1. output 이미지 $G(x, {\alpha}v)$가 realistic해 보이길 원함
2. $x$ 와 $G(x, {\alpha}v)$의 차이가 상대 속성 $v$와 match 되어야 함.

• $D_{match}$
  : cGAN의 컨셉을 도입한 discriminator (conditional discriminator)
  : real triplet $(x, v, x')$ 과 fake triplet $(x, v, G(x, v))$을 input으로 함.
  

• real triplet $(x, v, x')$
  : 2개의 real 이미지 $(x, x')$와 상대 속성 벡터 $v (= a-a')$로 구성

• $a$와 $a'$
  : 각각 x와 $x'$의 속성 벡터

• x와 $x'$
  : 다른 속성을 가진 unpaired한 training data (real 이미지)
  

---

(참고)

• conditional GAN loss
  

$ G^* = arg minG max_D L{cGAN} (G, D) $

(출처 : Image-to-Image Translation with Conditional Adversarial Networks)

---

• real triplet
  : real 이미지 2개 & 잘 matched 상대 속성

• fake triplet
  : real 이미지 1개 & fake 이미지 1개 & 잘 matched 상대 속성?????????

• $(x, x')$와 mismatched $v$로 구성되는 wrong triplet을 추가
  (input-output 쌍이 상대 속성과 일치하는지 여부를 결정하는 matching aware discriminator에 영감 받음)
  + wrong triplet
  : real 이미지 2개 & 잘못 matched 상대 속성
  : wrong triplet을 추가함으로써 $D_{match}$는 아래처럼 분류하려고 함.

triplet	분류
real triplet	+1
fake triplet	-1
wrong triplet	-1

•  wrong triplet 작동 방식  

  $(x, v (= a-a'), x')$로 표현되는 real triplet이 주어지면,
  4개의 변수 중 하나를 wrong triplet에 의해 생성되는 것으로 대체함으로써
  4개의 wrong triplet을 얻는다.
  

(3) Reconstruction Loss

• unconditional loss와 condtional loss를 최소화하면서 G는 output 이미지 $G(x, v)$를 real 이미지처럼 생성하는 것을 학습함.
• 그리고 $x$와 $G(x, v)$의 차이는 상대 속성 $v$에 match됨
• 그러나, G가 low level (ex> 배경 표현) -> high level (ex> 얼굴 이미지의 identity) 과정에서
  다른 모든 부분을 유지하면서 속성과 관련된 contents만 수정한다는 보장이 없다.
• 이 문제를 보완하기 위해 G를 규제하는 cycle-reconstruction loss와 self-reconstruction loss를 도입함. (둘 다 L1 norm 사용)

1) Cycle-reconstruction loss

• cycleGAN의 cycle consistency 개념을 적용
• L1 norm 사용
  

: $G(:, v)$, $G(: ,−v)$는 서로의 역이 됨.

---

(참고)

• cycleGAN의 cycle consistency
  

출처) Unpaired
image-to-image translation using cycle-consistent adversarial networks

---

2) Self-reconstruction loss

• 상대 속성 벡터가 $0$ 벡터인 경우, 아무 속성도 변하지 않았음을 의미
• output 이미지 $G(x, 0)$은 가능한 한 $x$에 가깝게 돼야 함.
• 아래의 loss를 통해 구현 가능

• G는 auto-encoder로 다시 돌아가서(degenerate) $x$를 재구성함.
• L1 norm 사용

(4) Interpolation Loss

• G는 $G(x, {\alpha}v)$ ($\alpha ∈ [0, 1]$은 보간 계수) 를 통해
  이미지 $x$와 변환된 이미지 $G(x, v)$ 사이를 보간함.
• 보간의 high-quality를 위해 보간된 이미지 $G(x, {\alpha}v)$를 realistic하게 보이기를 원함.
  -> "$G(x, {\alpha}v)$"를 보간되지 않은 output 이미지인 "$G (x, 0)$ 및 $G (x, v)$"와 구별할 수 없도록 만드는 규제를 제안
  = interpolation discriminator $D_{Interp}$
• $D_{Interp}$의 목적
  : 생성된 이미지를 input으로 받아 보간 정도 $\hat{\alpha}$를 예측 ($\hat{\alpha} = min(\alpha, 1-\alpha)$)
  : $\hat{\alpha}$를 예측함으로써 $\alpha$와 $1-\alpha$ 사이의 모호성을 해결
  + $\hat{\alpha}$ = 0 : 보간 x
  + $\hat{\alpha}$ = 0.5 : 최대 보간
  

• 첫번째 term
  : $G(x, {\alpha}v)$로부터 $\hat{\alpha}$를 복구
• 두번째, 세번째 term
  : $D_{Interp}$이 보간되지 않은 이미지에 대해 0을 출력

---

• 그런데, 실험적으로 아래의 수정된 $D_{Interp}$ loss가 학습을 더 안정화 시키는 것을 발견했음.

(Ⅱ['] : argument가 참이면 1, 아니면 0인 indicator function)

---

• G는 아래의 loss 추가

• G는 $G(x, {\alpha}v)$가 보간되지 않았다고 생각하도록 $D_{Interp}$를 속임.

• $L_{Interp}^{D}$와 $L_{Interp}^{G}$ 과정

(5) Full Loss

• 훈련을 안정화하기 위해 loss function에 orthogonal regularization ($L_{Ortho}$)을 추가했음.
• D = {$D_{Real}, D_{Match}, D_{Interp}$} 와 G에 대한 각각의 full loss function

($\lambda_{1}$, $\lambda_{2}$, $\lambda_{3}$, $\lambda_{4}$, $\lambda_{5}$는 hyper-parameters)

Loss	Generator L	Discriminator L
Adversarial Loss	$L_{Real}$	$L_{Real}$
Conditional Adversarial Loss	$L_{Match}^{G}$	$L_{Match}^{D}$
Interpolation Loss	$L_{Interp}^{G}$	$L_{Interp}^{D}$
Reconstruction Loss	$L_{Cycle}$
Reconstruction Loss	$L_{Self}$
orthogonal regularization	$L_{Ortho}$

논문) RelGAN: Multi-Domain Image-to-Image Translation via Relative Attributes

SGAN (Semi-Supervised Learning GAN)

• DCGAN 기반

ACGAN (Auxiliary Classifier GAN)

* standardGAN

• D는 $X_{real}$들어갔을 때 Source = real일 확률 + $X_{fake}$들어갔을 때 Source = fake일 확률을 maximize하도록 훈련함.
• G는 $X_{fake} = G(z)$를 생성
• $P(S | X) = D(X)$

* ACGAN

• framework

• 목적함수는 2개로 구성
  : 맞춘 source의 log-likelihood $L_S$ / 맞춘 class의 log-likelihood $L_C$

• D는 $L_S+L_C$를 maximize하도록, G는 $L_S-L_C$를 maximize하도록 훈련

• 모든 생성된 샘플에는 기존의 noise z에 더해 해당 class label $c$~$p_c$가 있음.
• G는 $X_{fake} = G(c,z)$를 생성

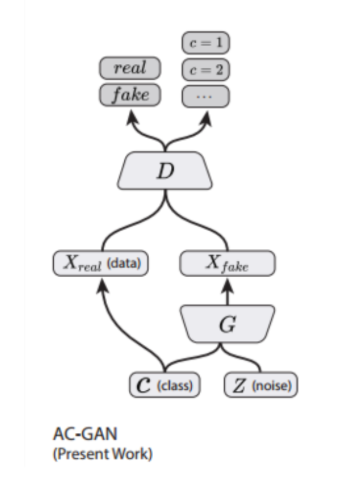
• input : class 임베딩 & noise 벡터
• output : 이진 분류기 (real/fake) & multi-class 분류기 (이미지 class)

(출처 : https://stephan-osterburg.gitbook.io/coding/coding/ml-dl/tensorfow/chapter-4-conditional-generative-adversarial-network/acgan-architectural-design)

논문) Conditional Image Synthesis with Auxiliary Classifier GANs

PGGAN (Progressive Growing of GANs)

• G와 D는 거울구조를 가짐.
  

• WGAN-GP(Gradient Penalty) loss 사용 + 미니배치 당 G와 D의 최적화를 번갈아가면서 함. ($n_{critic}=1$)
  
  
  (이때, gp는 loss function이 수렴하는데 영향을 주지 않음)

• WGAN의 weight clipping은 Lipschitz 제약을 적용해서 종종 poor samples을 생성하거나 수렴에 실패하는 경우 발생
  → weight clipping 대신 critic의 weight에 penalty를 준 것이 WGAN-GP

• 추가적으로 discriminator의 output이 0으로부터 너무 멀리 떨어지는 것을 방지하기 위해 discriminator loss에 4번째 term을 넣음
  

(참고)

• WGAN-GP에서 $n_{critic}=1$로 둔다는 것
  

(Critic : GAN의 discriminator와 유사한 역할)

논문) D2PGGAN: TWO DISCRIMINATORS USED IN PROGRESSIVE GROWING OF GANS
논문) Wasserstein GAN
논문) PROGRESSIVE GROWING OF GANS FOR IMPROVED QUALITY, STABILITY, AND VARIATION
참고) https://study-grow.tistory.com/entry/Deep-learning-%EB%85%BC%EB%AC%B8-%EC%9D%BD%EA%B8%B0-StyleGAN-loss-%EC%9D%B4%ED%95%B4-%EC%96%95%EA%B2%8C-%EC%9D%BD%EB%8A%94-WGAN-WGAN-GP

StyleGAN1

• discriminator, loss function을 수정하지 않고 generator의 architecture만 수정했음.
• Style-based generator architecture
  

• style-based G는 input latent z를 intermediate latent vector v로 임베딩함으로써 특징들이 선형적으로 잘 분리된 상태가 되게 함.

• G에 직접적으로 noise를 넣어줌으로써 생성된 이미지의 stochastic 변형(ex>주근깨, 머리)으로부터 high-level 특징(포즈, identity)을 자동으로 분리할 수 있음.

• affine 변환을 통해 w를 styles $y = (y_s, y_b)$로 구체화하고 synthesis network의 각 conv layer 후에 AdaIN 정규화를 수행함.

• WGAN-GP loss 사용했음 (그대로)

논문) A Style-Based Generator Architecture for Generative Adversarial Networks

CycleGAN

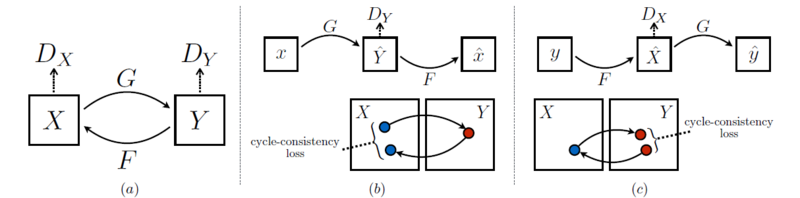
(1) Adversarial loss

* X → Y인 경우

:

* 반대로 Y → X인 경우

: $L_{GAN}(F,D_X,Y,X)$

• X 도메인에서 Y 도메인으로 매핑하고 역매핑도 해야 하므로 2개의 generator를 사용했고 도메인이 2개니까 2개의 discriminator 사용 (도메인의 수만큼 G, D 수 정해짐)

(2) Cycle-consistency loss

• x → G(x) → F(G(x)) ≈ x / y → F(y) → G(F(y)) ≈ y
• 한 도메인이 다른 도메인으로 갔다가(생성) 원래 도메인으로 잘 복원하도록 함.
• 즉, 이미지의 도메인(스타일)을 바꾸되, 다시 원본으로 복원 가능한 정도로만 바꾸는 것

(3) Full loss

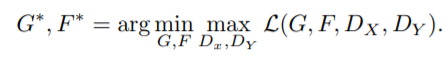
+ (4) Identity loss

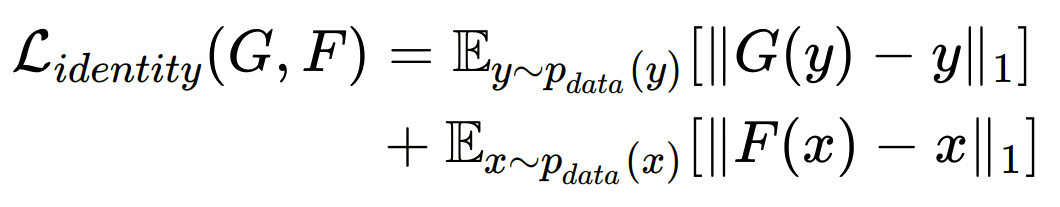
• input과 output의 색감 유지를 위해 도입
• target 도메인 Y가 input으로 들어왔을 때, 동일한 Y 도메인으로 매핑하는 경우 차이가 적도록해 도메인 Y의 색감을 유지할 수 있도록 한다.

논문) Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks