Introduction to Causal Inference: Lecture 3 Graphical Models

Brady Neal의 introduction to causal inference 리뷰입니다.
youtube: https://www.youtube.com/watch?v=Go4EkHN_PcA&list=PLoazKTcS0Rzb6bb9L508cyJ1z-U9iWkA0&index=19
material: https://www.bradyneal.com/causal-inference-course
My article will be uploaded to https://www.notion.so/GNN_YYK-0303f11d4fa0433792562333dea173a3.

3.1 Graph Terminology

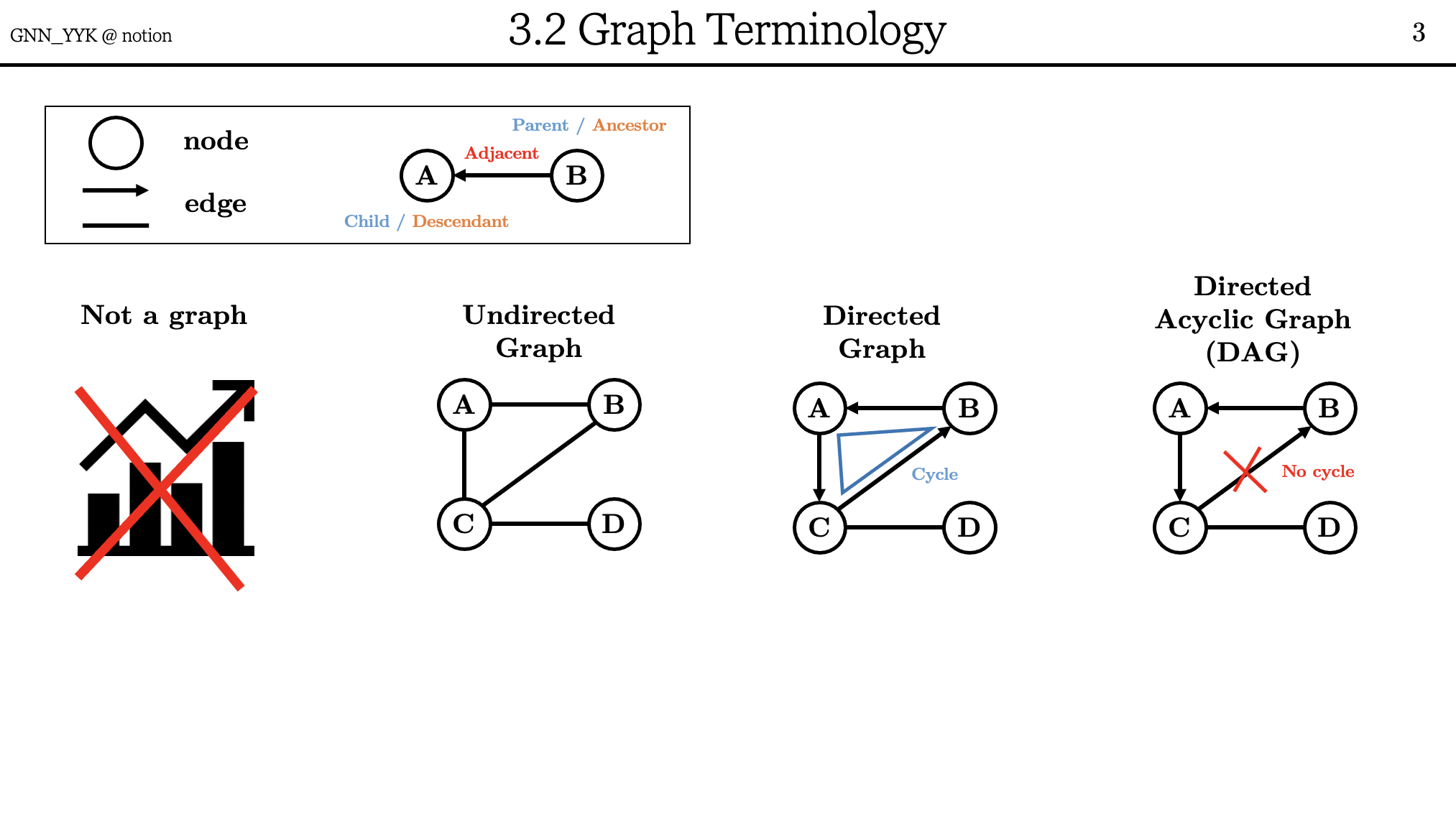
그래프라는 단어를 들었을 때, 흔히 scatter plot이나 bar plot과 같은 시각적인 그림을 떠올리는 경우가 많습니다. 그러나 앞으로 강의에서 말하는 그래프는 node와 edge들의 set을 의미합니다.

그래프에서 사용되는 몇 가지 용어들을 짧게 살펴봅시다. (path와 cycle은 생략함.)
방향성이 없는 edge로 이루어진 그래프를 undirected graph, 방향성이 있는 edge로 이루어진 그래프를 directed graph라고 합니다. 이 때 cycle이 없는 directed graph를 directed acyclic graph라고 하는데, 줄여서 DAG(강의에서는 대-그라고 읽음.)라고 표현합니다.

앞으로 설명할 bayesian networks에서 그래프(혹은 네트워크)는 DAG를 기본으로 합니다.

---

3.2 Bayesian Networks

Causal graphical models은 probabilistic graphical models(pgm) 분야 중 하나입니다. Bayesian network는 pgm 중에 하나로, causal graphical models(causal bayesian network)의 특성을 가지고 있습니다. Bayesian network가 무엇이고, 어떻게 쓰이는지에 대해 알아보겠습니다.

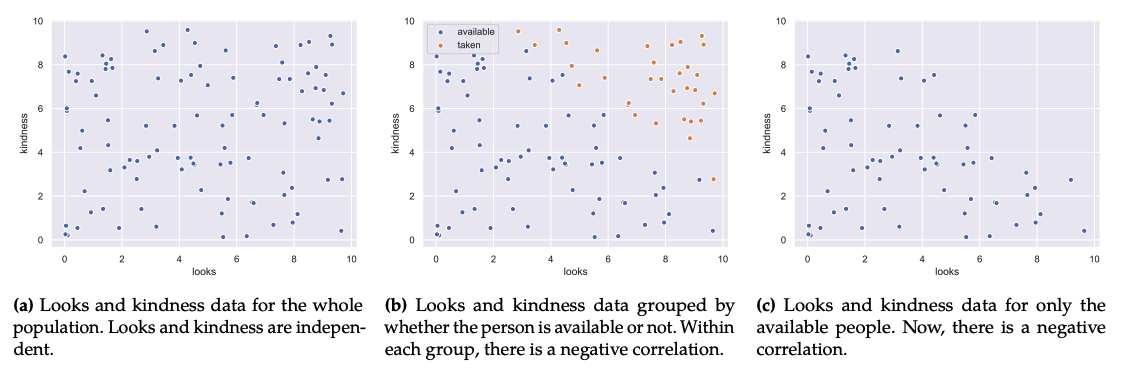
우리는 일반적으로 data의 분포 $P(x_1, x_2, ..., x_n)$을 알고자 합니다. 일반적으로 chain rule을 적용하여 표현하면 다음과 같습니다.

$P(x_1, x_2, ..., x_n)=P(x_1) \prod_i P(x_i|x_i-1, ..., x_1)$

그러나, parameter가 증가할수록 계산해야 하는 양이 exponential하게 증가하기 때문에, 모든 경우를 구하는 것은 intractable할 수 있습니다. 위 그림의 예시에서 $x_i$가 binary case라고 했을 경우, $p(x=1)=1-p(x=0)$ 구할 수 있기 때문에 $2^{n-1}$의 계산이 요구 됩니다.

joint distribution을 좀 더 효율적으로 구하는 방법 중 한가지는 가정을 하는 것입니다. 여기서 Local Markov Assumption이 등장하게 됩니다.

Assumption 3.1 (Local Markov Assumption) Given its parents in the DAG, a node $X$ is independent of all its non-descendants.

Local Markov Assumption은 DAG에서 parents가 주어지면 모든 non-descendants와 독립을 가정하는 것입니다.
즉, 위의 이미지에서와 같이 $P(x_4|x_3,x_2,x_1)$가 $P(x_4|x_3)$로 대체될 수 있습니다.

즉 DAG에서 Local Markov Assumption을 통해 bayesian network가 등장하게 됩니다. 이때 각각의 그래프 G에 각각의 node들은 P에 각각의 random variable이 one-to-one mapping 되는 것입니다.

Bayesian network에 등장하는 Bayesian Network Factorization를 살펴봅시다.

Definition 3.1 (Bayesian Network Factorization) Given aprobability distribution $P$ and a DAG $G$, P fatorizes according to $G$ if
$P(x_1,...,x_n)=\prod_i P(x_i|\mathsf{pa}_i)$

Bayesian Network Factorization은 bayesian network의 chain rule 혹은 Markov compatibility로도 불립니다.
만약 $P$가 위 그림의 graph에 대하여 Markor라면, Bayesian Network Factorization를 사용하여 $P$의 joint distribution이 아래와 같이 표현됩니다.

$P(x_1, x_2, ..., x_n)=P(x_1)P(x_2)P(x_3|x_2, x_1)P(x_4|x_3)$

($P$ is Markov with respect to the graph in Figure 라고 표현합니다.)
만약 그림에서 그래프가 더 sparse하다면, joint distribution이 더욱 simple해질 것입니다.

우리는 Bayesian Network Factorization가 결국 Local Markov Assumption와 equivalent임을 알 수 있습니다.
자세한 증명은 Koller and Friedman(2009)에서 확인할 수 있습니다. 저는 넘어가도록 하겠습니다 : )

Bayesian network에서 causal network로 가기 위해 매우 중요한 assumption에 대해 살펴보겠습니다.

조금 혼란스러울수도 있지만, Local Markov Assumption에서는 만약 노드 $X$와 $Y$가 인접(adjacent)했을 때, $X$와 $Y$가 dependent한 것을 의미하지 않습니다. 반면 causal inference에서는 $X\rightarrow Y$의 경우 인과관계가 있다고 하죠. 따라서 Bayesian network에서 추가적인 assumption이 필요한 것을 알 수 있습니다.

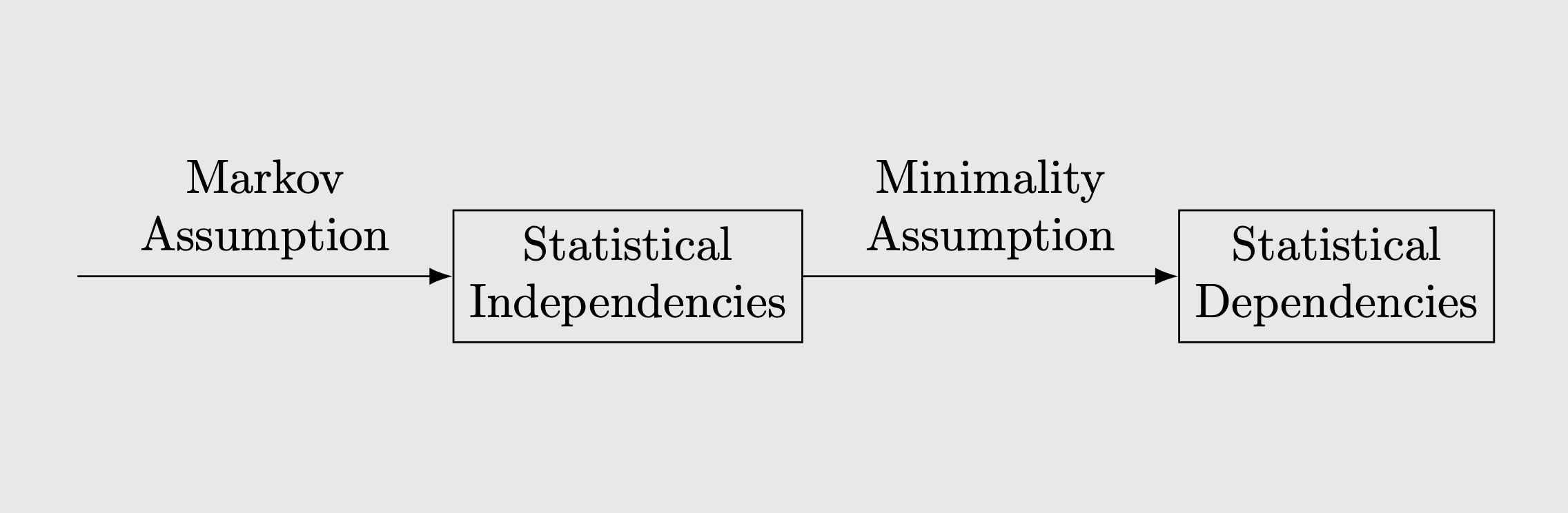
인접한 노드 사이의 dependence를 보장하기 위해, local Markov assumption보다 더 강력한 assumption이 필요합니다.

Assumption 3.2 (Minimality Assumption)
1. Given its parents in the DAG, a node $X$ is independent of all its non-descendants (Assumption 3.1)
2. Adjacent nodes in the DAG are dependent.

예를 들어, $X\rightarrow Y$가 있다고 해봅시다. local Markov assumption을 통해 우리는 $P(x,y)=P(x)P(y|x)$이라고 할 수 있습니다. 그러나 이때 역시 $P(x,y)=P(x)P(y)$을 정의할 수 있습니다. 즉 인접한 두 노드 $X, Y$가 독립이라고 할 수 있습니다. 반면에 minimality assumption을 통해 $P(x,y)=P(x)P(y|x)$로 factorize 할 수 있습니다.

3.3 Causal Graphs

Causal 관계를 보장하기 위한 한 가지의 가정이 추가적으로 등장합니다.

Assumption 3.3 ((Strict) Causal Edges Assumption)
In a directed graph, every parent is a direct cause of all its children.

Assumption 3.3을 통해 부모 노드와 자식 노드 간의 종속성을 가정했기 때문에 Assumption 3.3이 Assumption 3.2(minimality)를 반영하고 있다고 할 수 있습니다.

반면에 non-strict causal edges assumption이 존재하는데, 이는 몇몇의 부모 노드들이 자식 노드에 영향을 미치지 않는 것을 의미합니다. 실제로 Causal graph에서 항상 부모가 자식에게 영향을 미치는 것은 아닙니다. 확실히 하기위해, 앞으로 언급하게 될 Causal graph는 strict causal edges assumption을 만족하는 DAG라고 하겠습니다.

3.4 Two-Node Graphs and Graphical Building Blocks ~ 3.5 Chains and Forks

Basic assumption과 definition을 봤으니, 이제부터 3장의 핵심인 the flow of association과 causation in DAGs에 대해 살펴보겠습니다.

Flow of association은 그래프 안의 두 노드가 연결되었는지, 아닌지를 의미합니다. 즉 statistically 독립인지 종속인지를 의미합니다.

그래프의 minimal building block을 이해하면 DAG에서 발생하는 flow에 대해 이해할 수 있습니다. Minimal building block은 크게 3가지입니다.

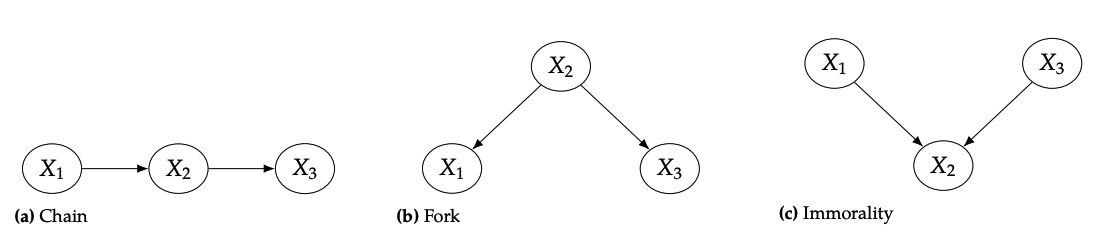
그림의 (a) Chain과 (b) fork는 동일한 set of dependencies를 가지고 있습니다. 둘 모두 $X_1$과 $X_2$가 dependent하고 $X_2$와 $X_3$가 dependent합니다.

그렇다면 $X_1$과 $X_3$는 어떨까요? 두 케이스 (a), (b) 모두 dependent합니다. 즉 association이 $X_2$로 인해 flow한다고 볼 수 있습니다. (a)의 경우는 직관적입니다. $X_1$이 $X_2$에 영향을 주고, $X_2$가 $X_3$에 영향을 주기 때문에 $X_1$과 $X_3$가 dependent함을 알 수 있습니다. (b)에서는, 두 노드의 공통 노드인 $X_2$의 값을 $X_1$과 $X_3$에 모두 영향을 주기 때문입니다. 즉 $X_1$과 $X_3$가 common cause를 갖고 있기 때문입니다.

또한 (a)와 (b)는 동일한 set of independencies를 갖고 있습니다. 만약 $X_2$을 condition으로 걸어주면 두 경우 모두 $X_1$과 $X_3$의 the flow of association이 막혀버립니다(ㅠ(block). 이 경우는 local Markov assumption 때문입니다.

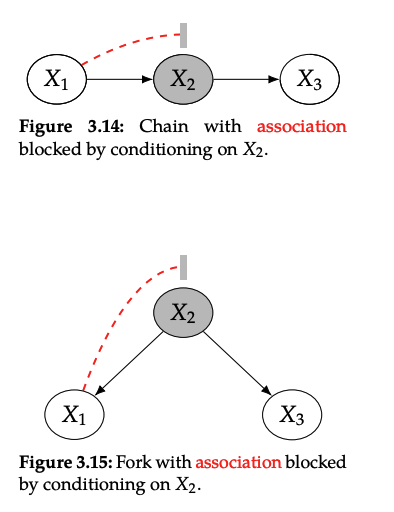
3.6 Coliders and their Descendants

Immorality($X_1$→ $X_2$ ← $X_3$)에서 $X_1$, $X_3$는 chain과 fork와는 다르게 독립입니다. 이 때 common child($X_2$)는 보통 collider라고 불립니다. 여기서는 특이하게 collider를 condition으로 걸어주는 순간, 두 변수 $X_1$, $X_3$가 종속이 됩니다. 이것을 이해하기 위해 한 가지 예시를 살펴봅시다.

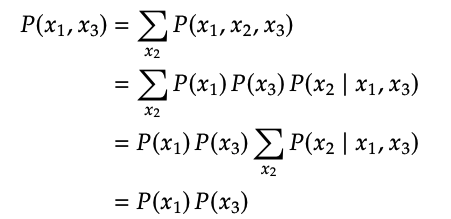
Good-Looking Men are Jerks
$X_1$: "looks", $X_2$: "availability", $X_3$: "kindness"

그림(c)의 상황은 Berkson’s paradox라고도 불립니다.

3.7 d-separation

d-separation을 정의하기 전에, "blocked path"라는 것을 다시 한 번 살펴보자면 다음과 같습니다.

Definition 3.3 (blocked path) A path between nodes $X$ and $Y$ is blocked by a (potentially empty) conditioning set $Z$ if either of the following is true:
1. Along the path, there is a chain · · · → $W$ → · · · or a fork · · · ← $W$ → · · ·, where $W$ is conditioned on ($W$ ∈ $Z$).
2. There is a collider $W$ on the path that is not conditioned on ($W$ ∉ $Z$) and none of its descendants are conditioned on (de($W$) $\nsubseteq$ $Z$).

unblocked path는 단순히 not blocked path입니다.

Definition 3.4 (d-separation) Two (sets of) nodes $X$ and $Y$ are d-separated by a set of nodes $Z$ if all of the paths between (any node in) $X$ and (any node in) $Y$ are blocked by $Z$.

만약 어떤 두 노드 $X$와 $Y$ 사이의 모든 path가 막혔다면(block), $X$와 $Y$가 d-separated 되었다고 합니다. 비슷하게, 만약 어떤 두 노드 $X$와 $Y$ 사이에 block되지 않은 적어도 하나의 path가 존재한다면, $X$와 $Y$가 d-connected 되었다고 합니다.

d-separation을 conditional independence로도 볼 수 있는데, 이 때 다음과 같은 notation을 사용합니다.

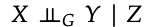
즉, $X$와 $Y$가 그래프 $G$에서 $Z$를 conditioning 해줬을 때 d-separated 되어있다.

3.8 Flow of Association and Causation

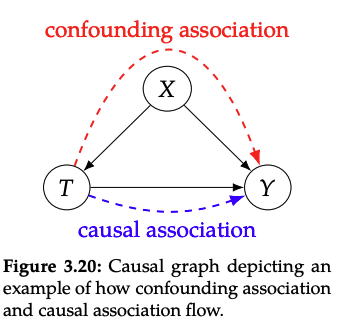
directed path를 따르는 flow association이 causal association입니다. 인과관계가 아닌 association을 만드는 대표적인 non-causal association에는 confounding association이 있습니다.