ML basic

딥러닝의 기본 요소

Data = 이미지 등에 학습 모델에 필요한 자료
model = 데이터가 주어졌을 때 이를 학습하고자 하는 것 ex) AlexNet, LSTM 등
loss = 모델을 어떻게 학습할지, 잘 학습했는지 판단하는 목표 지표 ex) MSE, CE, MLE 등
algorithm = loss function을 최소화 시키고자 하는 것

Historical Review

2012 : AlexNet
2013 : DQN
2014 : Encoder/Decoder, Adam
2015 : GAN, ResNet
2017 : Transformer
2018 : fine-tuned NLP models
2019 : GPT-3
2020 : Self-Supervised Learning (SimCLR)

MLP (Multi-Layer Perceptron)

선형 회귀 모델

• data : $\mathcal{D}=\left\{\left(x_{i}, y_{i}\right)\right\}_{i=1}^{N}$
• Model : $\hat{y}=w x+b$
• loss : $\frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2}$

loss를 줄이기 위해 w,b에 각각 loss를 편미분 한 값을 뺀다.

• $\frac{\partial \operatorname{loss}}{\partial w}$ = $-\frac{1}{N} \sum_{i=1}^{N}-2\left(y_{i}-w x_{i}-b\right) x_{i}$
• $\frac{\partial \operatorname{loss}}{\partial w}$ = $-\frac{1}{N} \sum_{i=1}^{N}-2\left(y_{i}-w x_{i}-b\right) x_{i}$

딥러닝은 결국 Neural Networks을 여러개를 쌓는 것을 뜻한다.
하지만, 여러개의 network를 쌓는 것은 한 단자의 Neural Network와 다를 것이 없다.
단순히 선형 결합

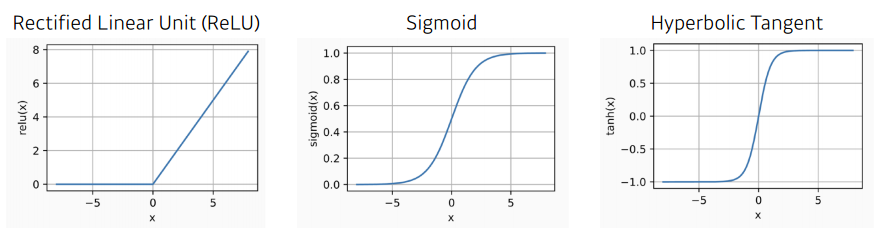
• 활성 함수

$w \leftarrow w-\eta \frac{\partial \operatorname{loss}}{\partial w}$
$b \leftarrow b-\eta \frac{\partial \operatorname{loss}}{\partial b}$
$\eta$ 은 학습률

단순히 선형 결합을 반복하는 것이 아닌, 활성 함수를 거치고 선형 결합을 하여야 한다.

• 활성 함수
  

MLP(multi-layer perceptrons)

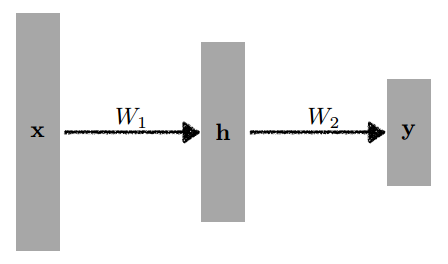
한 단 이상의 hidden vector가 있는 것을 MLP(multi-layer perceptrons)이라고 한다.

loss function은 주로 MSE (회귀) , CE (분류), MLE (추정) 등을 사용한다.

• Mean Squared Error
  $\mathrm{MSE}=\frac{1}{N} \sum_{i=1}^{N} \sum_{d=1}^{D}(y_{i}^{(d)}-\hat{y}_{i}^{(d)})^{2}$
• cross entropy
  $\mathrm{CE}=-\frac{1}{N} \sum_{i=1}^{N} \sum_{d=1}^{D} y_{i}^{(d)} \log \hat{y}_{i}^{(d)}$
• Maximum Likelihood Estimation
  $\mathrm{MLE}=\frac{1}{N} \sum_{i=1}^{N} \sum_{d=1}^{D} \log \mathcal{N}\left(y_{i}^{(d)} ; \hat{y}_{i}^{(d)}, 1\right)$

Data visualization

데이터 시각화란 데이터를 그래픽 요소로 매핑하여 시각적으로 표현하는 것

정답은 없지만, 지금까지 연구되고 사용된 시각화 모범 사례를 통해 좋은 시각화를 만들 수 있다

시각화의 요소

데이터셋의 종류

• 정형 데이터
  • 일반적으로 csv, tsv 파일로 제공된다.
  • Row = 데이터 한개, Column = attribute
• 시계열 데이터
  • 시간, 흐름에 따른 데이터
  • 기온, 주가 (정형 데이터) + 음성 비디오(비정형 데이터)
  • 추세, 계절성, 주기성을 살핀다.
• 지리 데이터
  • 지도 정보 및, 보고자 하는 정보간의 조화가 중요하다, 지도 정보를 단순화시키는 경우도 있다.
• 관계형(네트워크) 데이터
  • 객체와 객체 간의 관계
  • 객체는 Node, 관계는 Link, mapping 방법이 중요하다.
• 계층적 데이터
  • 회사 조직도, 가계도 등
  • 네트워크 시각화로도 표현 가능
• 비정형 데이터

데이터의 종류

데이터의 종류는 4가지로 분류된다.

• 수치형
  • 연속형(길이, 무게), 이산형(사람수, 주사의 눈금)
• 범주형
  • 범주형(혈액형, 종교), 순서형(학년, 등급)

시각화 이해하기

mark = 점, 선, 면으로 이루어진 데이터 시각화
channel = 각 마크를 변경할 수 있는 요소(색상, 모양, 크기등)

전주의적 속성 = 주의를 주지 않아도 인지하게 되는 요소

• 시각적 분리를 이용한다...(하나만 크기를 크게하기, 하나만 색깔을 다르게 하기 등)
• 동시에 사용하면 인지하기 어렵다.

matplotlib

1. plt.show() = 화면에 표시하는 기능을 한다. Jupyter을 사용할 때는 자동으로 표시되기 때문에 호출할 필요가 없다.
2. 
   ~.add_subplot = subplot 추가하기 plt.figure(figsize=(a, b)) = a:b 비율의 사각형을 만들기

a = plt.figure(figsize=(9, 4))
a.add_subplot(211) #2개로 세로로 쪼개서 위쪽에  
a.add_subplot(212) #2개로 세로로 쪼개서 아래쪽에    

3. color 지정은 다음과 같다.

f = plt.figure()
a = f.add_subplot(111)
a.plot([1, 1, 1]) 
a.plot([0, 0, 0], color = 'k') #1
a.plot([-1, -1, -1], color = 'black') #2
a.plot([2, 2, 2], color = '#000000') #3 hex code
plt.show()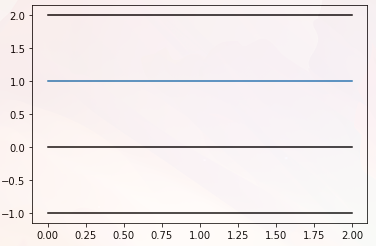

4. .legend()

f = plt.figure()
a = f.add_subplot(111)
a.plot([1, 1, 1]) 
a.plot([0, 0, 0], color = 'k', label = '1') #1
a.plot([-1, -1, -1], color = 'black', label = '2') #2
a.plot([2, 2, 2], color = '#000000', label = '3') #3
a.legend(loc= 1)
plt.show()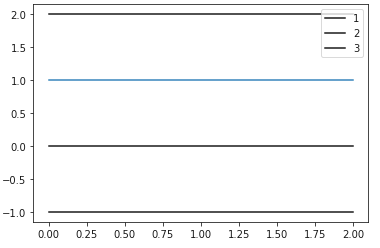

.legend() 위치 지정

함수	기능
set_title()	subplot제목 지정
suptitle()	figure 제목 지정
set_xticks([~])	x축에 적는 리스트 지정
set_xticklabels([])	x축에 적는 리스트와 맞도록 x축의 이름 지정
.text(x = a, y = b, s = '')	(a, b)위치에 s 적는 기능
.annotate	text기능 + 화살표 등 부가기능 참고

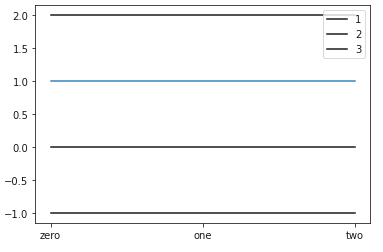
f = plt.figure() #ex) set_xticks, set_xticklabels
a = f.add_subplot(111)
a.plot([1, 1, 1]) 
a.plot([0, 0, 0], color = 'k', label = '1') #1
a.plot([-1, -1, -1], color = 'black', label = '2') #2
a.plot([2, 2, 2], color = '#000000', label = '3') #3
a.set_xticks([0, 1, 2])
a.set_xticklabels(['zero', 'one', 'two'])
a.legend(loc= 1)
plt.show()