Optimization

Generalization (일반화 성능)

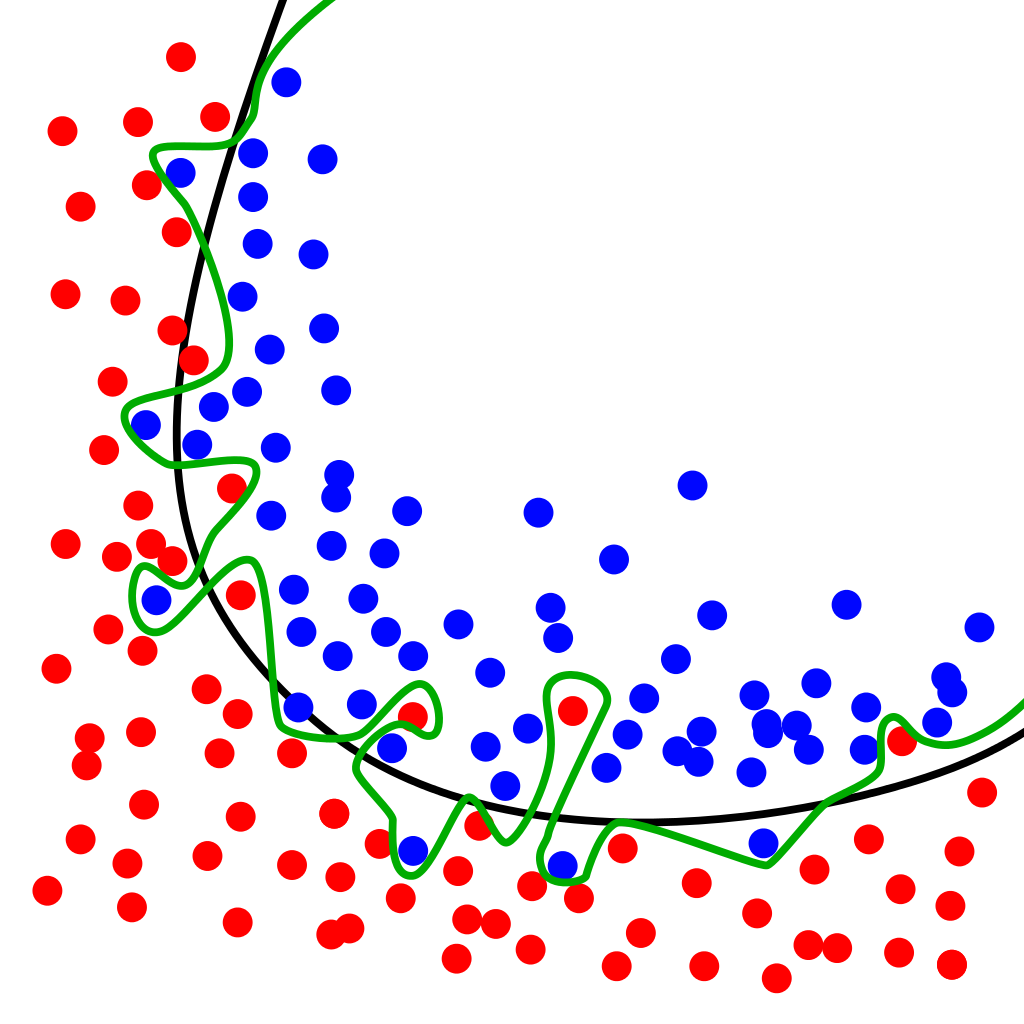
학습을 반복하면 Training error는 줄어들 수 밖에 없다. 하지만 이것은 원하는 최적값에 도달했다는 것을 보장해 주지는 않는다. 어느정도 반복을 하게 되면 test error는 오히려 커지게 된다.
이 test error와 training error의 차이를 Generalization gap이라고 한다.

초록선처럼, 학습 데이터를 과하게 학습한 것을 overfitting(과적합)이라고 한다.

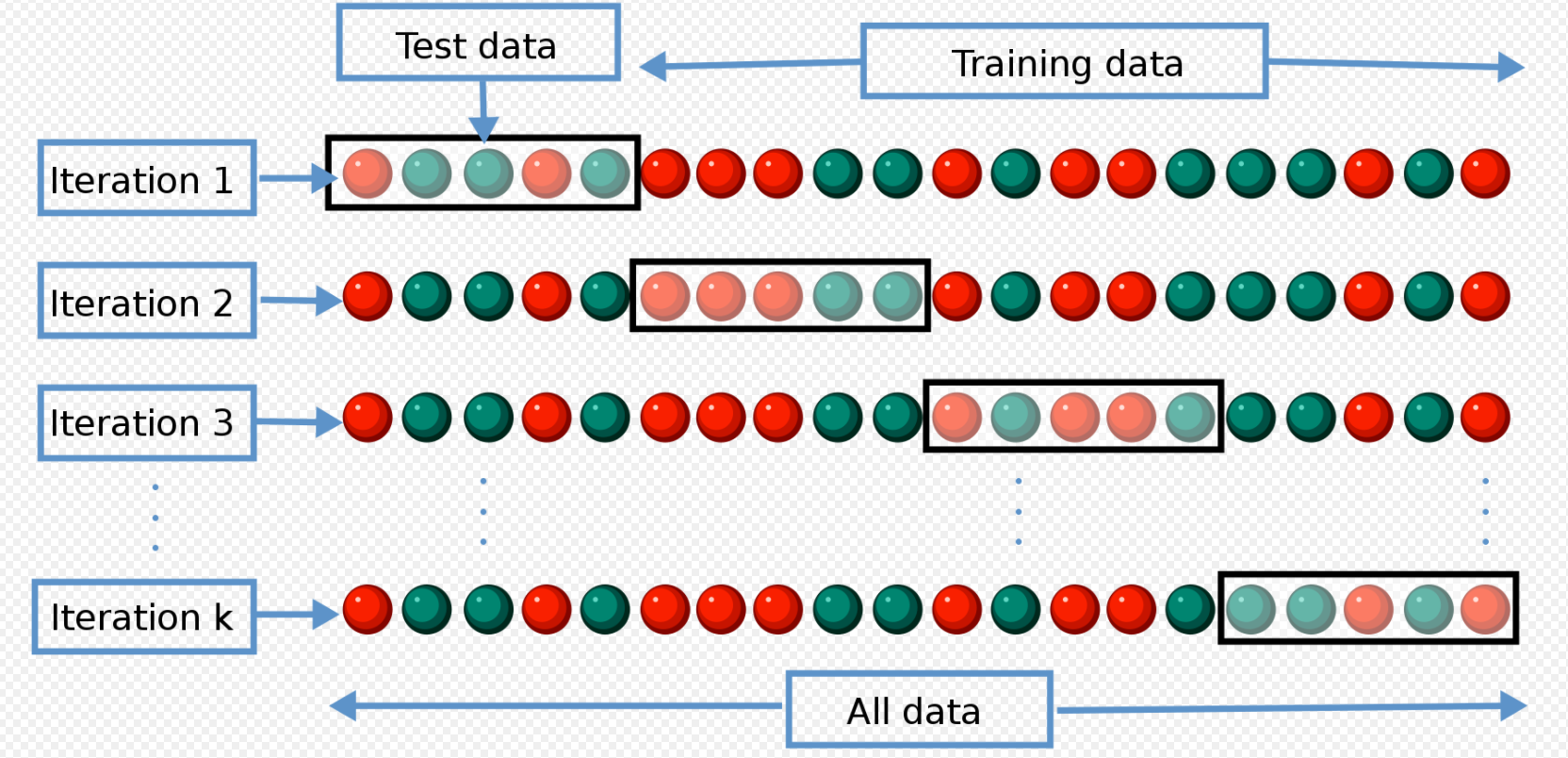
cross-validation, k-fold validation

k개로 데이터 셋을 쪼개 k-1개로 학습시킨 후 나머지 하나로 테스트를 하는 것을 cross-validation이라고 한다.

파라미터 : 내가 최적해서 찾고 싶은 값 ex) bias 등
하이퍼 파라미터: 내가 정하는 값 ex) learning rate 등

bias and Variance

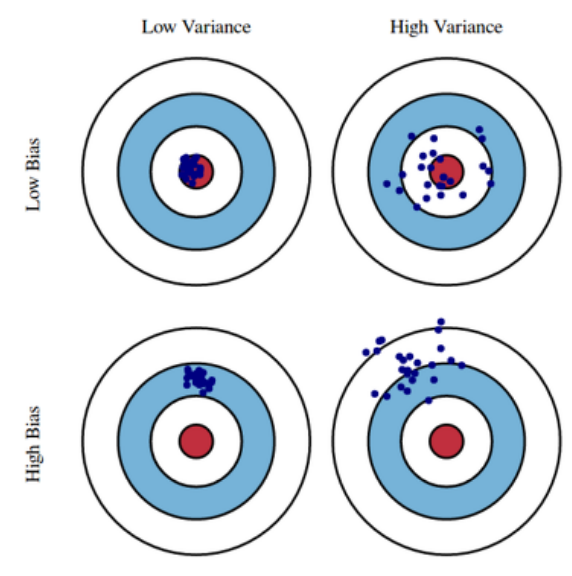
편향은 학습 알고리즘에서 잘못된 가정을 했을 때 발생하는 오차이고, 분산은 트레이닝 셋에 내재된 작은 변동(fluctuation) 때문에 발생하는 오차이다.

다음 식을 보자.

모델의 특성이 bias를 줄이면 variance가 커질 가능성이 높고, variance를 줄이면 bias가 커질 가능성이 크다. noise가 존재할 경우에, bias와 variance를 같이 줄이는 방법은 구하기 힘들다.

Bootstrapping

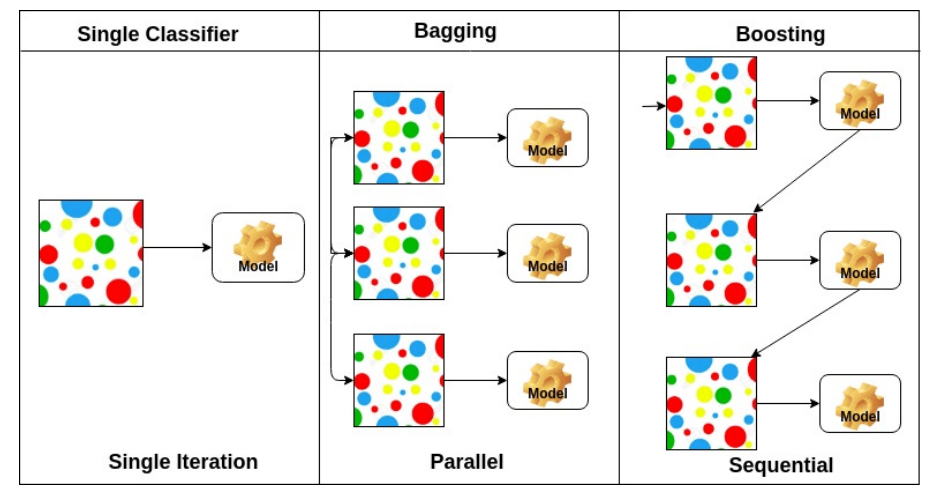
Bagging(bootstrap aggregating)
고정된 학습 데이터가 있을 때, 그 안에서 random sampling을 이용해 여러 개의 모델을 만들어, 각각의 결과가 얼마나 일치하는지 확인하는, 정확도를 확인하는 기법이다.
ex) 학습 데이터중 80%의 학습 데이터를 사용하는 n개의 모델의 결과 값을 사용하여 도출해낸 성능이 모든 학습 데이터를 사용한 1개의 모델의 성능보다 더 좋은 성능을 낼 때가 많다.

Boosting
고정된 학습 데이터가 있을 때, 모델을 만든 후 잘 분류되지 않은 데이터를 따로 취합해 이에 대한 모델을 새로 만드는 것을 반복하여 결국에는 이렇게 만들어진 모델을 모두 합치는 것.

Gradient Descent Methods

• Stochastic Gradient descent
• Mini-batch gradient descent
• Batch gradint descent

대부분의 Gradient Descent를 사용할 때는 Mini-batch gradient descent를 사용한다.

• Batch-size
  큰 배치 사이즈를 사용하는 것보다는 sharp minimizers가 일어나게 되고, 배치 사이즈를 사용하는 것은 flat minimizer가 일어나는데, 배치 사이즈를 작게 사용하는 것이 일반적으로 성능이 더 좋다. 일반적으로 Generalization가 좋아지기 때문이다.
  
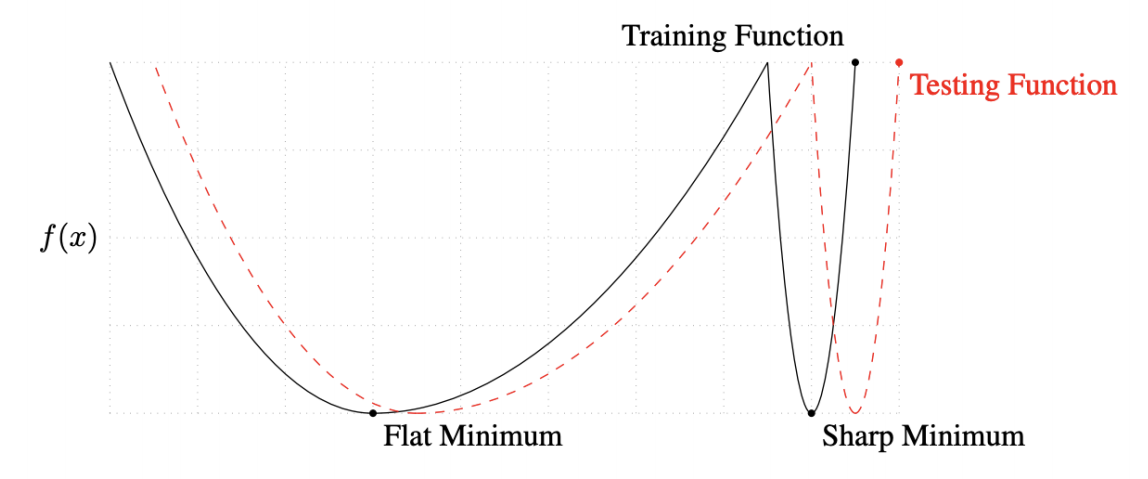
• flat minimum = training function에서 잘 되면, testing Function에서 잘 동작하는 것, 즉, 일반화 성능이 좋다.
• sharp minimizers = training function에서 잘 되어도, testing Function에서 잘 동작하지 않을 수 있다.

Optimizer

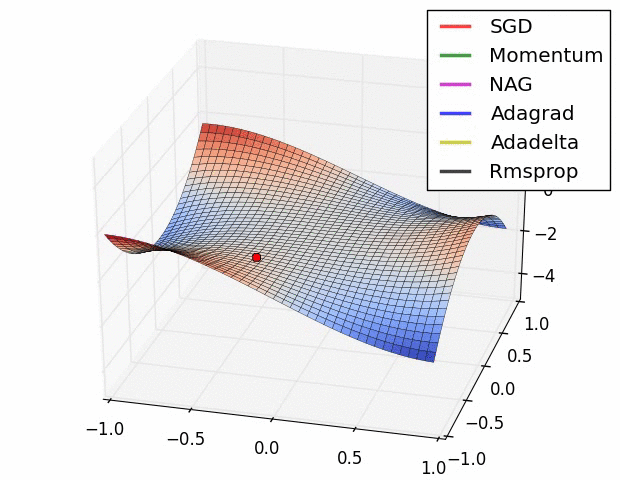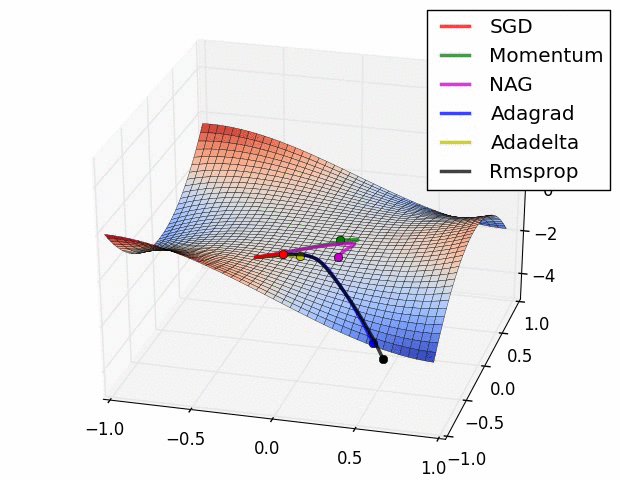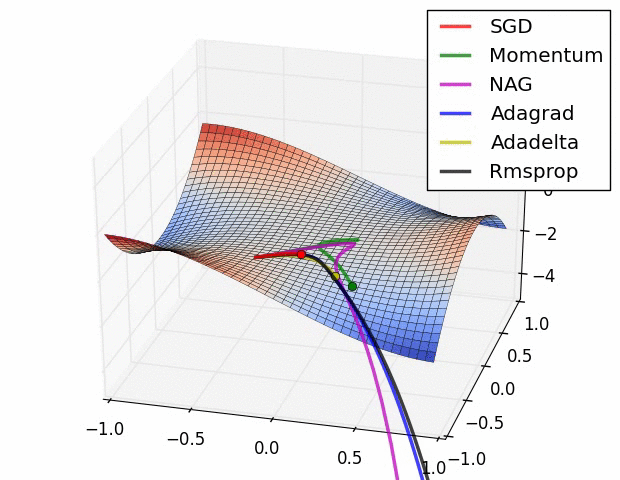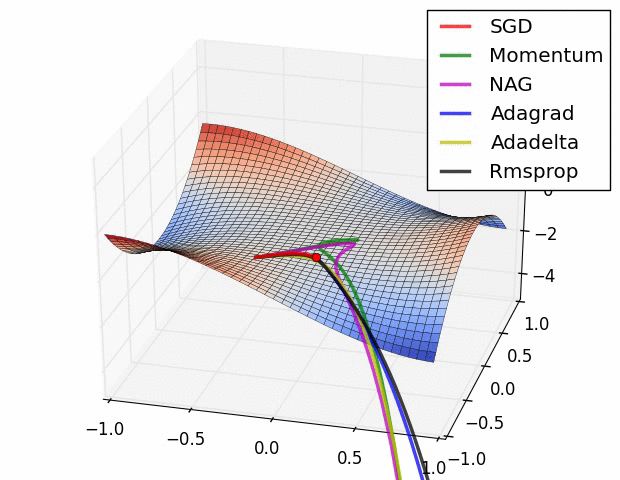
• 기본적인 Gradient descent
  $W_{t+1} \leftarrow W_{t}-\eta \underset{gradient}{g_{t}}$

이는 Learning rate를 조절하는 것이 어렵다. 너무 크면 학습이 안되고, 너무 작으면 학습을 아무리 시켜도 학습이 되지 않는다.
이를 발전시키고자, gradient 값만 사용해도 더 좋은 성능을 낼수 있도록 optimizer가 등장한다.

Momentum

$\beta$(momentum)이라는 하이퍼 파라미터가 들어간다.
하이퍼 파라미터 momentum과 gradient를 합친 $a_{t+1}$(accumulation)를 이용한다.
한번 흘러가게 된 gradient 방향을 어느정도 유지시키기 때문에 gradient 값이 변동이 심해도 어느 정도 유지시켜주는 장점이 있다.

NAG(Nesterov Accelerated Gradient)

Lookagead gradient = a라고 하는 현재 정보가 존재하면 그 방향으로 그레디언트를 계산한 것을 이용해 accumulation을 만든다.

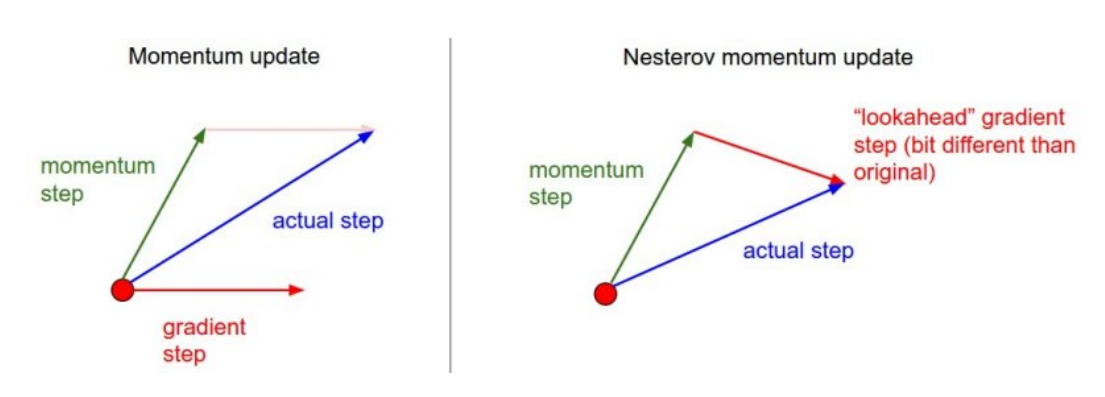
Momentum의 local minima로 도달하는데 매우 오래걸릴 수 있는 문제를 보완할 수 있다.

Adagrad

지금까지 많이 변화한 파라미터는 적게 변화시키고, 적게 변한 파라미터는 많이 변화시키기 위해 각 파라미터가 얼만큼 변화했는지 알려주는 $G_t$를 이용한다.
$\epsilon$ = 분모가 0이 되지 않게 하기 위한 값

가장 큰 문제는 $G_t$는 계속해서 커지기 때문에, 결국 무한대로 가게되면 학습이 멈춰지는 현상이 생긴다.

Adadelta

$G_t$의 지속적인 증가를 최대한 줄이겠다는 목적으로 t에 대한 window size만큼의 파라미터만 얼만큼 변화했는지 확인한다.

window size만큼의 $G_t$를 가지고 있어야 해서 window size가 커지면 파라미터의 갯수의 부담이 커지기 때문에 이를 방지하기 위해 exponential moving average를 이용한다.

learning rate가 없기 떄문에 바꿀수 있는 요소가 많지 않아 잘 사용되지 않는다.
learning rate가 없어도 $H_{t}$(EMA of difference squares)가 W의 변화값을 가지고 있어, 어느정도 학습을 할 수 있다.

RMSprop

Adagrad에서 사용되었던 $G_t$에 exponential moving average를 이용한다.

Adam(Adaptive Moment Estimation)

RMSprop에 사용되었던 각 파라미터의 변화량과 momentum을 같이 활용한다. 무난하게 많이 쓰이는 Optimizer이다.
$m_t$ = Momentum
$v_t$ = EMA of gradient squares

• 하이퍼 파라미터
  $\beta_{1}$ = m_t를 얼마나 유지시킬지 결정하는 변수
  $\beta_2$ = v_t를 얼마나 유지시킬지 결정하는 변수
  $\eta$ = learning late
  $\epsilon$ = 분모가 0이 되지 않게 하기 위한 값

$\epsilon$의 값을 조절하는 것이 매우 중요하다.

Regularization

학습을 방해함으로, 얻는 이점은 test data에도 잘 동작하게 하도록 한다.

• Early stopping
  말 그대로 Generalization gap가 작을 때 멈추는 방법

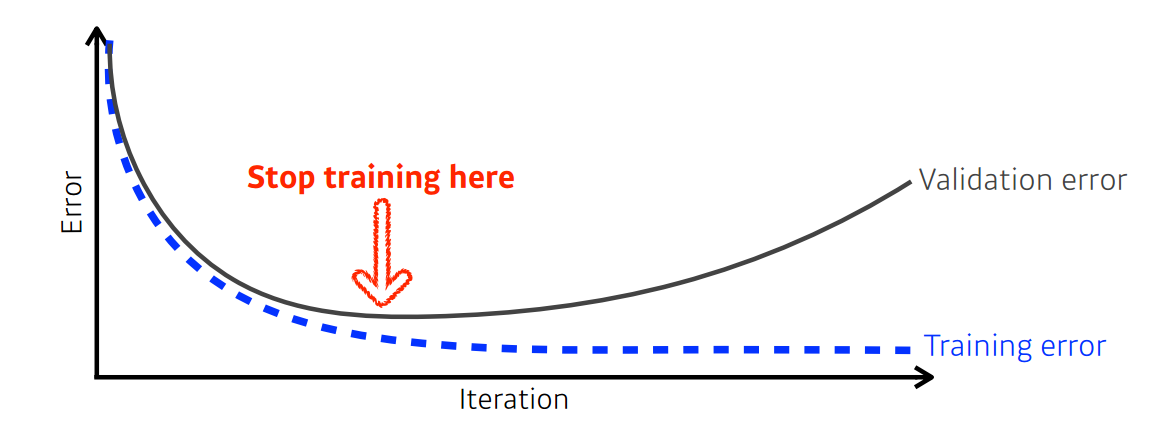
• Parameter norm penalty

neural network 파라미터가 너무 커지지 않게 하기 위해 이 방법을 사용한다.

• Data Augmentation

주어진 데이터를 변형하는 방법
ex) 이미지 90도 회전 등

Data Augmentation은 데이터에 따라 주의하여야 한다. ex) NMIST 숫자 6 뒤집기 -> 9

• Noise Robustness

입력 데이터에 노이즈를 삽입하기

• Label Smoothing

학습 데이터 두개를 뽑아, 이 두개를 섞는 것

Mixup, CutMix 등은 구현이 쉽고 노력 대비 성능이 향상된 결과를 얻을 수 있다.

• Dropout

neural network 일부의 weigth를 0으로 만든다.

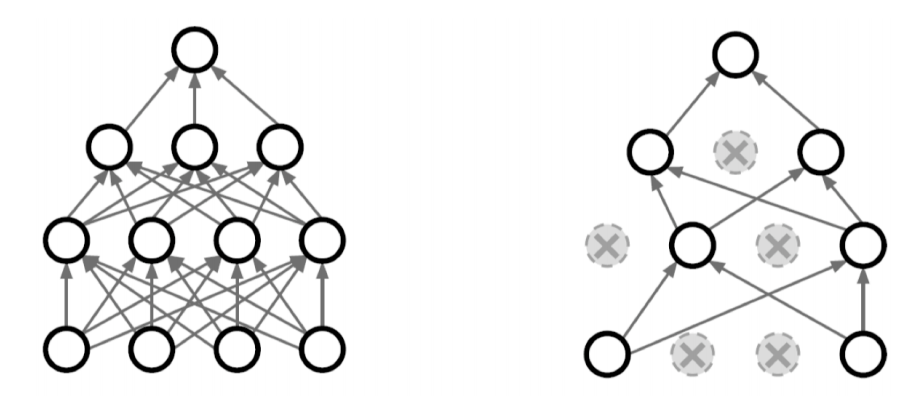
• Batch Normalization

내가 적용시키고자 하는 layer의 Statistics를 정규화 시키는 것

일반적으로 깊은 layer가 쌓인 경우에 Batch Normalization를 사용하면 성능이 향상된다.

[참고]
https://ko.wikipedia.org/wiki/%EA%B5%90%EC%B0%A8%ED%83%80%EB%8B%B9%EB%8F%84
https://ko.wikipedia.org/wiki/%ED%8E%B8%ED%96%A5-%EB%B6%84%EC%82%B0_%ED%8A%B8%EB%A0%88%EC%9D%B4%EB%93%9C%EC%98%A4%ED%94%84
https://imgur.com/NKsFHJba