Generative Model

Generative Model의 기능

• Generation : train data에 있는 것이 아닌 이미지를 만들어내는 것
• Density estimation : 이미지가 들어왔을 때 이 이미지가 무엇인지, 확률값을 제시하는 모델, 이를 explicit models이라고 한다.
• Unsupervised representation learning : 이미지의 특징을 학습한다. ex) ears, tail, etc 등

p(x)를 만드는 방법

위 사진과 같은 X_1,...,X_n과 같은 n개의 binary pixel이 있다고 가정해보자.
가능한 possible states

필요한파라미터 수

매우 많은 파라미터 수가 필요하다. 기계학습은 파라미터 수가 많을 수록 학습이 어렵기 때문에 파라미터 수를 줄이는 방법이 필요하다.

만약 n개의 픽셀이 independent한다면($p(x_1,...,x_n) = p(x_1)p(x_2)...p(x_n)$)
가능한 possible states는 $2^n$이다. 하지만 필요한 파라미터의 개수는 n개이다.

필요한 파라미터 수가 $2^n$개에서 n개로 줄어들었다! indenpence assumption이 얼마나 강한 모델인지 보여준다.

이를 종합하면
fully dependence = 너무 많은 파라미터가 필요함
independence = 파라미터는 크게 줄지만, 표현할 수 있는 이미지가 사실 너무 적다.

따라서 이 둘의 타협점을 찾아야 한다. 그것을 찾기위해 여러가지 방법을 사용한다.
chain rule = $p(x_1,...,x_n) = p(x_1)p(x_2|x_1)...p(x_n|x_1,...,x_{n-1})$
Bayes'rule = $p(x|y) = \frac{p(x, y)}{p(y)} = \frac{p(y|x)p(x)}{p(y)}$
conditional independence = if $x \bot y|z$, $p(x|y, z) = p(x|z)$
z라는 random variable이 주어졌을 때, x와 y는 independent하기 때문에 x라는 random variable을 표현하는데 있어 z가 주어지면 y는 상관이 없다.

• chain rule을 사용시 필요한 파라미터 수

  • $p(x_1)$ = 1개의 파라미터(0또는 1)
  • $p(x_2|x_1)$ = 2개의 파라미터 ($p(x_2|x_1)$ 이 0또는 1일때)
  • $p(x_3|x_1,x_2)$ = 4개의 파라미터
    $1 + 2 + 2^2 + 2^3 + \dotsb + 2^{n-1} = 2^n - 1$

• Markov assumption

  $X_{i+1} \bot X_1,...,X_{i-1}|X_i$

  예를 들어, $X_10$은 $X_9$와 dependent하고, 나머지 요소들과는 independent하다는 것을 뜻한다.
  이를 나타내면
  $p(x_1,...,x_n) = p(x_1)p(x_2|x_1),p(x_3|x_2)...p(x_n|x_{n-1})$과 같고, 필요한 파라미터 수는 2n - 1로 크게 줄어든다.

이를 Auto-regressive models이라 부르고 conditional independence를 잘 활용하는 것이 특징이다.

Auto-regressive models

• NADE (Neural Autoregressive Density Estimator)
  

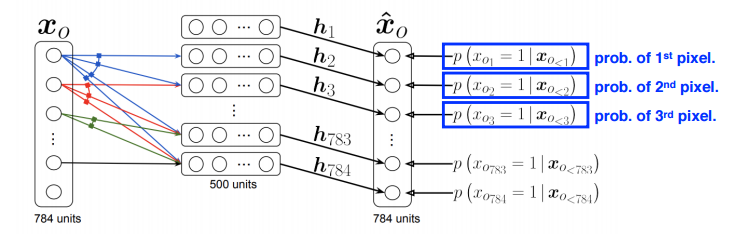
i번째 pixel의 확률을 첫번째 pixel 부터 i-1번째 pixel에 dependent하게 하는 것

$p(x_i|x_{1:i-1}) = \sigma(a_ih_i + b_i)$
$h_i = \sigma(W_{<i}x_{1:i-1} + c)$
neural network 입장에서는 입력 차원이 계속 바뀐다. 첫번째 pixel을 어느 것과도 dependent하지 않게 만들고, 두번째 pixel부터 1개의 입력(첫 pixel), n번째 pixel은 n-1개의 입력을 받기 때문이다.

NADE는 explicit 모델로, 임의의 binary vector가 주어지면 확률을 계산할 수 있다.
joint probability를 이용해 각각을 independent하게 바꾼다.

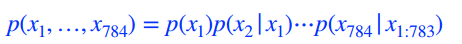
만약 decrete가 아닌 continuous random variable output이 필요할 땐 sigmoid가 아닌 마지막 layer에 a mixture of gaussian을 활용한다.

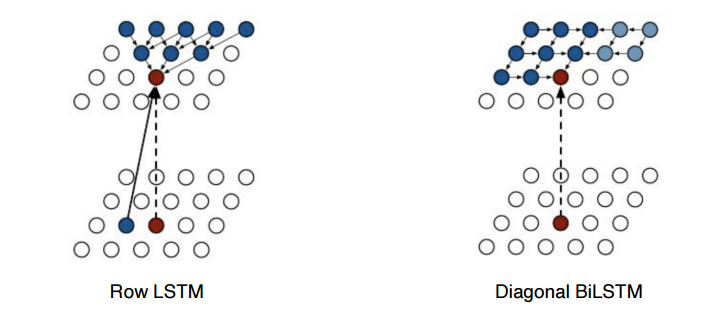
• Pixel RNN
  
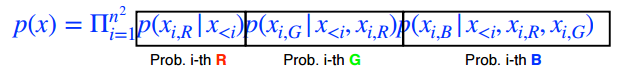
  이미지의 pixel을 만들어내고 싶어하는 Generative Model

RNN을 통해 generation을 하는 것
Row LSTM이나 Diagonal BiLSTM 알고리즘을 사용한다.

Latent Variable Models

Variational Auto-encoder

Variational inference의 목적 : posterior distribution을 찾는 것

Variational distribution : 일반적으로 Posterior distribution을 계산하기는 매우 힘들다. 그래서, 내가 최적할 수 있는 값으로 근사하는 것
즉, posterior distribution을 최대한 잘 근사할 수 있도록 하는 variational distribution이 중요하다.

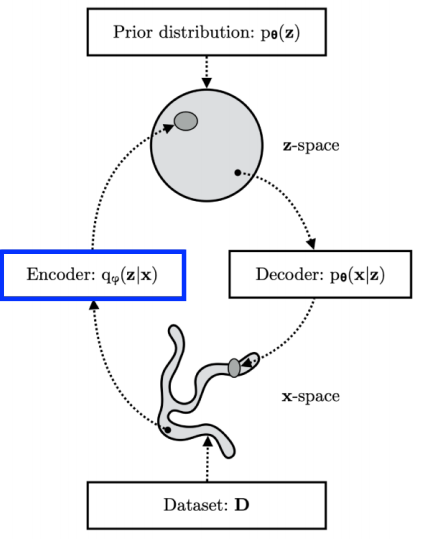
내가 관심있어하는 posterior distribution 근사하고자 encoder를 사용한다.
posterior 값을 모르는데 찾는 것을 ELBO(Evidence lower bound)라고 한다.

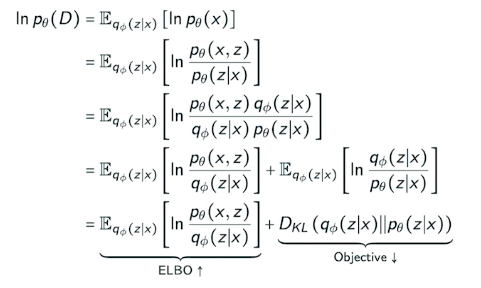
이 수식은 궁극적으로, Evidence lower bound라는 것을 계산해 증폭시킴으로써, objective의 값을 줄이는 것이다.
KL Divergence = 두 확률 분포의 다름의 정도
이를 활용해서 Variational Auto-encoder를 학습하는 것이 매우 중요하다.

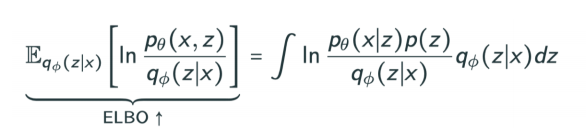
Evidence lower bound을 전개해보면, Reconstruction Term과 prior Fitting Term으로 나뉜다.
Reconstruction Term = 인코더를 통해 latent space로 보냈다가, 다시 디코더로 돌아오는 Reconstruction loss를 줄이는 것
prior Fitting Term = x라는 이미지를 잔뜩 latent space로 보내, 이것들이 이루는 분포와 prior distribution과 유사한 모양을 띄도록 하는 것

variational Auto-encoder의 key limitation:

• intractable한 model
• Gaussian 함수를 사용한다.(KL Divergence 때문에)
• isotropic Gaussian을 많이 쓴다.
  

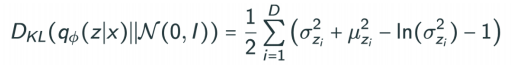
Adversarial Auto-encoder

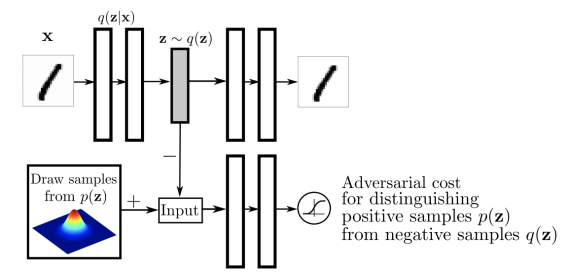
Variational Auto-encoder의 가장 큰 단점은, encoder를 활용할 때 prior Fitting Term이 KL Divergence를 활용한다. 그렇기 때문에 가우시안이 아닌 경우에는 활용하기 힘들다.

Adversarial Auto-encoder는 Variational Auto-encoder의 prior Fitting Term을 GAN objective로 변환한 것이다.

GAN(Generative Adversarial Network)

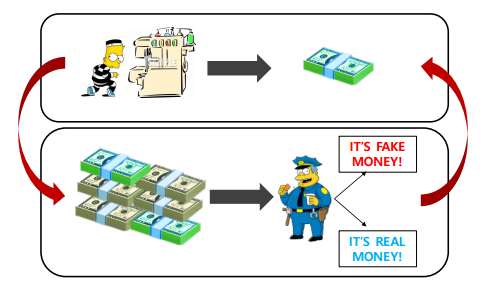
위의 사진을 보면, 위조지폐를 경찰이 분별하고, 이를 바탕으로 도둑은 경찰을 속이기 위해 더욱 치밀한 위조지폐를 만드는 것과 같이 GAN은 성능 향상을 목적으로 Discriminator는 더 잘 구별하고, Generator는 더 잘 속일수 있도록 Fake data를 만드는 것을 반복한다.
GAN의 장점은 Discriminator과 Generator를 통해 성능이 상승하고, Generator 또한 Discriminator를 통해 성능이 상승해 굉장히 좋은 이미지를 만들 수 있다.

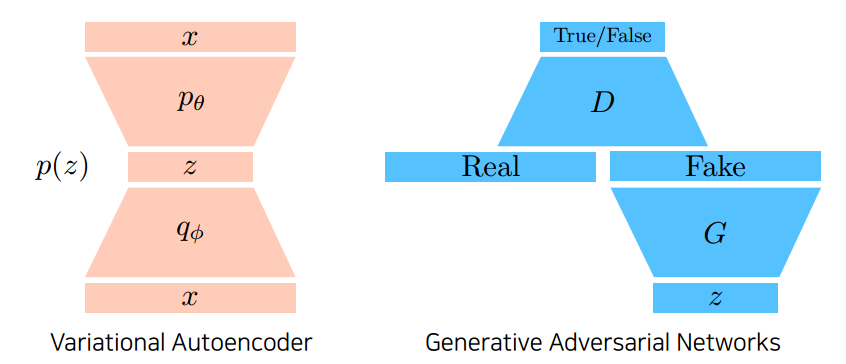
VAE와 달리 GAN은 z라는 Latent distribution 속에서 Generator를 통해 Fake를 만들고, Discriminator는 Real인지 Fake인지 구별하는 분류기를 학습을 하는 것을 반복하는 모델이다.

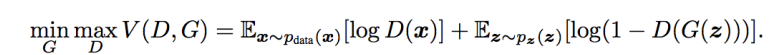
GAN은 결국 Generator와 Discriminator가 싸우는 objective를 가지고 있다고 볼 수 있다.
Discriminator의 식은 다음과 같다.

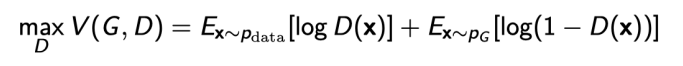
이 식을 항상 최적화 시키는 식을 optimal discriminator이라고 한다.

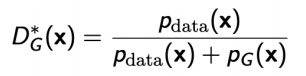
generator의 값이 고정되어있다면, 이 식에 따라 True와 False가 판별된다.

optimal discriminator를 Generator 식에 대입하면, jenson-shannon Divergence(JSD)를 얻을 수 있다.

이 식의 의미는 optimal discriminator을 대입함에 따라 generator를 통해 실제로 만들어진 True 값을 띈 데이터와 generatord에서 실제로 학습한 데이터 사이의 JSD를 최소화 시킨 것이다.

DCGAN

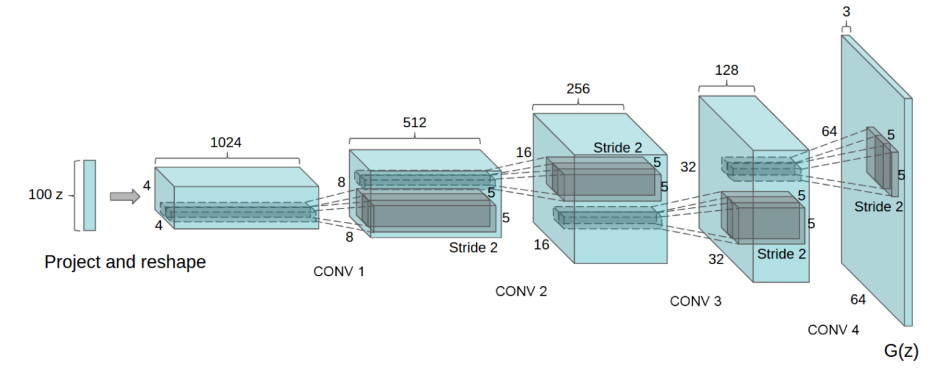
Dense layer로 이루어진 일반적인 GAN과 달리 deep convolution을 활용했다.

Text2Image

문장을 입력하면 이미지가 나온다!