머신러닝 모델의 해석 가능성에 대해 공부하고 있다.
내가 보려고 큰 흐름만 정리해둔다.
이후에 디테일한 내용과 예시코드 등을 추가할 예정이다.1. Partial Dependence Plot
1) Background
먼저 Marginal distribution(주변 분포)와 Marginalizing에 대해 알고 넘어가야 한다.
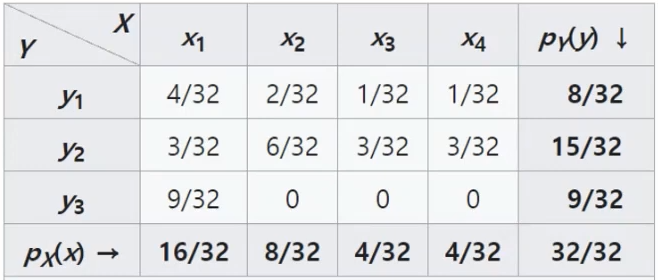
- 표 안의 확률값은 joint distribution(결합 분포)를 나타냄
- 표 양 끝(5행, 6열)이 marginal distribution을 나타냄
- 이 표는 x와 y의 수준 변화에 따른 확률값의 변화를 보여줌
- Marginalizing은 이런 marginal distribution을 계산하는 과정이다.
예를 들어, X1의 주변분포를 구하기 위해 Y의 모든 수준에 대해 확률값을 구해서 더하게 됨.
PDP는 이 Marginalizing의 개념을 가져온다. 관심 있는 변수와 예측값 사이의 marginal effect를 계산하여 보여준다. 예를 들어, 캘리포니아 집값을 여러 변수로 예측한 경우, 아래처럼 각 변수별 영향을 확인할 수 있다.
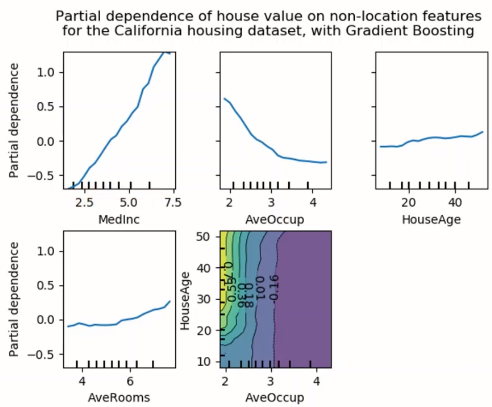
- 특정 변수의 모든 샘플에 대해 marginalizing하는 "Global method"
- 변수와 예측된 값 사이의 관계를 살펴볼 수 있음
2) Partial Dependence
📌그렇다면 partial dependence를 어떻게 구할까? 함수를 살펴보자.

- : 관심 변수
- : 관심 변수를 제외한 나머지 변수들
- : 학습이 완료된 머신러닝 모델
- : 모델과 관심변수 간의 partial function
- 적분식으로 marginalizing 해줌
위는 이론적인 수식이고, 컴퓨터에서 계산할 때는 아래와 같은 식으로 보면 된다.

-
: 나머지 변수들의 실제값 (n개 샘플에 대한 n개의 값)
-
Monte Carlo Integration
→ 는 원하는 값으로 고정해두고 ~들만 바꿔가면서 예측값 구함
→ 그리고 그걸 로 나눠서 평균 냄! = 에 대한 PD값! -
그러면, 값을 바꿔가면서 PD값 구할 수 있고, 그때의 예측값 변화 양상이 곧 PDP가 됨!
📌만약 관심변수가 범주형 변수라면?
- 이때는 다른 샘플들도 모두 동일한 범주를 갖도록 강제하여 PD값을 구함!
- ex) 계절이 '여름'일 때 어떨지 궁금하다면, 계절 column의 모든 값을 '여름'으로 바꾸고 예측값 계산 = 에 대한 PD값!

📌PDP의 관계 역시 인과관계는 아니라는 점 유의해야 함!
3) Examples
<예시1> 자전거 대여량 Regression
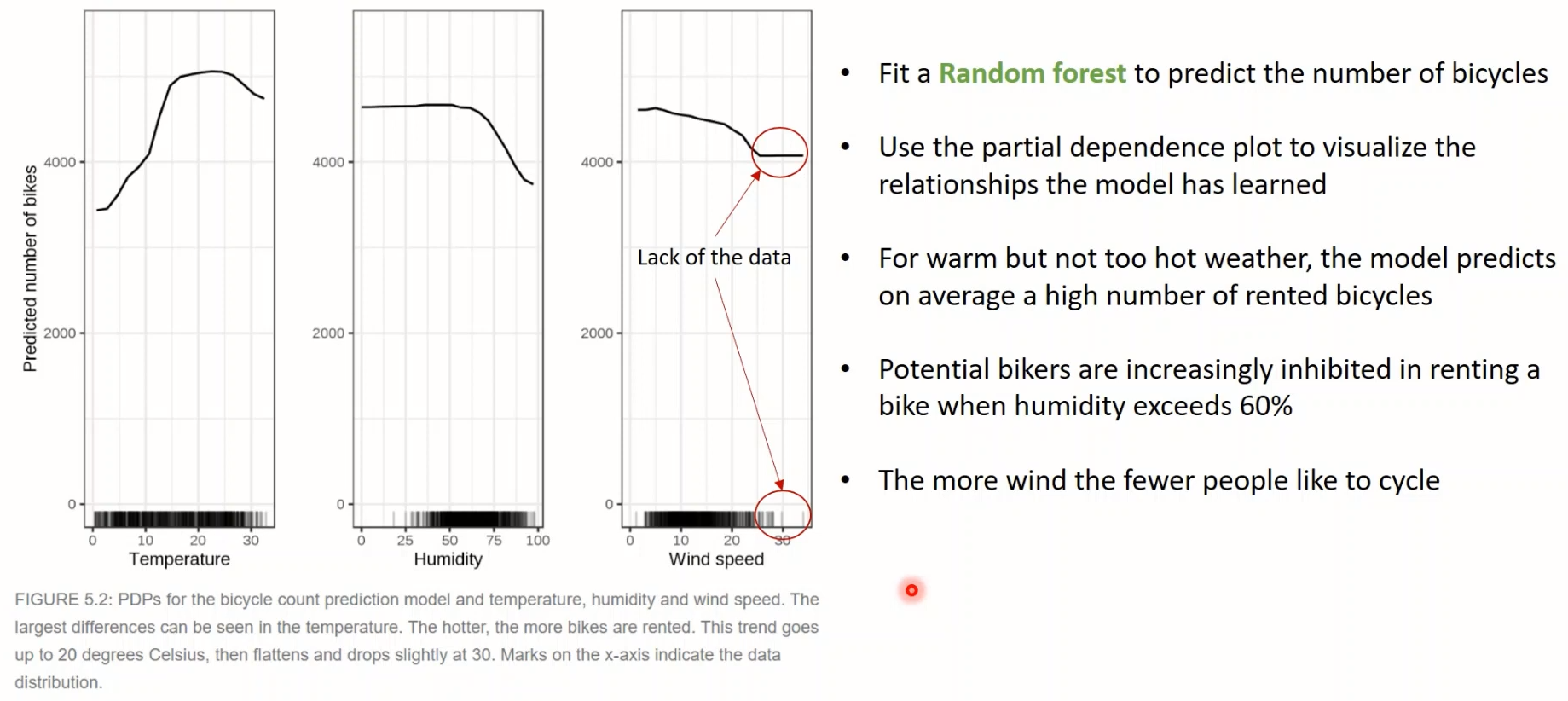
- 온도 적당할 때 제일 많이 대여함 / 습도나 풍속 너무 높으면 줄어듦
- (주의사항) 근데! X축에 나타난 데이터의 빈도를 봐야함!! 예를 들어, 풍속이 아주 높은 경우 변화가 없는 것처럼 직선으로 나타나지만, (밑에 보면) 데이터가 없어서 그런 거임

- 범주형 변수인 경우에도 막대그래프로 그려서 확인 가능함
- 봄에만 상대적으로 좀 적고, 그 외에는 계절별 영향 크지 않은 것으로 보임
<예시2> 자궁경부암 Classification
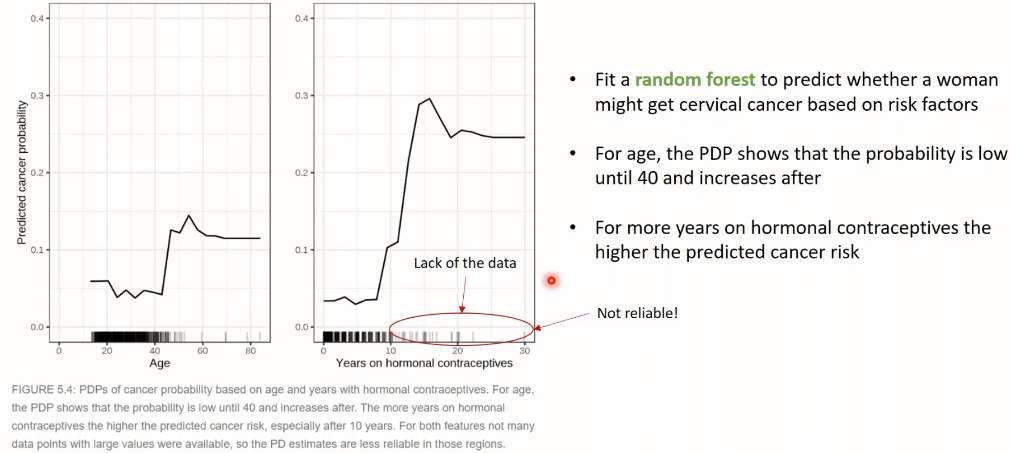
- '나이' 변화에 따른 & '호르몬피임제 사용 기간'에 따른 암 발생확률의 변화
- 수치가 큰 경우는 데이터가 부족하여 신뢰도가 높지는 않다는 점 명심
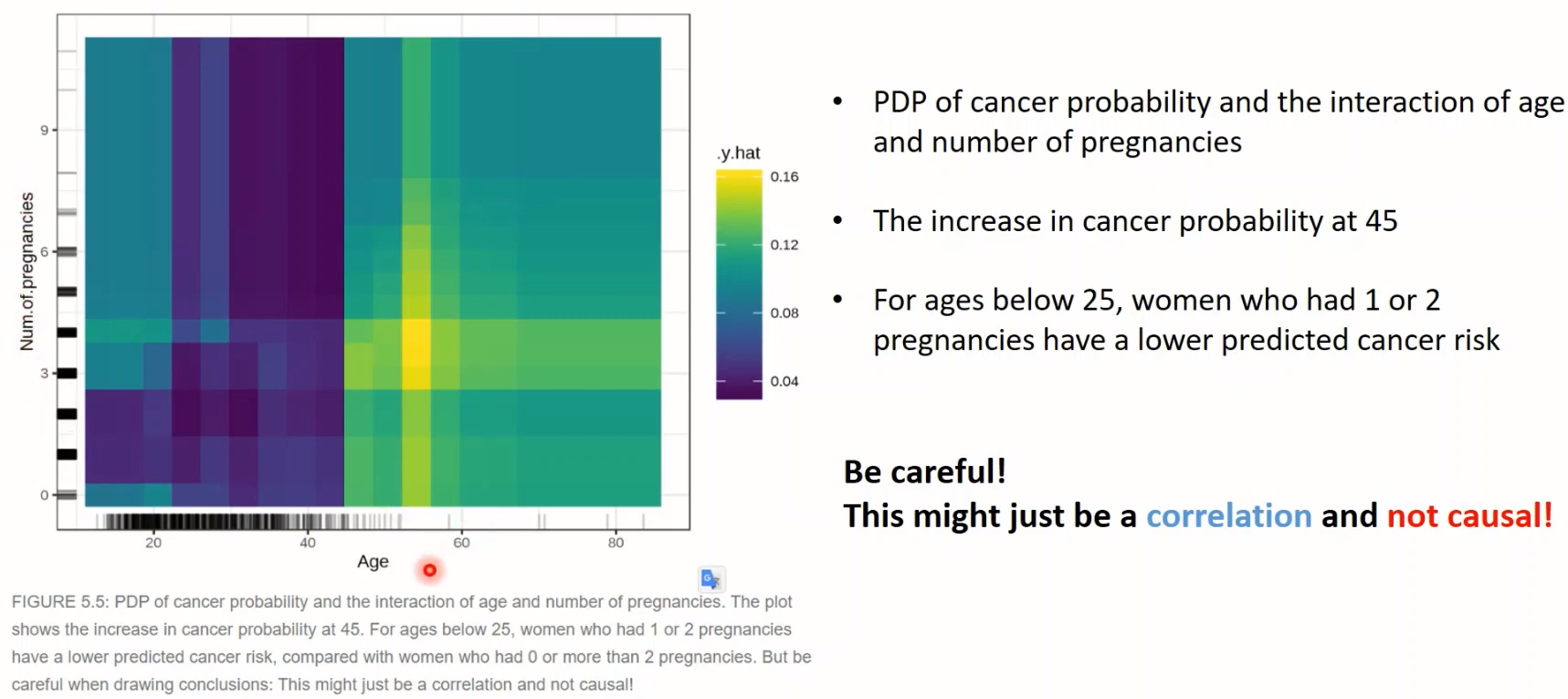
- 2개 변수를 합쳐서 plot 그릴 수도 있음!
4) Pros and Cons
<장점>
- 직관적이며 구현하기가 쉬움
- 변수간 상관이 없는 경우 해석이 용이함
- 때로는 독립변수와 예측변수가 인과관계를 고려하여 수집된 경우, 인과관계 분석으로 사용될 수 있음
<단점>
- 변수 2개까지만 시각적으로 확인할 수 있음
- 데이터가 적은 경우 신뢰성이 떨어질 수 있음 (자전거 대여량 예시 참고)
- 관심변수 가 나머지 변수 와 상관관계가 없다는 가정을 전제로 함.
if 상관이 크다면 매우 이상한 값이 나올 수 있음. - 변수간 독립성을 전제하므로 상호작용이 고려되지 않음
(ALE, ICE로 어느 정도 극복할 수 있음)
cf) 분류 문제에서도 PDP를 구할 수 있음. 클래스가 여러 개인 경우, 클래스마다의 확률에 대한 PDP를 구할 수 있음.
2. Individual Conditional Expectation curve
1) ICE plot
ICE는 PDP를 약간 수정한 개념으로 보면 된다.
- 관심 변수와 예측값의 '평균적인' 관계를 보여준 PDP와 달리, ICE는 관심 변수와 예측값의 관계를 "개별 관측치에 대해" 확인할 수 있음!
- 관측치 마다 하나의 선이 그려지는데, 이 선들의 평균을 구한 게 곧 PDP임!
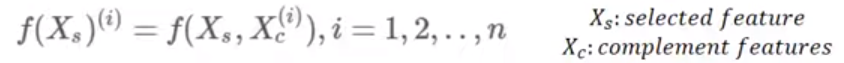
- : 관심 변수
- : 관심 변수를 제외한 나머지 변수들
- : 학습이 완료된 머신러닝 모델
- : 개별 관측치의 번호 (전체 n개 중에 i번째 관측치)
2) Examples
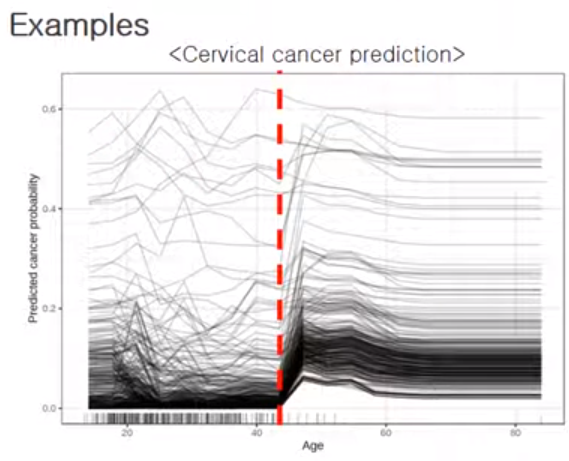
- 관심변수(ex. Age)가 가진 값마다, 함숫값을 계산해서 포인트를 찍고, 그 포인트들을 다 이으면 하나의 라인이 됨 = 1개의 ICE
- 이 작업을 개별 instance(관측치)에 대해 다 그리면 위처럼 됨!
- ICE는 개별로 보여주니까 추가적인 인사이트를 얻을 수도 있음! (2번 참고)
- e.x.)
1) 대략 45세를 기점으로 암 발생확률이 늘어나는 경향을 확인 가능!
2) 근데, 어릴 때부터 암 발생확률 높은 경우는 이후에 딱히 더 높아지지는 않음 - c.f.)
근데 또 아래 같은 경우는 ICE 그려도 전체적인 트렌드 안 따르는 샘플이 딱히 없으니, PDP만으로도 충분할 수 있음.
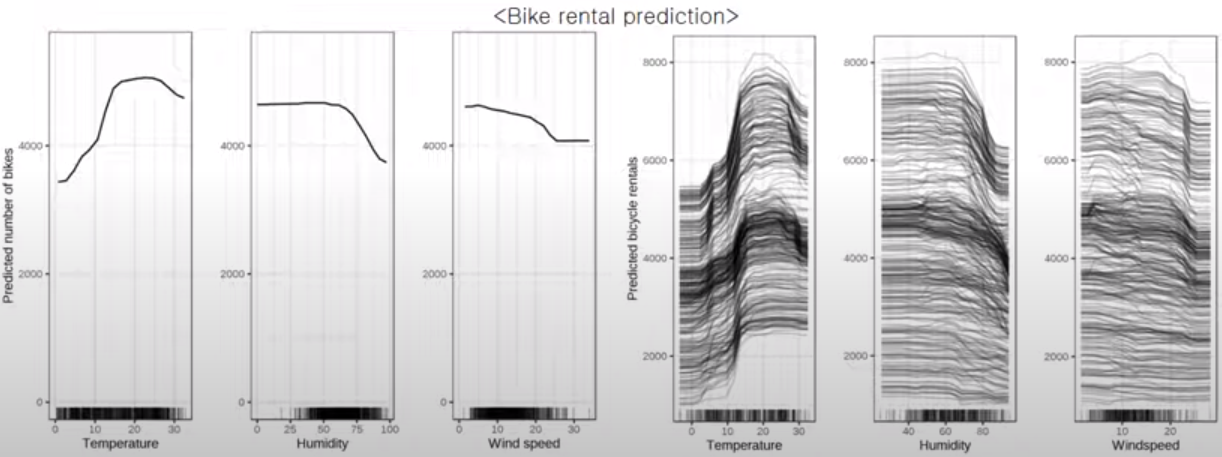
- e.x.)
3) d-ICE
ICE plot에서 개별 인스턴스의 이질성을 더 쉽게 시각화하기 위해, 각 인스턴스의 미분값을 사용할 수도 있다.(❓) 이를 derivative ICE라고 한다.

- 독립 가정이 있으니 함수를 g와 h로 분리할 수 있고, 그걸 기준으로 미분하면 미분값 이 나옴. 이 미분값으로 그래프 그리면 d-ICE 얻을 수 있음.
- 근데 계산 매우 오래 걸리는 단점 때문에 실제로는 잘 사용하지 않음.
4) Pros and Cons
<장점>
- 모든 인스턴스에 대해 확인할 수 있으니 PDP보다 이해하기 직관적임.
- 개별 인스턴스들의 이질적인 관계들을 자세히 들여다 볼 수 있다
<단점>
- 한 번에 하나의 feature만 표현 가능 (2개 피쳐도 안 됨. 면 2개가 나오니..)
- 변수 간 상관 있으면 이상한 결과 나올 수 있음. (PDP와 마찬가지)
- 모든 인스턴스를 다 그리다 보니, 인스턴스 개수 많으면 너무 복잡해져서 잘 안 보일 수 있음 ( 선 투명도 높이거나 샘플 몇 개만 뽑아서 그려보기)
- 평균적인 관계를 파악하기는 힘듦 ( PDP로 해결 가능)
참고자료
감사합니다.