문제
학생들의 점수가 배열로 주어지고 모여있는 학생끼리(문제에선 나이) 모아 조를 만드는데 조를 이룬 학생들의 점수 중 최대 점수와 최소 점수의 차이가 잘 짜여진 정도라고 정의한다. 조를 임의로 구성했을 때 잘 짜여진 정도의 합의 최대값을 구하는 문제입니다.
- 학생 수 1 <= N <= 10000
- 학생의 점수 0 <= M <= 100000
접근
전형적인 구간을 묶는 DP 문제이다. 이러한 구간을 묶는 DP 문제를 만났을 때 대략 90프로 확률로 2가지 접근법을 생각해 볼 수 있습니다.
- d[i][j]로 i부터 j까지의 구간을 묶는 방법
- d[i]로 처음부터 i까지의 구간을 묶는 방법
위와 같이 2가지가 있지만 대부분의 경우 2번의 일차원 배열이 많이 사용되니 이 문제를 통해 문제 접근 방법의 틀을 만드는 것도 좋은 방법이라고 할 수 있습니다.
그럼 2번을 통한 접근 방법을 알아보겠습니다.
- d[i]를 i까지에 대한 답이라고 생각하겠습니다.
즉 i번째 학생까지 조를 짜서 구한 최대값을 의미합니다.
- d[i]를 i까지에 대한 답이라고 생각하겠습니다.
- dp 는 마지막에 초점을 두고 관찰하는것이 좋습니다. 마지막에 학생을 추가한다고 생각해봅니다.
- i번째 학생을 추가한다고 하고 모든 0 ~ i-1 범위의 j에 대해 아래와 같이 돌면서 최대값을 구하면 i번째 학생을 포함한 최대값이 됩니다.
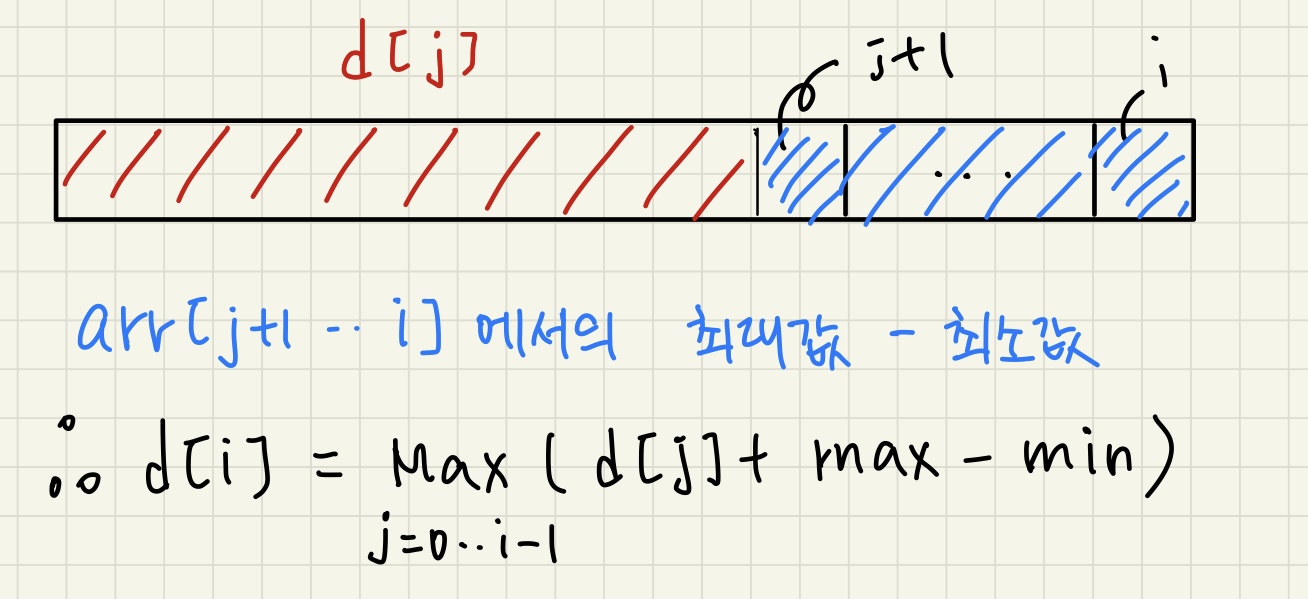
- i번째 학생을 추가한다고 하고 모든 0 ~ i-1 범위의 j에 대해 아래와 같이 돌면서 최대값을 구하면 i번째 학생을 포함한 최대값이 됩니다.
-
- 정리해보자면 구간을 묶는 dp의 경우 큰 문제와 동일한 작은 문제를 만들고 작은 문제에 마지막을 추가해가면 큰 문제를 찾는 것이라고 생각해주면 됩니다.
-
- 시간복잡도
배열의 크기 * 원소 하나를 구하는데 참고하는 개수 =>
- 시간복잡도
코드
import java.io.*;
import java.util.*;
class baek__2229 {
static int[] d;
static int[] arr;
static int go(int i) {
if (i <= 0) {
return 0;
}
if (d[i] != -1) {
return d[i];
}
d[i] = 0;
int max = arr[i];
int min = arr[i];
for (int j = i - 1; j >= 0; j--) {
max = Math.max(max, arr[j]);
min = Math.min(min, arr[j]);
d[i] = Math.max(max - min + go(j - 1), go(i));
}
return d[i];
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
arr = new int[n];
String[] temp = br.readLine().split(" ");
for (int i = 0; i < n; i++) {
arr[i] = Integer.parseInt(temp[i]);
}
d = new int[n];
Arrays.fill(d, -1);
System.out.print(go(n - 1));
}
}
