알고리즘

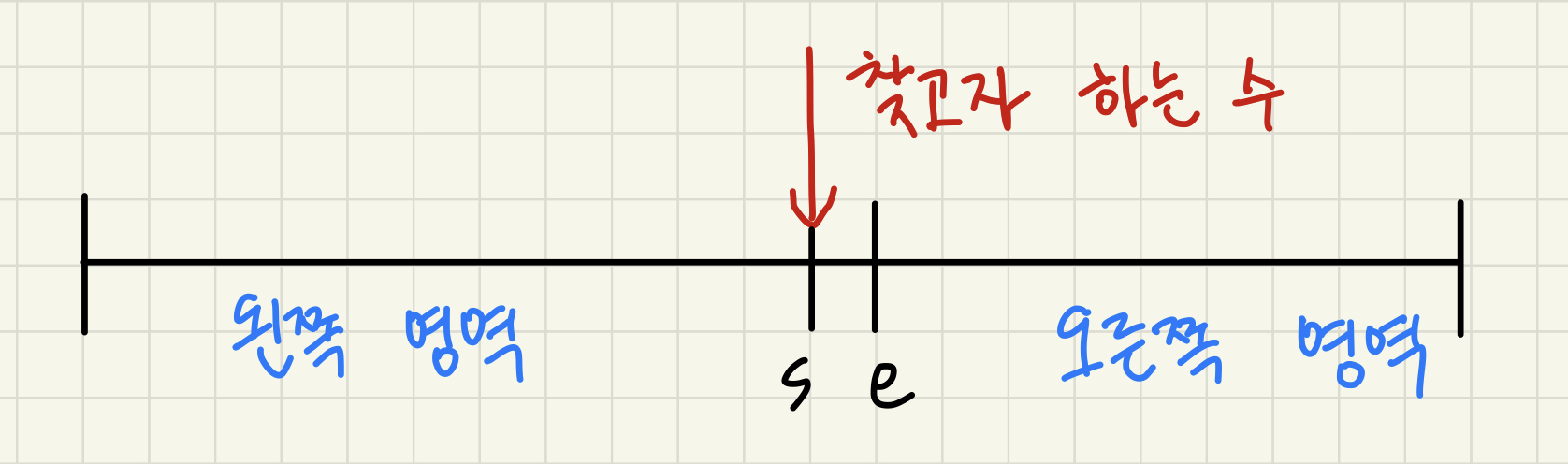
이분 탐색을 좀 더 쉽게 구현할 수 있는 방법을 작성하고자 합니다. 먼저 문제 하나를 제시합니다. BOJ-수 찾기 일반적 구현

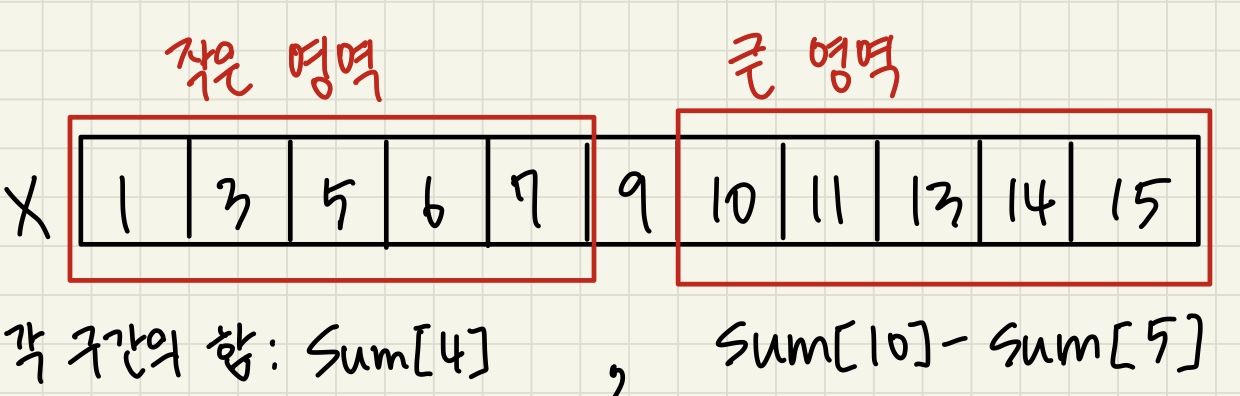
백준 16210 문제를 풀며 나누어 생각하는 것에 대해 이야기를 나누어보겠습니다.브루트포스특정 점에 대해 모든 점에 대한 거리를 구하고 그 중 최소값을 구한다. 복잡도 각각의 점에 대해 모든 점을 돌아야하므로 $o(n^2)$인데 문제에서의 n제한은 50만이다. 따라서

문제 배경을 보면 모든 어린이의 첫날 키는 0이고 각 어린이마다 키가 1씩 크는 날이 주어집니다. 이런 상황에서 i 어린이와 j어린이가 키 제한이 있는 k놀이기구를 탈 수 있냐는 q개의 질문이 주어지고 정해진 기간동안 각 날짜마다 몇 개의 질문에 대해 그렇다를 답할 수

문자열 s와 t가 주어지고 줄임말이라는 정의(b는 a의 줄임말이라고 하면 a 문자열 순서는 건드리지 않고 몇개의 문자를 제거하거나 제거하지 않았을때 b와 동일한 문자열을 만들 수 있어야 합니다)가 주어집니다. 이럴 때 문자열 t를 최소 몇개 이어붙여야 s가 줄임말이 되

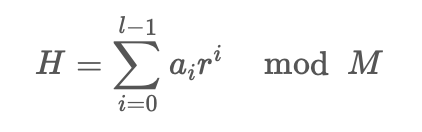
15829문제는 해시 함수를 설명하는 문제로 문제를 읽고 해시함수를 구현하면 쉽게 해결가능합니다.

터널에 들어간 순서와 나온 순서가 같아야 한다. 즉 추월을 해서는 안된다. 들어간 순서와 나온 순서를 알고 있을 때 반드시 추월한 차량의 수를 구하는 문제1\. 들어간 차량의 번호판과 순서를 각각 key 값과 value로 HashMap에 저장한다. 2\. 나온 차량의

문자열 s가 주어질 때 각각의 쿼리에 대한 F(i)값을 구하는 문제로 F(i)의 정의는 문자열 s와 s의 부분 문자열 s.substring(0, i+1)의 공통 접미사의 길이를 의미한다.문자열 s의 길이 N <= 1000000쿼리의 개수 M <= 100000

Boggle이라는 보드 게임에서의 최대 점수를 얻는 방법을 찾는 문제로 유의 사항으로는 10초라는 시간 제한이 있다는 점입니다. 10초가 아니라면 해결 방법이 있는지는 모르겠습니다.단어의 수 w < 300000보드의 개수 b < 30주어진 단어를 Trie 자

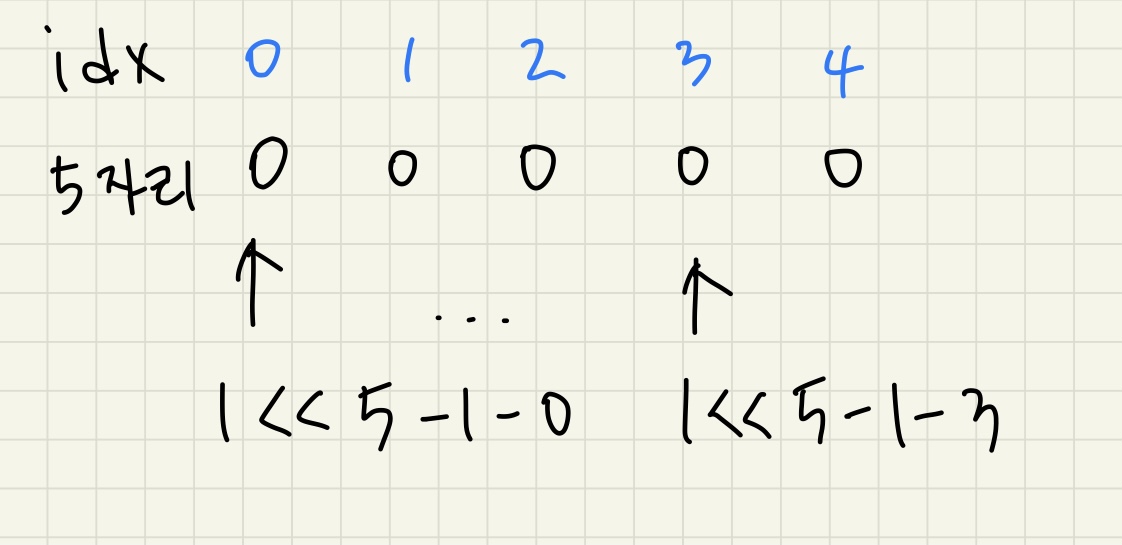
주어진 수 중에서 두 수를 골라 XOR 연산 결과를 구하고 그 결과의 최대값을 구하는 문제모든 수를 31비트의 이진수로 변환하여 Trie에 문자열로 저장한다. (길이를 모두 통일시키기 위해 31비트)각 수에 대해 Trie search 함수를 진행한다. 진행하는데 sea

주어진 수열의 연속된 부분 수열 중에서 XOR 합이 가장 큰 부분 수열의 XOR합을 구하는 문제테스트 케이스 t < = 10배열의 크기 N <= 100000모든 부분수열의 XOR합을 구해보는 $O(tN^2)$는 문제에 적합하지 않다.0부터 배열의 마지막 인덱

영문 소문자로만 이루어진 문자열 s와 t 2개가 주어지고 두 문자열의 어떤 특정한 구간에 존재하는 문자의 종류와 개수가 동일하면 두 구간 성분이 동일하다고 한다. 가장 긴 구간 성분의 길이를 구하는 문제 1<=$|s|,|t|$<=1500만약 모든 구간에 대해

부분 수열의 합이 M이 되는 경우의 수를 구하는 문제이다.두 포인터를 다루는 기본적인 문제로 개념 설명을 하도록 하겠습니다.두 포인터를 사용하기 위한 조건포인터 i가 움직이면 커져야 한다.(구간의 합이)포인터 j가 움직이면 작아져야 한다.(구간의 합이)결국 수열 중에

산성 용액과 알칼리성 용액의 특성값이 배열로 주어질때 두 용액의 특성 값의 합이 0에 가장 가까운 경우를 찾는 문제입니다.(절대값이 작으면 되겠죠?)전체 용액의 수 <= 100000이중 for문을 사용했다간 100억이라는 숫자를 맞을 테니 이중 for문을 대체할

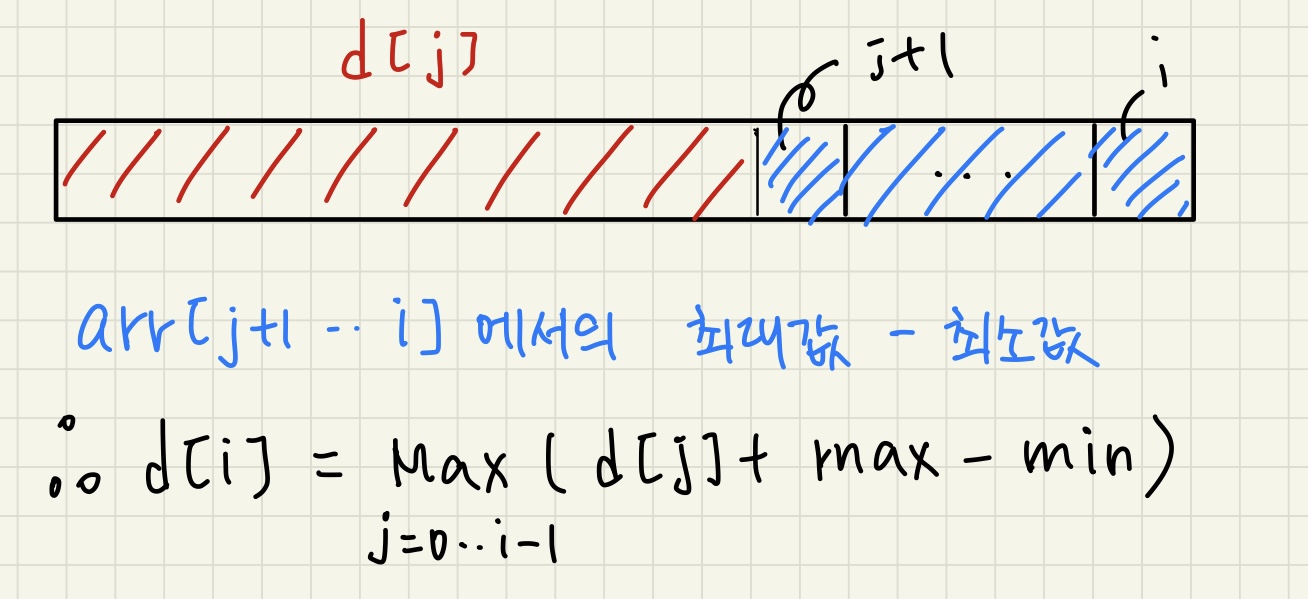
학생들의 점수가 배열로 주어지고 모여있는 학생끼리(문제에선 나이) 모아 조를 만드는데 조를 이룬 학생들의 점수 중 최대 점수와 최소 점수의 차이가 잘 짜여진 정도라고 정의한다. 조를 임의로 구성했을 때 잘 짜여진 정도의 합의 최대값을 구하는 문제입니다.학생 수 1 &l

LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제입니다.각 문자열의 길이 <= 1000LCS는 매우 유명하고 접근이 전형적이기 때문에 어떻게 접

자연수 N을 2의 멱수의 합으로 나타내는 경우의 수를 구하라.1 <= N <= 1000000$dN$을 $2^M$까지 포함 가능하여 N을 만들 수 있는 경우의 수로 정의합니다. 그리고 다음과 같은 점화식을 세워 봅니다. $dN = \\sum\_{j=0}^{M}

서윤이의 최대 공부시간 N이 주어지고 각 과목에 필요한 공부시간과 중요도가 주어진다. 최대 공부시간안에 가장 큰 중요도를 출력하는 문제입니다.최대 공부시간 1<= N <= 10000과목 수 1 <= K <= 1,000매우 전형적인 knapsack

문제는 요약하기가 쉽지 않아 링크 참고 바랍니다.1\. 정말 놀라운 사실은 바로 행과 열이 서로 영향을 미치지 않는다는 겁니다. 이게 어떤 말인지 알기 위해 이런 생각을 해봅니다. 1차원 배열이 있다고 생각하고 사탕 줍기 대회의 규칙과 비슷하게 사탕을 주으면 양 옆에

문제 실행중인 앱 중에서 재실행할 비용과 현재 점유중인 메모리가 주어지고 새로운 앱을 실행하기 위해 앱을 종료시킬 최소 비용을 구하는 문제입니다. 실행중인 앱의 개수 N 실행중인 앱을 종료하여 얻는 메모리 무게 => 실행중인 앱을 종료 후 재실할 때 필요한 비용

임의의 루트 있는 트리의 간선 정보가 주어질 때 정점을 주면 정점을 루트로 하는 서브 트리에 포함된 정점의 개수를 구하는 문제입니다.dfs를 사용할건데요. dfs를 작성할때 일반적으로는 check 배열이나 visited 배열을 사용해서 방문한 정점을 체크하실텐데요. 트

이진 탐색 트리는 한 노드를 기준으로 왼쪽 자식 노드를 루트로 하는 서브 트리의 모든 노드 값은 현재 노드보다 작은 값을 갖고 오른쪽 자식 노드를 루트로 하는 서브 트리의 모든 노드 값은 현재 노드보다 큰 값을 갖는다.삽입할 노드가 들어갈 위치를 찾고($O(logN)$

힙은 완전 이진 트리로 즉 마지막 레벨을 제외한 모든 레벨의 노드가 채워져 있는 트리로 최대 힙과 최소 힙 두 가지로 많이 사용됩니다. > B는 완전 이진 트리가 아니다. 최대 힙에 포함된 부모 노드는 자식 노드에 들어있는 값보다 크고 최소 힙에 포함된 부모 노드는

Union-Find는 자료구조 트리를 활용해 집합을 표현하는 자료구조이며 집합간의 합치거나(Union) 원소가 어느 집합에 포함되어 있는지를 찾는(Find) 연산이 매우 빠른 것이 특징입니다.빠르게 찾는 다는 것은 최적화가 이루어졌을 때 대부분의 경우에서 상수 시간의

최소 스패닝 트리란?(최소 신장 트리) 최소 스패닝 트리란 그래프(트리 아닙니다)의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 의미합니다. 의 그래프에서 최소 스패닝 트리는 의 형태를 띄게 됩니다. 가중치가 10인 경로는 제외되었습니다

k개의 소수가 있습니다. 이 소수들 중에서 몇개를 곱해 얻게 되는 수들을 정렬하여 n번째 수를 구하는 문제 입니다. 얻게 되는 수에는 주어진 소수 자체도 포함시킵니다. 소수 개수 k <= 100n <= 100000먼저 몇개의 소수를 곱해 얻을 수 있는 수를

[1] 그래프 조건, 트리 조건 사이클에 대해 이야기하기 전에 2가지 사실을 짚고 넘어갑니다. 1. 정점 n개, 간선 n-1개인 그래프는 트리이다. 그렇지 않습니다. 하지만 역인 트리이면 정점 n개 간선 n-1개를 갖는다는 맞습니다. 2. 정점 n개, 간선 n개인

투 포인터 알고리즘은 중첩 반복문(보통 $O(N^2)$for문 2개)을 $O(N)$의 복잡도로 수행할 수 있는 상황에 많이 쓰입니다. 상당히 매력적입니다. 포인터 2개니까 느낌적으로 중첩 반복문 역할을 수행하는구나 라는 생각이 들겠지만 저를 포함해서 아마 많은 분들이