<Trie> BOJ 13505 두 수 XOR

문제

주어진 수 중에서 두 수를 골라 XOR 연산 결과를 구하고 그 결과의 최대값을 구하는 문제

접근

• 1. 모든 수를 31비트의 이진수로 변환하여 Trie에 문자열로 저장한다.
     (길이를 모두 통일시키기 위해 31비트)
• 2. 각 수에 대해 Trie search 함수를 진행한다. 진행하는데 search함수가 조금 특이하다.
  • 2-1. XOR연산의 특징은 서로 다른 비트일 때 1이라는 결과를 얻는다는 것이다.
  • 2-2. 서로 다른 비트가 최대값을 얻는다는데에서 착안하여 0이라면 1을 찾고 1이라면 0을 찾는다.
  • 2-3. 반대 비트가 있다면 idx에 맞는 값을 더해준다.(코드 참고)
  • 2-4. 반대 비트가 없다면 같은 값을 찾고 더하는 과정은 없다.
  • 2-5. XOR 최대 값을 출력해준다.

주의 사항으로는 위의 방법으로 최대 연산 값을 구하기 위해서는 큰 자리수부터 찾아야 한다. 왼쪽에서 오른쪽으로 가라는 말입니다.

코드

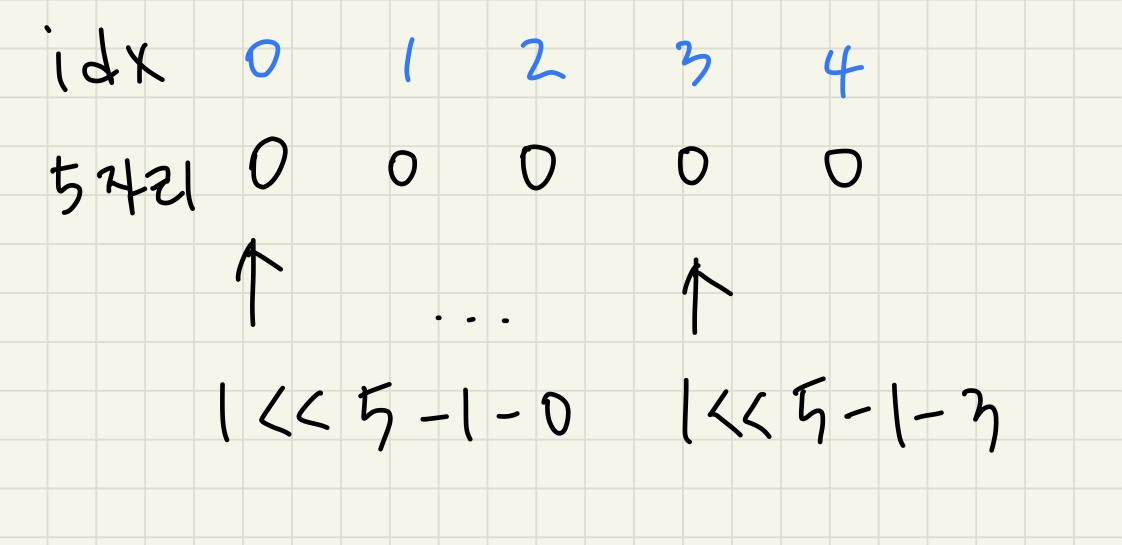
• search 함수를 다룰 때 몇 번째 index까지의 결과를 담아야 할지 헷갈린다면
  search(s, 0, root, 0)가 문자열 s의 0번째 index를 찾는 과정인데 answer에는 0이 할당 되어 있다. 즉 search(s, 1, node, answer)를 할때 answer에 s의 0번째 index까지에 대한 결과가 담기게 된다는 것이다. 따라서 idx+1을 해줄때 ans에 들어가야 하는 값은 idx번째 index까지에 대한 결과이다.
• trie의 search함수 구현을 보면 ans += (1 << s.length() - 1 - idx)부분이 있다.
  이 부분이 헷갈린다면 이렇게 생각해보자.
  

import java.io.*;
import java.util.*;

class Node {
    int[] children;
    boolean valid;

    Node() {
        children = new int[2];
        Arrays.fill(children, -1);
        valid = false;
    }
}

class Trie {
    ArrayList<Node> trie;
    int root;

    int init() {
        Node x = new Node();
        trie.add(x);
        return trie.size() - 1;
    }

    Trie() {
        trie = new ArrayList<>();
        root = init();
    }

    void add(String s, int idx, int cur) {
        if (idx == s.length()) {
            trie.get(cur).valid = true;
            return;
        }

        int c = s.charAt(idx) - '0';
        if (trie.get(cur).children[c] == -1) {
            int nex = init();
            trie.get(cur).children[c] = nex;
        }

        int nex = trie.get(cur).children[c];
        add(s, idx + 1, nex);
    }

    void add(String s) {
        add(s, 0, root);
    }

    int search(String s, int idx, int cur, int ans) {
        if (idx == s.length()) {
            return ans;
        }

        int c = 1 - (s.charAt(idx) - '0');
        if (trie.get(cur).children[c] == -1) {
            c = 1 - c;
        } else {
            ans += (1 << s.length() - 1 - idx);
        }
        int nex = trie.get(cur).children[c];
        return search(s, idx + 1, nex, ans);
    }

    int search(String s) {
        return search(s, 0, root, 0);// 0번째에 0이라고 생각하자.
    }
}

class baek__13505 {

    static String getBinary(int n) {
        String s = "";
        while (n >= 2) {
            s = (n % 2) + s;
            n /= 2;
        }
        s = n + s;
        while (s.length() < 31) {
            s = '0' + s;
        }
        return s;
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());

        Trie trie = new Trie();
        int[] nums = new int[n];

        String[] temp = br.readLine().split(" ");
        for (int i = 0; i < n; i++) {
            nums[i] = Integer.parseInt(temp[i]);
            String s = getBinary(nums[i]);
            trie.add(s);
        }

        // System.out.println(getBinary(2));
        // System.out.print(getBinary(trie.search(getBinary(2))));

        int answer = -1;
        for (int i = 0; i < n; i++) {
            String s = getBinary(nums[i]);
            int comp = trie.search(s);
            answer = answer == -1 ? comp : Math.max(answer, comp);
        }

        System.out.print(answer);

    }
}