[1] 그래프 조건, 트리 조건
사이클에 대해 이야기하기 전에 2가지 사실을 짚고 넘어갑니다.
1. 정점 n개, 간선 n-1개인 그래프는 트리이다.
그렇지 않습니다. 하지만 역인 트리이면 정점 n개 간선 n-1개를 갖는다는 맞습니다.
2. 정점 n개, 간선 n개인 그래프는 정확히 한개의 사이클을 갖는다.
맞습니다. 간선의 개수가 정점의 개수와 같다면 하나의 사이클이 존재하게 됩니다.
그렇다면 사이클을 어떻게 찾을 수 있을까요?
[2] 사이클을 찾기 위해 필요한 2가지
1. DFS로 그래프를 탐색하고나서 탐색 경로를 살펴보면 트리가 된다.
<주어진 그래프>
<DFS 경로를 표시한 그래프>
주어진 그래프를 딱보면 사이클이 있는 그래프네요. 이 그래프를 정점 1을 루트로 DFS 탐색을 하고 탐색한 경로를 빨간색으로 표시한것이 아래 이미지입니다. 빨간색 이미지를 보면 어떻나요? 트리를 이루고 있죠? 트리의 정의는 무엇인가요? 임의의 두 노드를 잇는 경로는 유일해야하죠. DFS는 어떤가요? 같은 노드를 여러번 방문하나요? 그렇지 않죠 그래서 DFS경로를 표시하면 위와 같이 트리가 됩니다.
2. 트리는 어디서부터 왔는지를 이용하면 visited배열 없이 DFS 탐색이 가능하다.
DFS 탐색시에 많은 분들이 visited 배열을 이용해서 방문한 노드를 확인하는데 사용하실거라 생각합니다. 그런데 트리에서는 visited 배열 없이도 DFS탐색을 할 수 있습니다. 현재 탐색 중인 노드의 부모를 표시하면 가능합니다. 다음 방문할 노드가 현재 노드의 부모라면 다시 방문하지 않는것이죠.
코드로는 아래와 같이 직전 노드가 어디인지만 표시해주면 됩니다.
dfs(int now, int from){
for(int next : list[now]){
//다음에 방문할 노드가 현재 노드의 부모라면 방문하지 않는다.
if(next == from){
continue;
}
dfs(next, now);
}
}
// dfs를 시작할때는 자기 자신을 부모로 해줘도 됩니다.
dfs(1,1);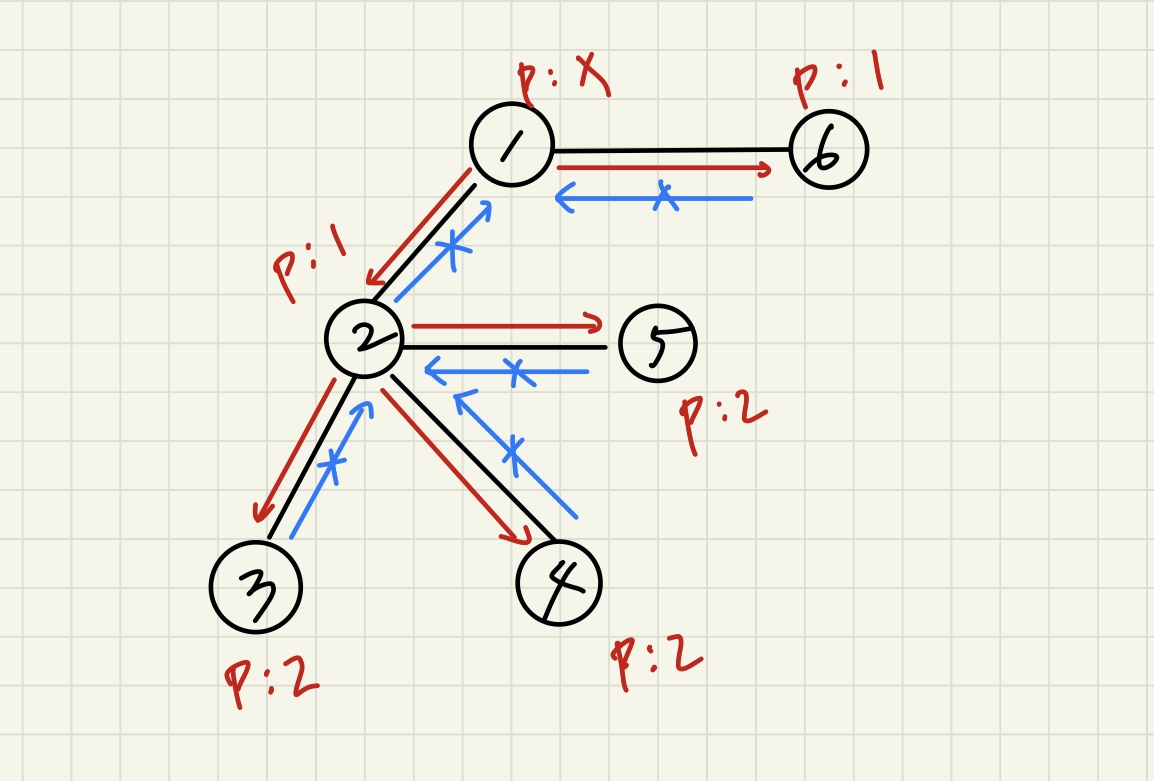
위 그래프에서 빨간색은 실제 탐색 경로를 나타내면 파란색은 탐색을 시도했으나 부모와 같아서 방문하지 않은 것을 의미합니다.
[3] 사이클 찾기
그럼 이제 우리는 사이클을 찾는데 필요한 두가지 조건을 모두 알았습니다. 이제 사이클을 찾고 사이클에 존재하는 정점을 모두 출력해보도록 하겠습니다.
먼저 조건은 정점 n개, 간선 n개를 갖는 그래프입니다. 우리가 위에서 배운대로 무조건 한개의 사이클을 갖습니다. 우리는 이 그래프를 DFS탐색을 할 겁니다. 탐색을 하기 위해 우리는 visited배열과 노드의 부모 노드 표시 두가지를 사용할 겁니다. 탐색 경로로 우리는 트리를 얻게 될 겁니다.
이제 사이클을 찾기 위해 한가지 트릭을 더합니다. 우리는 그래프를 찾기 위해 n-1개의 간선을 탐색했을 것이고 남은 1개의 간선이 바로 사이클을 찾는 키가 됩니다. 부모 노드와 다음 노드를 이용해 표시했음에도 visited한 정점을 발견한다면 바로 정점에 의해 사이클이 형성된 것이란걸 알 수 있습니다.
이 상황에선 1번 정점과 6번 정점을 잇는 간선이 사이클을 형성한 원인이 되겠죠. 이 간선만 없다면 트리였으니까요. 우리가 이런 정점을 찾았을 때 이 간선을 잇는 두 정점을 표시해두면 이제 우리는 사이클의 끝과 끝을 찾은 겁니다.
끝과 끝을 찾았지만 갈길이 멀군요.. 사이클에 포함된 정점들은 어떻게 찾을 까요? 바로 아래와 같이 찾을 수 있습니다. 방문할 때마다 이 정점이 어디서부터 온지를 저장해놓으면 돼요.
6은 5에서 왔고 5는 2에서 왔고 2는 1에서 왔고 1은 사이클의 끝과 끝이니까 더 확인할 정점은 없다. 따라서 1, 2, 5, 6이 사이클을 이루는 정점이다 라는 결론을 얻을 수 있습니다.
[4] 관련 문제
서울 지하철 2호선 이라는 문제 입니다. 위에 적힌 설명과 BFS에 대한 지식이 있다면 충분히 해결가능하니 꼭 풀어보시기 바랍니다. 사실 이 포스트를 적게 된 원인이 된 문제입니다. 여러번 풀어보았는데 풀때마다 새로운 실수를 해서 반나절씩 시간을 잡아먹더라구요.. 뭔가 희한한 문제입니다. 차근히 풀어보시면 쉽게 푸실거라 생각합니다. 이걸 풀고나면 지하철 탈 때 재밌습니다. ㅋㅋㅋ
