<이분 탐색> 구현 방법

이분 탐색을 좀 더 쉽게 구현할 수 있는 방법을 작성하고자 합니다.
먼저 이분 탐색 기초 문제 하나를 제시합니다. BOJ-수 찾기

일반적 구현

우선 입출력은 생략하였는데 이분 탐색을 위한 전제조건으로 배열 nums는 오름차순으로 정렬되어있어야 합니다. start와 end를 배열의 왼쪽 끝과 오른쪽 끝 인덱스로 초기화하고 이분 탐색을 진행합니다. 이분 탐색을 위해 총 세개의 조건을 사용했고 각 조건마다 아래와 같은 동작이 따릅니다.

1. target보다 큰 경우
   end를 mid보다 1작은 수로 바꾼다.
2. target과 동일한 경우
   찾았으므로 1을 return하고 종료.
3. target보다 작은 경우
   start를 mid보다 1큰 수로 바꾼다.

간단하다고 생각할 수 있지만 각 조건을 위한 사고가 조금은 필요합니다.

static int go(int[] nums, int target){
  int start = 0;
  int end = nums.length-1;
  
  while(start <= end){
    int mid = (start+end)/2;
    
    if(nums[mid] > target){
      end = mid-1;
    }else if(nums[mid] == target){
      return 1;
    }else if(nums[mid] < target){
      start = mid+1;
    }
  }
  
  return 0;
}

간단한 구현

간단한 구현은 start와 end의 초기점을 절대 검사하지 않기 때문에 start와 end에 대한 초기화를 배열 밖의 가상의 점으로 만들어 줍니다.

• start : -1
• end : nums.length

우리가 찾는 수가 어떤 칸에 있다고 생각하고 그 칸을 기준으로 두 개의 영역으로 나누어봅니다. 왼쪽 영역은 우리가 찾는 target보다 작거나 같은 수를 담고 있고 오른쪽 영역은 우리가 찾는 target보다 큰 수를 담고 있습니다. mid를 구하고 그 mid에 해당하는 수가 왼쪽 영역에 해당한다면 start를 mid로 오른쪽 영역에 해당한다면 end를 mid로 옮겨줍니다. 이분 탐색이 종료되는 시점의 start와 end의 위치를 그림으로 표현하면 아래와 같습니다.

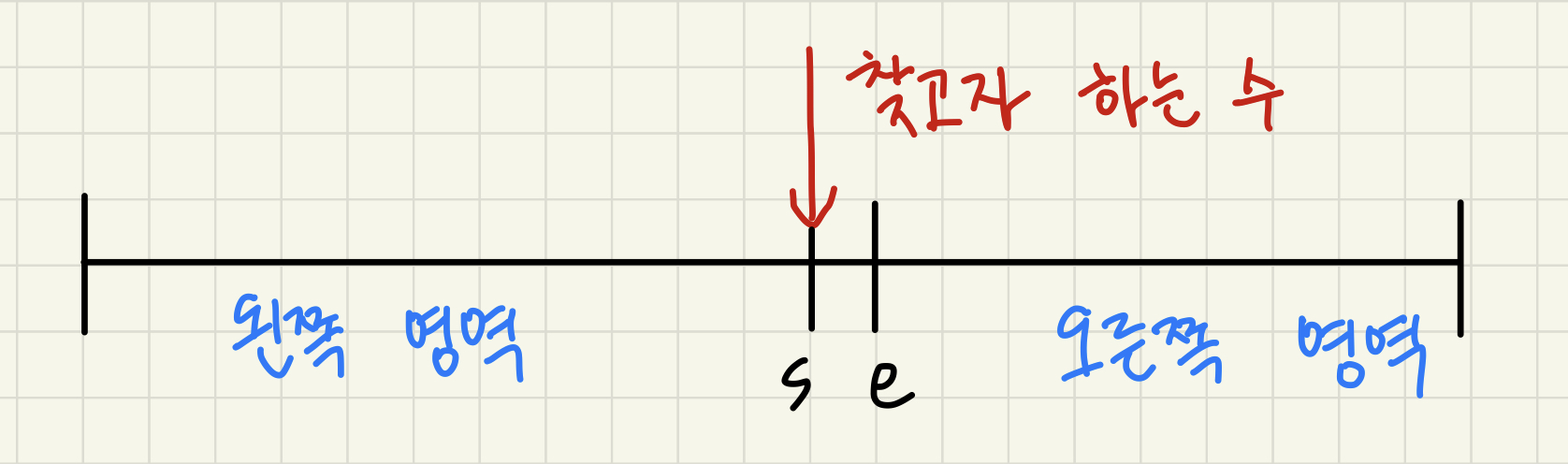
따라서 while문 종료 조건도 조금 다릅니다. start+1 == end가 될 때까지 while문을 돌리게 됩니다. (한 칸 차이가 날 때까지 돌립니다. s와 e는 서로의 영역을 절대 침범할 수 없습니다.)

static int go(int[] nums, int target){
  int start = -1;
  int end = nums.length;
  
  while(start+1 < end){
    int mid = (start+end)/2;
    
    if(nums[mid] <= target){
      start = mid;
    }else{
      end = mid;
    }
  }
  
  return nums[start] == target? 1 : 0;
}

코드를 보면 start와 end를 옮기는 과정에서 mid+1과 mid-1이라는 과정이 빠지면서 상당히 간결해지고 사고가 쉬워졌습니다. 이제 그럼 이 코드를 이용해서 upper_bound와 lower_bound도 구현해보겠습니다.

upper bound

upper bound는 target값보다 큰 수 중 첫번째 위치를 반환해야합니다. 정의를 생각하면 사실 우리는 이미 upper bound를 구했습니다. 바로 end의 위치가 upper bound입니다.

• target이 nums 배열에 있는 모든 수보다 크다면
  end는 한번도 움직이지 않았을 것이고 nums.length를 출력합니다.
• target이 nums 배열에 있는 모든 수보다 작다면
  start가 한번도 움직이지 않았을 것이고 end는 마지막에 0을 가리킬 것입니다.
• target이 nums배열에 여러개 있었다면
  end는 동일한 수 중 가장 왼쪽에 있는 수를 가리키고 있습니다.
  모든 경우에 대해서 upper bound 조건을 만족하고 있습니다.

static int upper_bound(int[] nums, int target){
  int start = -1;
  int end = nums.length;
  
  while(start+1 < end){
    int mid = (start+end)/2;
    
    if(nums[mid] <= target){
      start = mid;
    }else{
      end = mid;
    }
  }
  
  return end;
}

lower bound

lower bound는 target값보다 크거나 같은 수 중 첫번째 위치를 반환해야합니다. 우리가 만들었던 두 영역에 대한 조건을 조금 바꿔봅니다.

• 왼쪽 영역
  target보다 작은 수를 담고 있는 영역
• 오른쪽 영역
  target보다 크거나 같은 수를 담고 있는 영역
  이렇게 나누어주면 탐색이 끝나고 난 후 end가 가리키고 있는 곳이 lower_bound가 됩니다. while문이나 초기값은 모두 동일하게 해줍니다.

static int lower_bound(int[] nums, int target){
  int start = -1;
  int end = nums.length;
  
  while(start+1 < end){
    int mid = (start+end)/2;
    
    if(nums[mid] < target){
      start = mid;
    }else{//>= target
      end = mid;
    }
  }
  
  return end;
}

이렇게 해서 좀 더 직관적인 이분 탐색을 알아보았고 상황에 따라 영역에 대한 조건을 바꾸면 이분 탐색 관련 모든 문제에서 위의 테크닉을 사용할 수 있습니다.

감사합니다.