이 글은 2021.04.18에 작성했던 코딩 테스트 문제 풀이를 재 업로드한 게시물입니다.
문제 설명
- 문제 : 백준 1074
이 문제는 의 크기를 가진 2차원 배열을 특정 규칙에 따라 각 칸을 방문하고, 그 순서대로 0부터 번호를 새긴 다음 r행 c열의 값을 찾아내는 문제입니다. 문제에서 설명된 바와 같이 작은 사각형부터 큰 사각형까지 모두 Z방향으로 방문하면 됩니다.
사전 지식
이 문제는 재귀에 대한 기본적인 지식만 있으면 풀 수 있기 때문에 별도의 설명을 하지는 않겠습니다.
접근 방법
아주 단순한 접근
코딩을 제대로 배우기도 전에 이 문제를 접하고, "재귀를 이용해 모든 칸을 다 채운 다음에 r행 c열의 값을 알면 되지 않을까?"라고 생각했습니다.
그럴듯해 보이는 접근이었지만 가장 중요한 것을 간과했습니다. 개의 칸을 모두 다 채워야 하는데 이러면 시간 및 공간 복잡도가 이 될 것이기 때문이죠. 굉장히 무식했던 이 방법은 결국 메모리 초과로 인해 실패로 돌아갔습니다. 당시에 짰던 C 코드 일부는 다음과 같습니다.
void MarkArr(int** arr, int size, int st_row, int st_col) {
if (size == 1)
arr[st_row][st_col] = cnt++;
else {
MarkArr(arr, size / 2, st_row, st_col);
MarkArr(arr, size / 2, st_row, st_col + size / 2);
MarkArr(arr, size / 2, st_row + size / 2, st_col);
MarkArr(arr, size / 2, st_row + size / 2, st_col + size / 2);
}
}분할과 선택
실패를 겪고 난 후, 다시 이 문제를 풀 때 접근 방법의 잘못된 점을 찾아냈습니다. 그것은 바로 필요 없는 정보가 너무 많다는 것이었습니다.
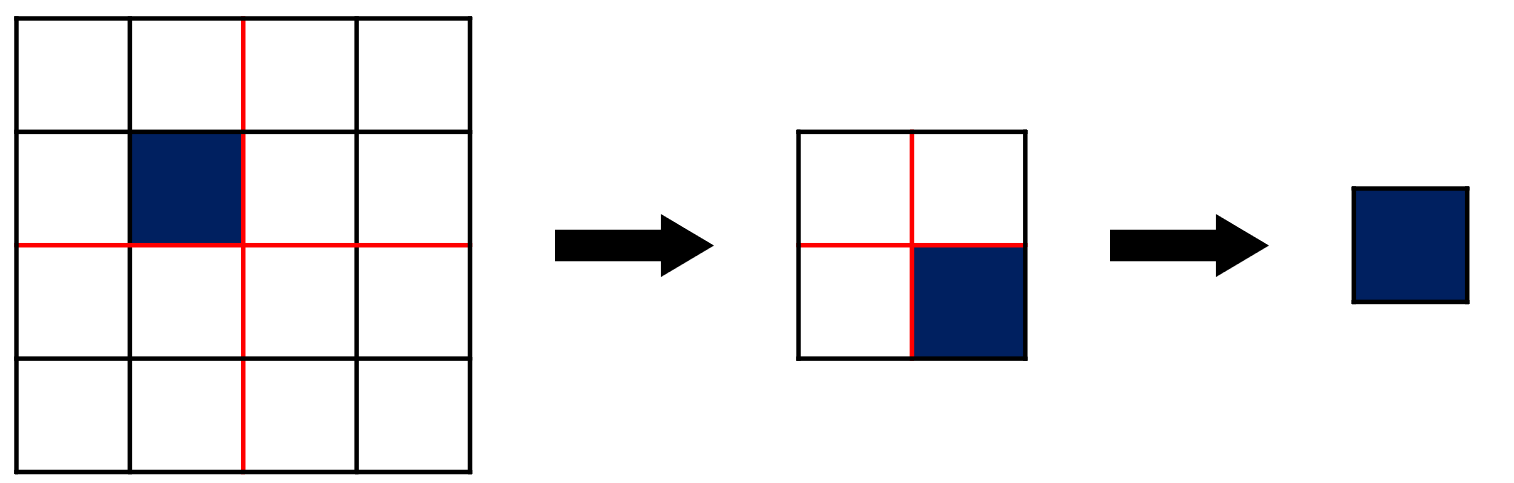
한 정사각형에서 왼쪽 위, 왼쪽 아래, 오른쪽 위, 오른쪽 아래 작은 네 개의 정사각형으로 나뉘는데 이 중 우리가 필요한 r행 c열의 정보는 한 개의 작은 정사각형에만 있다는 걸 생각해 봤습니다.
모든 칸을 다 채울 필요 없이, 필요한 칸의 값만 알면 공간 및 시간을 적게 쓰고도 문제를 풀 수 있습니다. 큰 정사각형을 네 개의 1/4 크기의 정사각형으로 분할한 후 그중 찾고자 하는 행과 열의 작은 정사각형을 선택하면 됩니다. 이 과정을 가장 작은 칸 한 칸이 남을 때까지 재귀적으로 반복하면 됩니다. 그림으로 설명하면 다음과 같습니다.
여기서 주목해야 할 점은 두 가지입니다. 첫 번째는 위 그림과 같이 작은 정사각형을 선택하게 되면, 행과 열의 값을 어떻게 바꿔야 하는가? 두 번째는 위와 같이 사각형을 선택하는 과정에서 번호를 어떻게 세야 하는가?
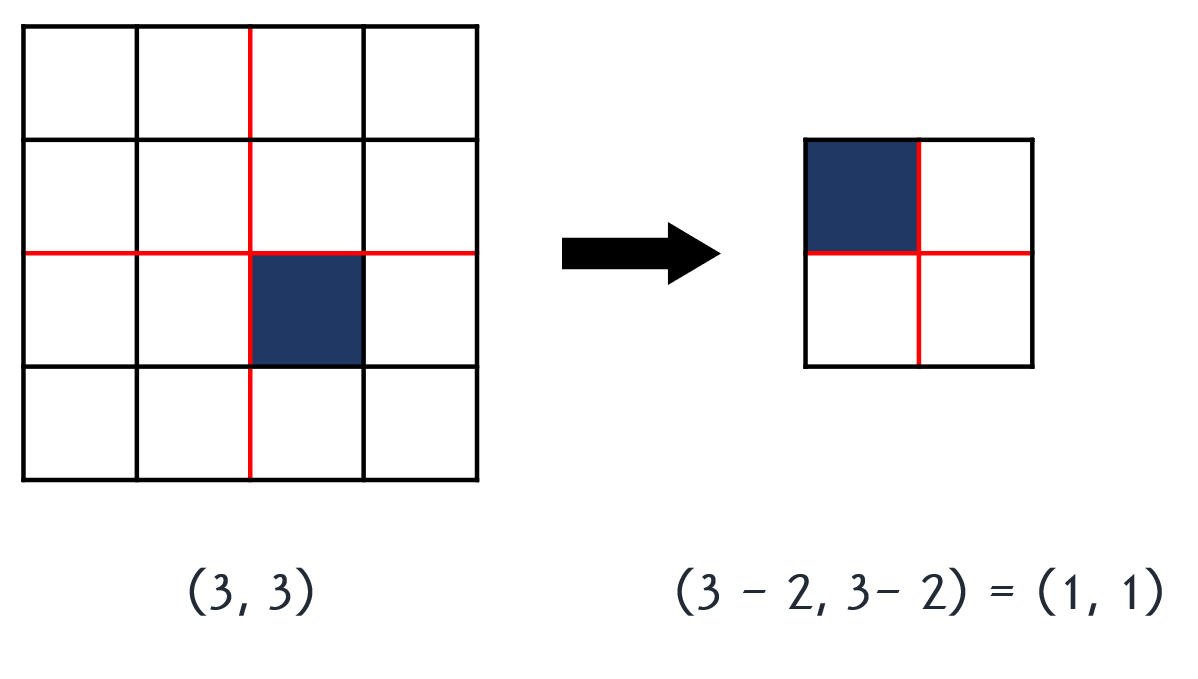
행과 열의 값을 바꾸는 것은 쉽습니다. 만약 오른쪽에 있는 정사각형을 택했다면, 열 값을 원래 값에서 "작은 정사각형의 한 변의 길이"만큼 빼 주면 됩니다. 아래쪽인 경우 행에서 그만큼 빼 주면 됩니다. 일종의 평행이동 개념으로 봐도 될 듯합니다.
위 그림에서 볼 수 있듯이 큰 정사각형에서 3행 3열인 칸은 작은 정사각형에서 1행 1열의 칸이 됩니다.
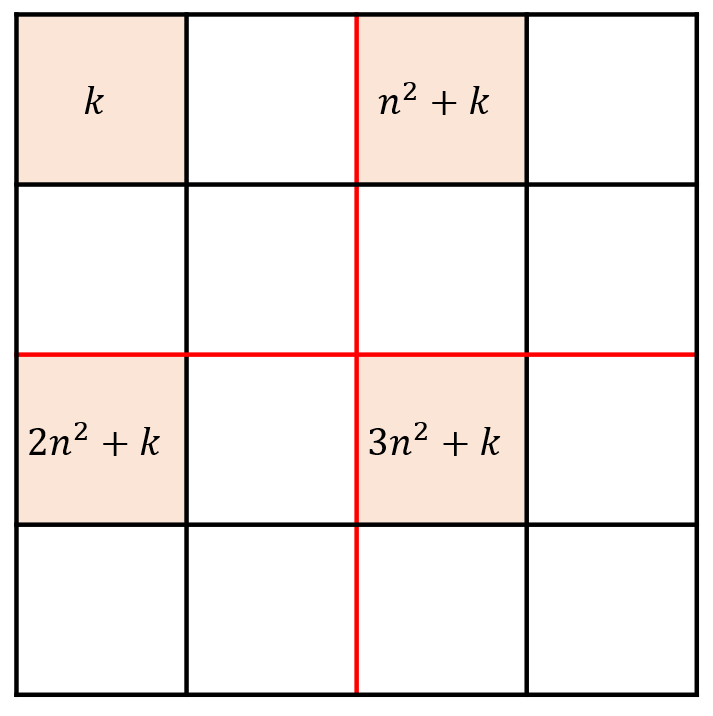
번호를 세는 것 역시 쉽게 생각해낼 수 있습니다. 작은 정사각형의 한 변의 길이를 n이라고 하면 왼쪽 위 정사각형과 오른쪽 위 정사각형의 번호를 비교해 봅시다. 오른쪽 위 정사각형의 r행 c열의 번호는 왼쪽 위 정사각형의 r행 c열의 번호 + 이 됩니다. Z 모양이므로 왼쪽 아래, 오른쪽 아래는 각각 , 이 됩니다. 다음 그림과 같습니다.
즉, 정사각형의 위치를 파악해 오른쪽 정사각형에 있으면 번호에 을 더하고, 아래쪽 정사각형에 있으면 번호에 을 더하면 됩니다.
코드 설명
목표로 하는 열과 행, 현재 정사각형의 한 변의 길이, 현재까지 더한 번호들의 합을 인수로 받아서 재귀적으로 칸의 번호를 찾는 함수 Z_calc를 이용해 문제를 풀었습니다.
각 행을 row, 열을 col, 현재 정사각형의 길이를 N, 총합을 idx라는 인수로 받았습니다. 여기서 idx는 현재까지 더한 모든 값을 저장하는 인수입니다. 만약 현재 정사각형의 길이가 1이라면, 현재 칸이 문제에서 요구한 칸이므로 더한 결괏값인 idx를 반환합니다.
int Z_calc(int row, int col, int N, int idx){
if(N == 1)
return idx;현재 정사각형의 길이가 1이 아니면, 작은 정사각형의 길이를 구한 후 이를 N에 다시 대입합니다. 이후 현재 행 값이 N보다 크다면 4 분할 한 정사각형의 아래쪽에 있다는 의미이므로, 을 더해줍니다. 그리고 행의 상대적 위치가 변경되므로, 즉 N값만큼 행에서 빼 줍니다. 열에 대해서도 똑같은 작업을 수행하되, 이 경우에는 idx에 을 더해줍니다. 이후 재귀적으로 작은 정사각형으로 내려갑니다.
exp_N /= 2;
if(row > N){
row -= N;
idx += (N * N) * 2;
}
if(col > N){
col -= N;
idx += (N * N);
}
return Z_calc(row, col, N, idx);이때 각 행과 열은 1부터 시작한다는 가정하에 구성되어있습니다. 그런데 문제에서는 0부터 시작하는 행과 열을 주기 때문에 다음과 같이 호출해서 결과를 출력하면 됩니다.
printf("%d\n", Z_calc(row + 1, col + 1, N, 0));마치며
재귀를 간단히 이용하므로 쉬어가는 문제로 풀어가기 좋습니다. 코드 원본은 여기를 참고해 주시면 됩니다.