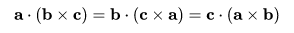01.30

Mouse Picking

Screen space의 Mouse position을 사용하여 Client 공간에 Rendering되어있는 3D Object를 선택하거나 교점을 찾는 것

선택

Object 자체를 선택

교점

Object와 cross된 정확한 위치 반환

좌표계 일치

Object는 Local->World->View->Projection->Screen 순서로 정점이 변환되는데 이 때 Mouse의 Ray와 Object의 좌표계가 일치해야 한다
일반적으로 가장 큰 데이터를 차지하는 Map vertex정보가 World를 기준으로 배치되어있으므로 Mouse의 Ray를 World로 변환하는 것이 좋음

Viewport Matrix

Projection Space에서 Screen 좌표로 변환하기 위해서는 Viewport Matrix를 사용

Width, Height = Viewport 세로 크기
X, Y = 뷰 포트 시작 위치

이 때, 일반적으로 X, Y의 값을 0으로 지정(Viewport와 Client의 크기가 동일한 경우)하므로 Viewport Matrix의 역행렬은 더 간단하게 구해질 수 있음

이 때 Projection Matrix는 다음과 같고

오른쪽 식은 Viewport의 Width, Height 사용

Projection Matrix의 $a_{11}$, $a_{22}$만 정점에 영향을 미치므로 View Space Ray Direction은 다음으로 간단하게 치환할 수 있음
$V_{x} = (\frac{2 * Screen_{x}}{Width} - 1) * \frac{1}{W}$
$V_{y} = (\frac{-2 * Screen_{y}}{Height} - 1) * \frac{1}{H}$
$V_{z} = 1$
그런데 Width=W, Height=H아닌가?
작업중

이제 View Space를 World Space로 변환해야 함

D3D에서는 동차변환을 위해 D3DXVec3TransformCoord와 D3DXVec3TransformNormal을 지원하는데 Coord의 경우 w = 1로, Normal의 경우 w = 0으로 설정한다

교점 계산

외적 사용법

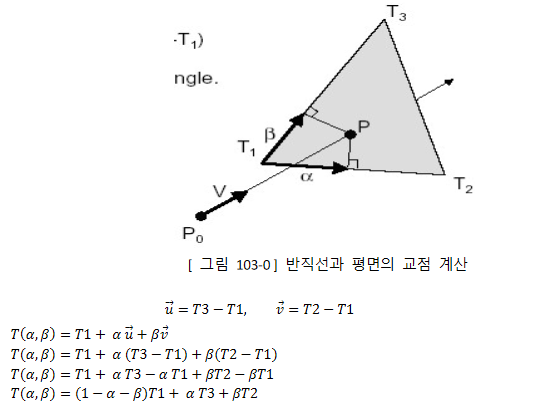
교점 계산

평면 법선 벡터 $\vec{N}$과 평면위의 한 점 $V$, Ray의 시작과 끝점인 $\vec{V_{o}}, \vec{V_{e}}$를 내적을 통해 길이 A, t를 구하면 그 비율 $r$을 구할 수 있음

교점 판정

$V_{0}, V_{1}, V_{2}, V_{Inter}$를 동일한 edge순서($E_{01}\cdot{E_{V_{0I}}}, E_{12}\cdot{E_{V_{1I}}}, E_{21}\cdot{E_{V_{2I}}}$)로 각각 외적을 취할때, 만약 $V_{Inter}$가 $V_{0}, V_{1}, V_{2}$안에 있다면 모두 동일한 방향으로 외적이 생성될 것이다
즉, 이 때 생성된 $\vec{N}\cdot\vec{F}$의 값이 동일(양수 또는 음수)라면 정점은 삼각형 내부에 포함된다

UV 매개변수 사용법

외적 사용법은 해법이 간단하지만 외적 연산량이 매우 많아서 비효율적임

이를 통해 $0 \le \alpha, 0 \le \beta, \alpha + \beta \le 1$를 알 수 있음

위 식을 정리하면

이 때, $O-T_{1} = T$로 가정한다면

이제, 위 식을 33행렬의 역행렬과 Cramer 법칙, 삼중곱을 이용하여 정리하면

Reference : https://ko.wikipedia.org/wiki/%ED%96%89%EB%A0%AC%EC%8B%9D

Reference : https://ko.wikipedia.org/wiki/%EC%82%BC%EC%A4%91%EA%B3%B1

Reference : https://ko.wikipedia.org/wiki/%ED%81%AC%EB%9D%BC%EB%A9%94%EB%A5%B4_%EB%B2%95%EC%B9%99

삼중곱

위와 같이 정리된다

이를 통해 $D\times{E_{2}}, T\times{E_{1}}$ 단 2번의 외적 계산만으로 교점의 위치, u, v의 값을 모두 구할 수 있음

각 항의 의미

det

$det = \frac{1}{E_{1}\cdot(D \times E_{2})}$
Ray의 Normal Vector $\vec{D}$와 삼각형의 한 edge인 $E_{2}$의 외적을 통해 평면 $\vec{N}$을 구한 후, 삼각형의 한 edge인 $E_{1}$과의 내적을 통해 삼각형의 높이값 계산

u

$u = \frac{\vec{T} \cdot (\vec{D} \times \vec{E_{2})}}{E_{1}\cdot(D \times E_{2})}$
$\vec{N} \cdot \vec{T}$를 통해 $u$를 구한 후 $\frac{u}{det} = \alpha$

v

$v = \frac{\vec{D} \cdot (\vec{T} \times \vec{E_{1}})}{\vec{E_{1}} \cdot (\vec{D} \times \vec{E_{2}})}$
삼중곱을 이용하면 분자와 분모를 $\vec{E_{1}} \times \vec{D}$에 대한 내적으로 구할 수 있음
즉 결정적인 법선 벡터에 대하여 $\vec{T}, \vec{E_{2}}$를 각각 내적하므로 그 비율 $\beta$를 구할 수 있음

t

$t = \frac{\vec{E_{2}} \cdot (\vec{T} \times \vec{E_1})}{\vec{E_{1}} \cdot (\vec{D} \times \vec{E_{2}})}$
삼중곱을 이용하면 $\vec{E_{1}} \times \vec{E_{2}}$의 형식으로 정리할 수 있고 즉 이는 삼각형의 법선 $\vec{S}$에 대한 $\vec{T}, \vec{D}$의 내적인데, 이 때 $\vec{D}$의 크기는 1이므로 간단하게 t가 계산된다