01.31

Collision Detection

Ray - Ray

매우 얇은 원통으로 가정

Ray - Sphere

직선의 방정식 $\vec{r} = \vec{O} + t\vec{d}$와 원의 방정식을 결합하여 $t$에 대한 2차 방정식 계산
판별식을 통해 해의 개수를 알 수 있고, 근의 공식을 통해 교점의 위치를 알 수 있음

Ray - AABB

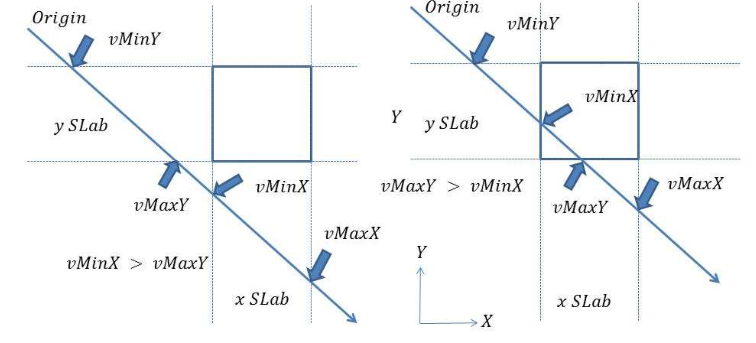
AABB의 각 축에 대하여 Slab을 생성한 후, Ray와 Slab사이의 교점 계산
축 별로 Slab 쌍을 지을 수 있는데, 각 쌍별로 Origin과 가까운 Slab의 교점을 Min, Origin과 먼 교점을 Max로 설정
Min Slab Intersection 중 가장 길이가 큰 maxMin 검색
Max Slab Intersection 중 가장 길이가 작은 minMax 검색
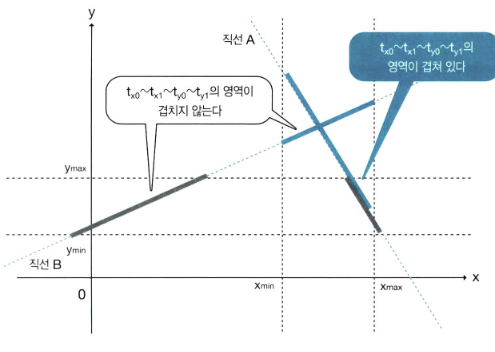
minMax > maxMin 이라면 충돌 판정
교점은 minMax, maxMin 지점

결국 계수 t에 대하여 겹치는 부분이 존재하는지 점검하는 알고리즘

Reference : https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=ybill&logNo=120103496030

Ray - OBB

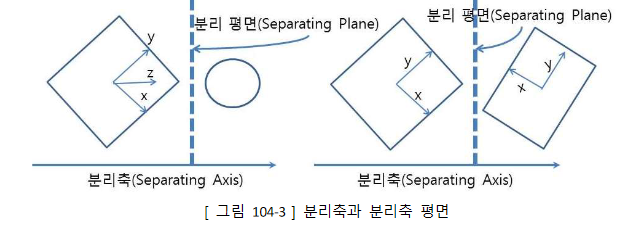
SAT(Separate Axis Theorem)

임의의 축에 대하여 두 물체를 투영했을때 만약 두 물체가 떨어져있다면 두 물체는 충돌하지 않는다
또는 두 물체 사이를 분리할 수 있는 평면이 존재한다

충돌 판정

Real Time Rendering의 경우 Segment - OBB를 제시했는데 이 경우 단순히 정사영된 길이만을 가지고 충돌 여부를 결정할 수 있지만 Ray의 경우 이는 불가능

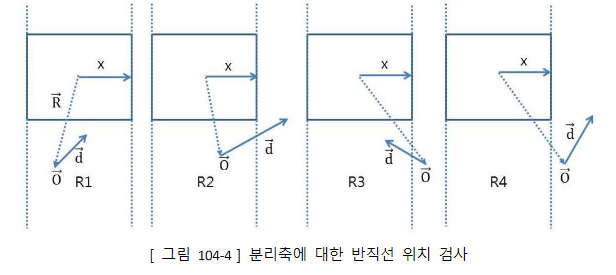
Ray의 경우 총 4가지의 경우에 수가 존재
반직선의 시점이 Object의 안밖 존재여부와 반직선 방향의 Object관통 여부 검사 필요
즉, $\vec{R} = \vec{O} - \vec{C}$, 검사축이 $\vec{A}$일 때,
$\vert\vec{A} \cdot \vec{R}\vert > \vert\vec{A} \cdot \vec{E} \vert$(Ray의 시작점이 Object의 밖에 존재)이고,
$(\vec{E} \cdot \vec{R} \times \vec{E} \cdot \vec{d}) \ge 0$(두 벡터의 방향이 반대)일 경우에만 충돌하지 않는다(R4의 경우만 제외)

충돌 발생

OBB 역시 slab이 회전된 AABB라 가정한다면 direction의 계수 t값을 구할 수 있음