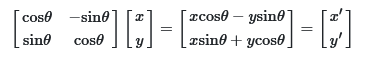09.22

2D 기하변환

이동

기준축 단위로 +- 연산

회전

임의의 회전 θ = 이전에 회전한 각(θ1) + 현재 회전할 각(θ2)
P'(x, y)
= (cos(θ), sin(θ))
= (cos(θ1 + θ2), sin(θ1 + θ2))
삼각함수의 덧셈정리를 적용한 후, cos(θ1) = x, sin(θ1) = y로 정리

삼각함수의 덧셈정리

sin(θ1 + θ2) = sin(θ1)cos(θ2) + cos(θ1)sin(θ2)
cos(θ1 + θ2) = cos(θ1)cos(θ2) - sin(θ1)sin(θ2)

좌표계와 회전변환

전역좌표계의 중심으로부터 떨어진 객체의 회전을 수행하려고 할 경우
좌표 -> 원점 -> 회전 -> 복귀
순서로 수행해야 함.
간단하게 국지좌표계를 기준으로 회전을 수행한 후, 국지좌표계의 원래 위치로 평행이동을 수행하면 됨

신축

기준축에 대하여 */ 연산

반사

기준축에 대하여 * -1 연산

밀림

Qx = Px + k Py (x축 밀림)
Qy = k Px + Py (y축 밀림)

기타 작업 중 발견 사항

Shader

Shader file에서 동일한 Register를 다수의 이름으로 지정한 후, 컴파일 시 E_FAIL을 반환하면서 정상적으로 컴파일되지 않음

// shader
Texture2D g_txTextureA : register(t0);
Texture2D g_txTexMaskA : register(t1);
Texture2D g_txTexMaskA1 : register(t0);

float4 testMask(PS_input input) : SV_TARGET
{
	float4 vMask = g_txTexMaskA1.Sample(g_sampleA, input.t);
	if(vMask.g > 0.9f)
	{
		discard;
	}
	float4 vColor = g_txTextureA.Sample(g_sampleA, input.t);
	return vColor;
}
// cpp
{
	// E_FAIL 반환
    hr = D3DCompileFromFile(path.c_str(), NULL, NULL, entryPoint.c_str(), target.c_str(), 0, 0, &code, &errorCode);
}