AVL 트리

AVL 트리 ?

AVL 트리가 무엇인지 알아보기 전에 알아야 할 것이 있다.
→ 이진 탐색 트리의 단점 : 불균형한 트리 모형을 하고 있을 때 트리의 성능이 O(log n)에서 O(n)으로 떨어진다는 것

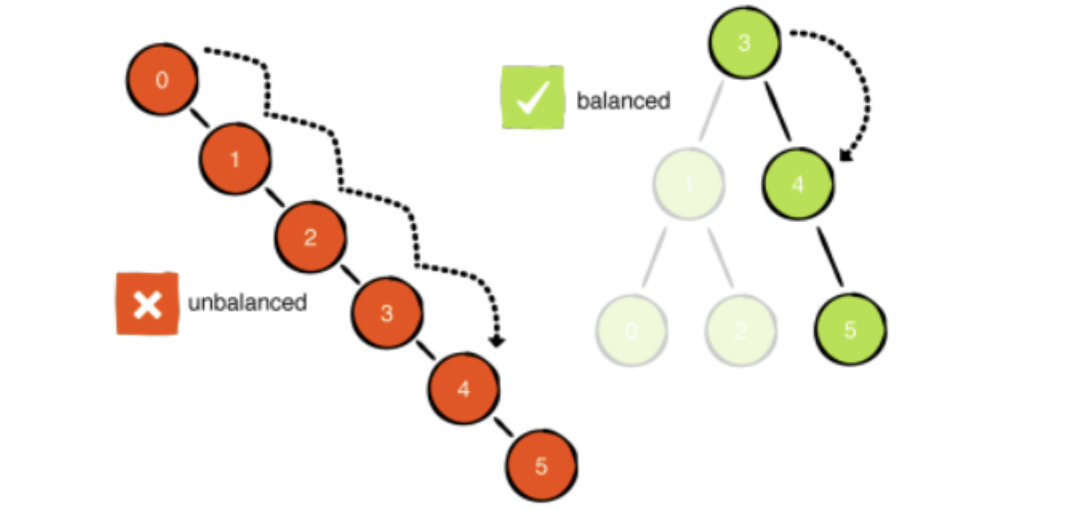
⭐️ AVL 트리는 이러한 문제를 해결하기위해 만들어졌다. 이진트리이면서, 균형을 유지하기 때문에 이진 검색 시 효율성을 보장하게 된다.

✔︎ AVL 트리 특징

• AVL 트리는 이진 탐색 트리의 속성을 가진다.
• 왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1이다.
• 어떤 시점에서 높이 차이가 1보다 커지면 회전(rotation)을 통해 균형을 잡아 높이 차이를 줄인다.
• AVL 트리는 높이를 logN으로 유지하기 때문에 삽입, 검색, 삭제의 시간 복잡도는 O(logN)이다.

균형 트리 (Balanced tree)

트리에는 3가지의 상태가 있다.
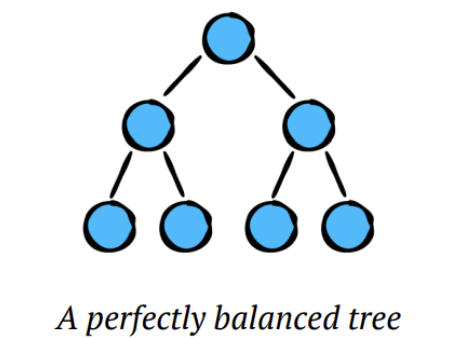
1. 완전 균형 상태 (Perfect Balance)
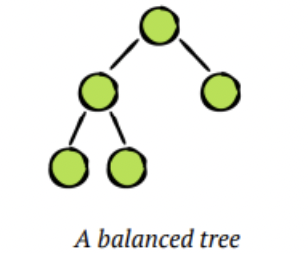
2. 충분한 균형 상태 (Good Enough Balance)
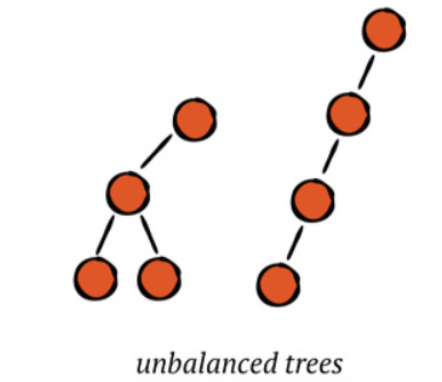
3. 불균형 상태 (Unbalance)

완전 균형 상태 (Perfegt Balance)
✔︎ 모든 레벨에서 노드가 가득 차있는 상태

충분한 균형 상태 (Good Enough Balance)
✔︎ 가장 아래쪽 레벨을 제외하고 모든 노드가 채워져 있는 상태

불균형 상태 (Unbalance)
✔︎ 완전 균형 상태와 충분한 균형 상태의 트리를 제외한 나머지 트리 모양은 불균형한 상태의 트리
→ 성능 저하의 원인
→ 이 문제를 해결하기 위해 AVL Tree를 사용
AVL Tree는 자동으로 균형 잡힌 트리를 제공하기 때문에 탐색, 삽입, 삭제 오퍼레이션들은 O(log n)으로 진행할 수 있게 한다.

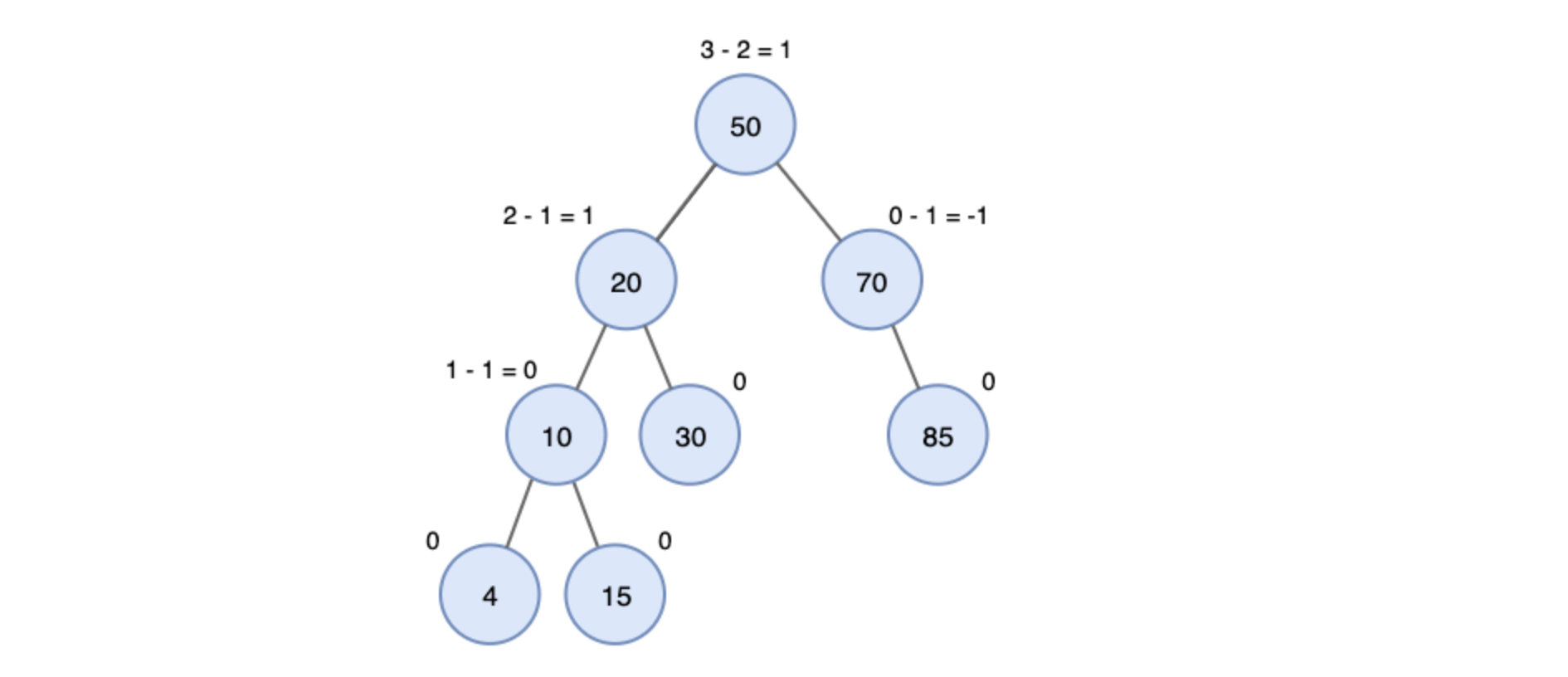
균형 인수(Balance Factor)

⭐️ 왼쪽 서브트리의 높이에서 오른쪽 서브트리의 높이를 뺀 값

• BF가 1이면 왼쪽 서브트리가 오른쪽 서브트리보다 높이가 한단계 높다는 것을 의미한다.
• BF가 0이면 왼쪽 서브트리와 오른쪽 서브트리의 높이가 같다는 것을 의미한다.
• BF가 -1이면 왼쪽 서브트리가 오른쪽 서브트리보다 높이가 한단계 낮다는 것을 의미한다.
• 균형 인수의 절대값이 크면 클수록 트리의 균형이 무너진 상태이다.
  → 균형 인수의 절대값이 2 이상인 경우에 균형을 잡기 위한 재조정을 진행한다.
  
  ✔︎ 위의 ALV 트리를 보면 BF가 -1과 +1 사이에 있음을 알 수 있다.

회전 (Rotation)

이때 우리는 rotation을 활용하여 불균형 트리들을 균형트리로 바꿔준다.

< rotation의 4가지 종류 >
1. Left Left
2. Right Right
3. Left Right
4. Right Left

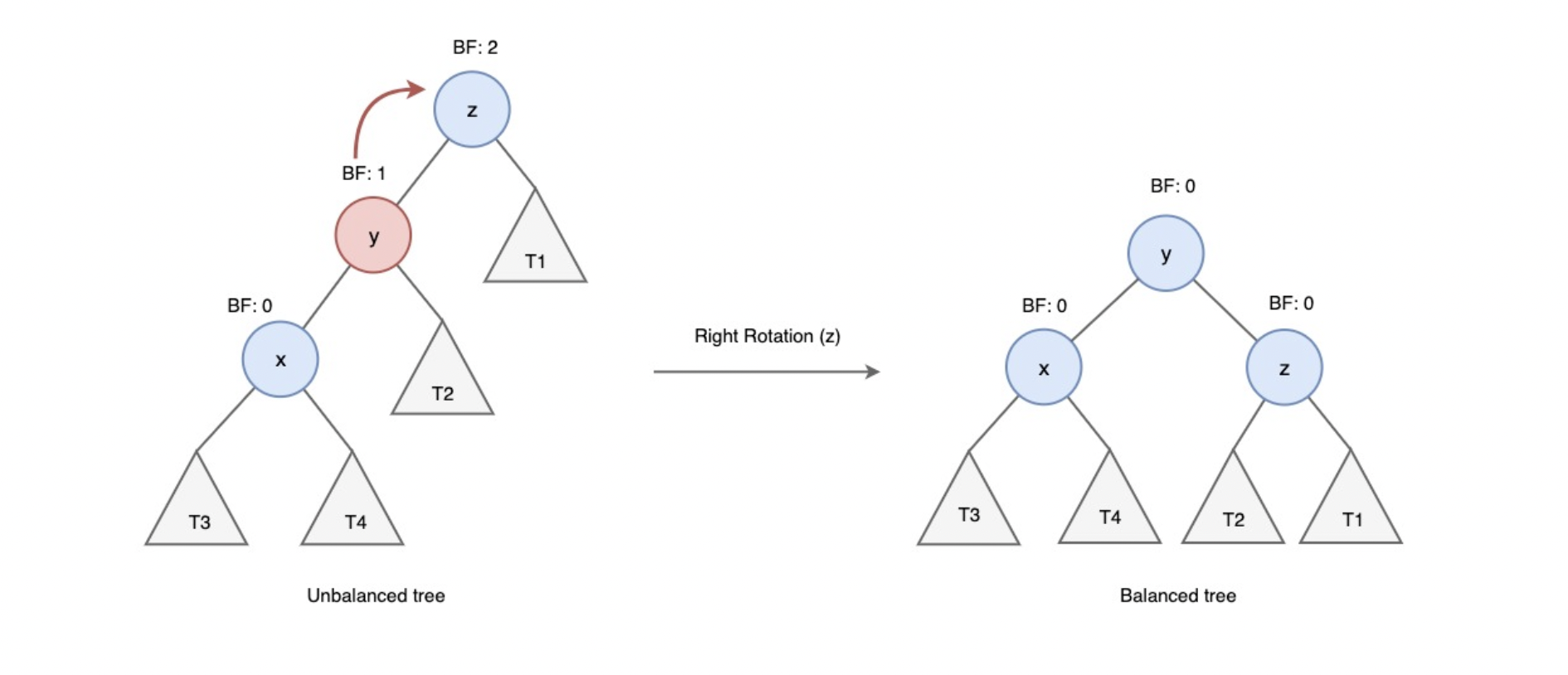
LL( Left Left) case
y는 z의 왼쪽 자식 노드이고, x는 y의 왼쪽 자식 노드인 경우 right rotation을 수행하여 균형을 맞춘다.
< ⭐️ right rotation 수행 과정 >
1. y노드의 오른쪽 자식 노드를 z노드로 변경한다.
2. z노드 왼쪽 자식 노드를 y노드 오른쪽 서브트리(T2)로 변경한다.
3. y는 새로운 루트 노드가 된다.

< 💻 right rotation 구현 >

struct node *rightRotate (struct node *z) {
  struct node *y = z->left;
  struct node *T2 = y->right;
// right 회전 수행
  y->right = z;
  z->left = T2;
// 노드 높이 갱신
  z->height = 1 + max(z->left->height, z->right->height);
  y->height = 1 + max(y->left->height, y->right->height);
// 새로운 루트 노드 y를 반환  
  return y;
}

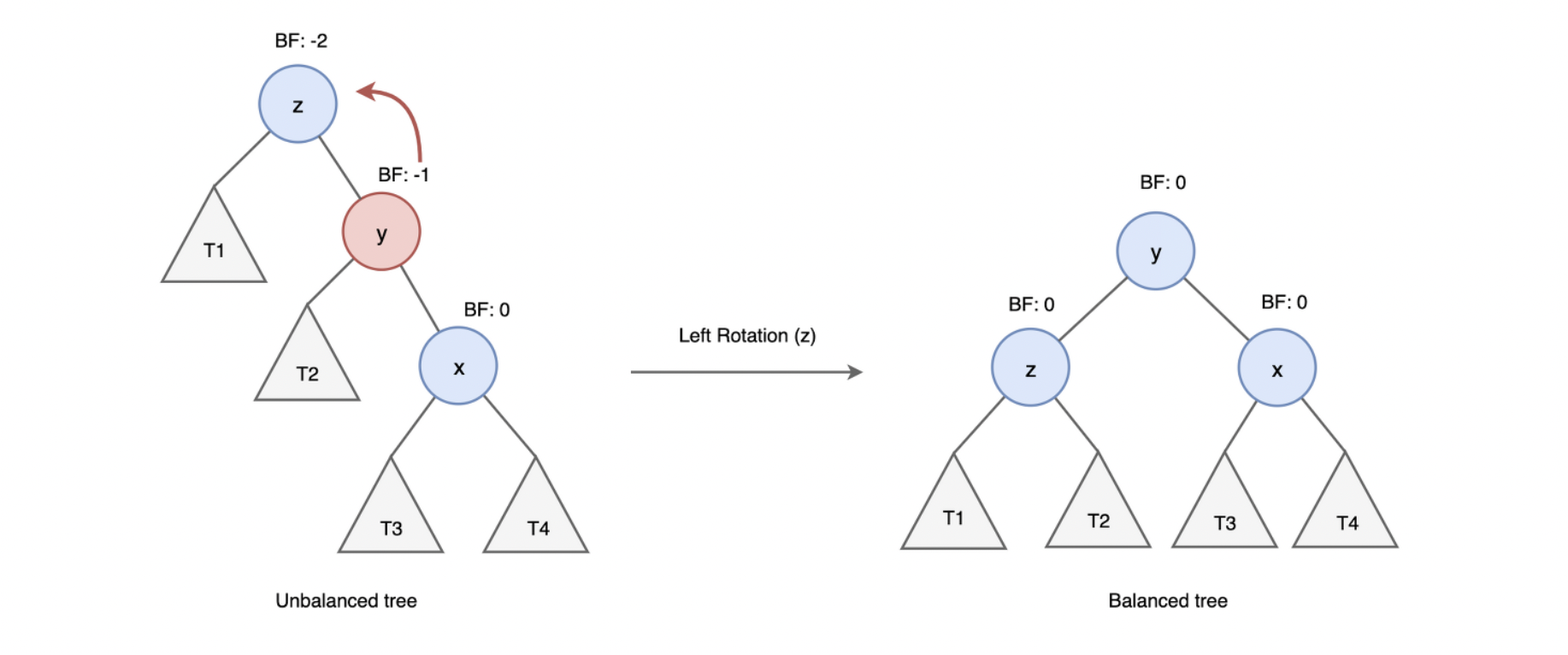
RR (Right Right) case
y는 z의 오른쪽 자식 노드이고, x는 y의 오른쪽 자식 노드인 경우 left rotation을 수행하여 균형을 맞춘다.
< ⭐️ left rotation 수행 과정 >
1. y노드의 왼쪽 자식 노드를 z노드로 변경한다.
2. z노드 오른쪽 자식 노드를 y노드 왼쪽 서브트리(T2)로 변경한다.
3. y는 새로운 루트 노드가 된다.

< 💻 left rotation 구현 >

struct node *leftRotate (struct node *z) {
  struct node *y = z->right;
  struct node *T2 = y->left;
// left 회전 수행
  y->left = z;
  z->right = T2;
// 노드 높이 갱신
  z->height = 1 + max(z->left->height, z->right->height);
  y->height = 1 + max(y->left->height, y->right->height);
// 새로운 루트 노드 y를 반환  
  return y;
}

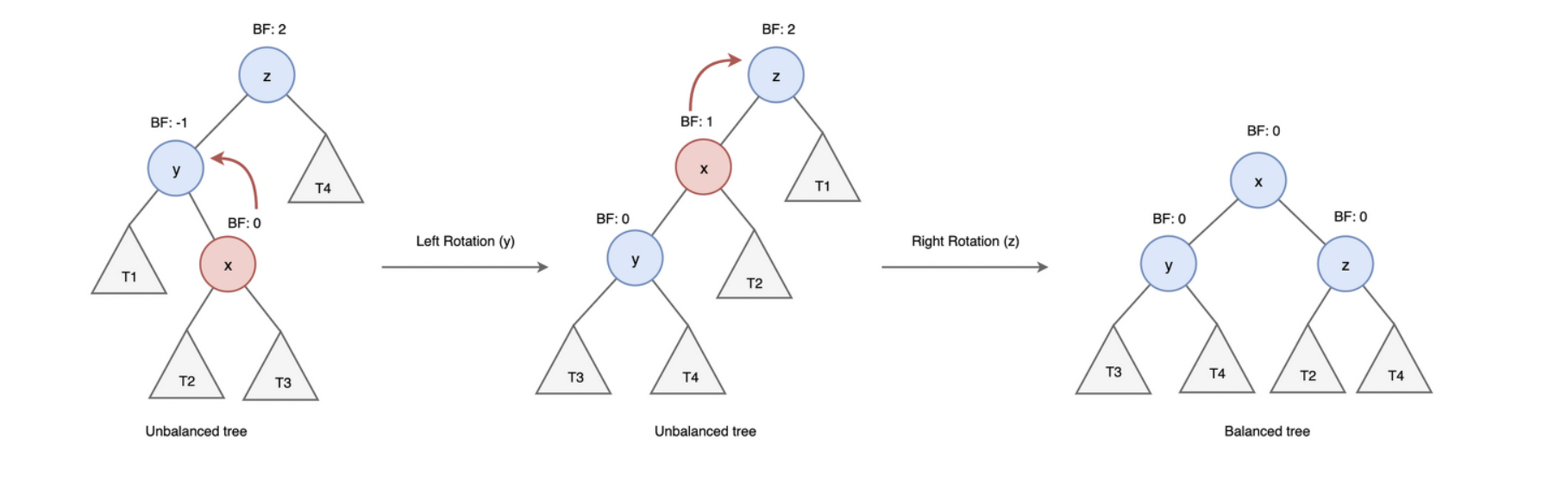
LR (Left Right) case
y는 z의 왼쪽 자식 노드이고, x는 y의 오른쪽 자식 노드인 경우 left , right 순으로 총 두 번의 rotation을 수행하여 균형을 맞춘다.

< 💻 구현 >

y = z->left;
y = leftRotate(y);
z = rightRotate(z);

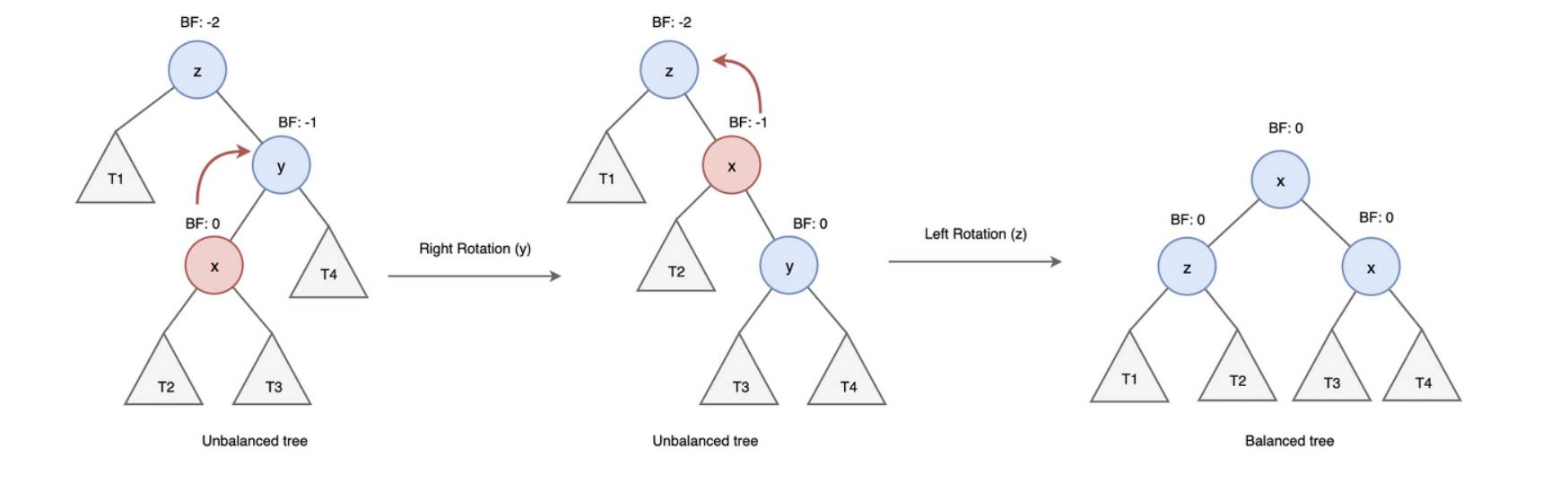
RL (Right Left) case
y는 z의 오른쪽 자식 노드이고, x는 y의 왼쪽 자식 노드인 경우, right, left 순으로 총 두번의 rotation을 수행하여 균형을 맞춘다.

< 💻 구현 >

y = z->right;
y = rightRotate(y);
z = leftRotate(z);

삽입

AVL트리의 삽입 삭제 방식은 이진 탐색 트리와 같다. 하지만 높이 균형을 유지하기 위해 노드의 높이 정보와 case별 rotation 과정이 추가된다.
< 💻 구현 >

struct node {
  int key;
  struct node *left, *right;
  int height;
};

int max(int a, int b) {
  return (a > b)? a : b;
}

struct node* newNode(int key) {
  struct node *temp = (struct *node)malloc(sizeof(struct node));

  temp->data = key;
  temp->left = NULL;
  temp->right = NULL;
  temp->height = 1;
  return temp;
}

struct node *leftRotate (struct node *z) {
  struct node *y = z->right;
  struct node *T2 = y->left;

// left 회전 수행
  y->left = z;
  z->right = T2;

// 노드 높이 갱신
  z->height = 1 + max(z->left->height, z->right->height);
  y->height = 1 + max(y->left->height, y->right->height);

// 새로운 루트 노드 y를 반환  
  return y;
}


struct node *rightRotate (struct node *z) {
  struct node *y = z->left;
  struct node *T2 = y->right;

// right 회전 수행
  y->right = z;
  z->left = T2;

// 노드 높이 갱신
  z->height = 1 + max(z->left->height, z->right->height);
  y->height = 1 + max(y->left->height, y->right->height);

// 새로운 루트 노드 y를 반환  
  return y;
}

// BF(BalanceFactor)값을 가져오는 함수.
int getBalanceFactor(struct node *n) {
  if (n == NULL)
    return 0;
  return n->left->height - n->right->height;
}

// 트리의 높이 균형을 유지하는 함수.
// 4가지 케이스를 가지고 rotate를 수행함.
struct node* rebalance(struct node* root) {
  
  int bFactor = getBalanceFactor(root);
  
  // LL Case
  if (bFactor > 1 && key < node->left->key)
    return rightRotate(root);
  // RR Case
  if (bFactor < -1 && key > node->right->key)
    return leftRotate(root);
  // LR Case
  if (bFactor > 1 && key > node->left->key){
    root->left = leftRotate(root->left);
    return rightRotate(root);
  }
  // RL Case
  if (bFactor < -1 && key < node->right->key){
    root->right = rightRotate(root->right);
    return leftRotate(root);
  }

  return root;
}

// 삽입 함수.
struct node* insert(struct node* root, int key) {

// 삽입 수행
  if (root == NULL)
    return newNode(key);
  if (key > root->data)
    root->right = insert(root->right, key);
  else if (key < root->data)
    root->left = insert(root->left, key);
  else
    return root;

// 노드 높이 갱신
  root->height = 1 + max(node->left->height, node->right->height);

// 노드 균형 유지  
  root = rebalance(root);
  
  return root;
}

✏️ LeetCode 110

class Solution {
private:
    pair<bool,int> isBalancedFast(TreeNode* root){
        if(root == NULL){
            pair<bool , int> p = make_pair(true , 0);
            return p;
        }
        
        pair<bool,int> left = isBalancedFast(root->left);
        pair<bool,int> right = isBalancedFast(root->right);
        
        bool leftAns = left.first;
        bool rightAns = right.first;
        
        bool curr = abs(left.second - right.second) <= 1;
            
        pair<bool,int> ans;
        ans.second = max(left.second , right.second) + 1;
            
        if(leftAns && rightAns && curr){
            ans.first = true;
        }
        else
            ans.first = false;
        
        return ans;
    }
    
public:
    bool isBalanced(TreeNode* root) {
        return isBalancedFast(root).first;
    }
};