탐색 관련 용어
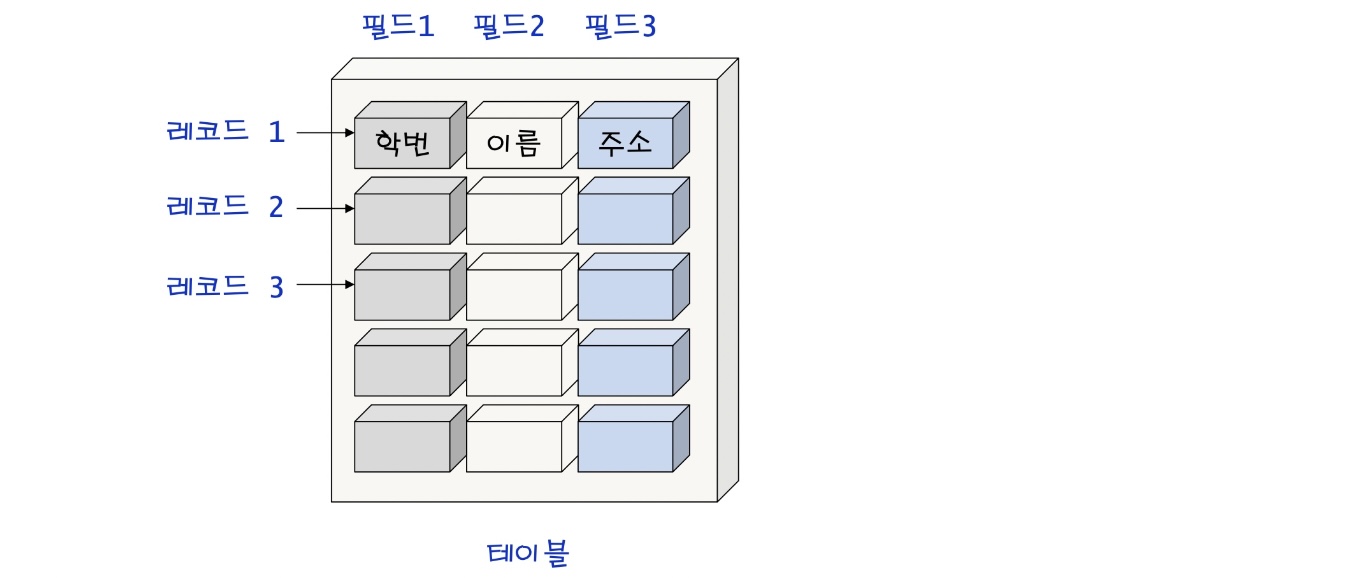
- 레코드 (record)
- 필드 (field)
- 테이블 (table)
- 키 (key)
- 주요키 (primary key)
이진 탐색 트리 ?
✔︎ BST (Binary Search Tree)
✔︎ 이진트리 기반의 탐색을 위한 자료구조로 효율적인 탐색 작업을 위한 자료구조이다.
✔︎ 이진 탐색 트리를 중위 순회 방법으로 순회하면 오름차순으로 정렬된 값을 얻을 수 있다.
✔︎ 다음과 같이 순환적으로 정의된다.
- 모든 노드는 유일한 키를 갖는다.
- 왼쪽 서브트리의 키들은 루트의 키보다 작다.
- 오른쪽 서브트리의 키들은 루트의 키보다 크다.
- 왼쪽과 오른쪽 서브트리도 이진 탐색 트리이다.
이진 탐색 트리의 추상 자료형
데이터 :
이진 탐색 트리(BST)의 특성을 만족하는 이진트리 : 어떤 노드 x의 왼쪽 서브트리의 키들은 x의 키보다 작고, 오른쪽 서브트리의 키들은 x의 키보다 크다. 이때 왼쪽과 오른쪽 서브트리도 모두 이진 탐색 트리이다.
연산 :
• insert(n) : 이진 탐색 트리의 특성을 유지하면서 새로운 노드 n을 이진 탐색 트리에 삽입한다.
• remove(n) : 이진 탐색 트리의 특성을 유지하면서 노드 n을 트리에서 삭제한다.
• search(key) : 키 값이 key인 노드를 찾아 반환한다.
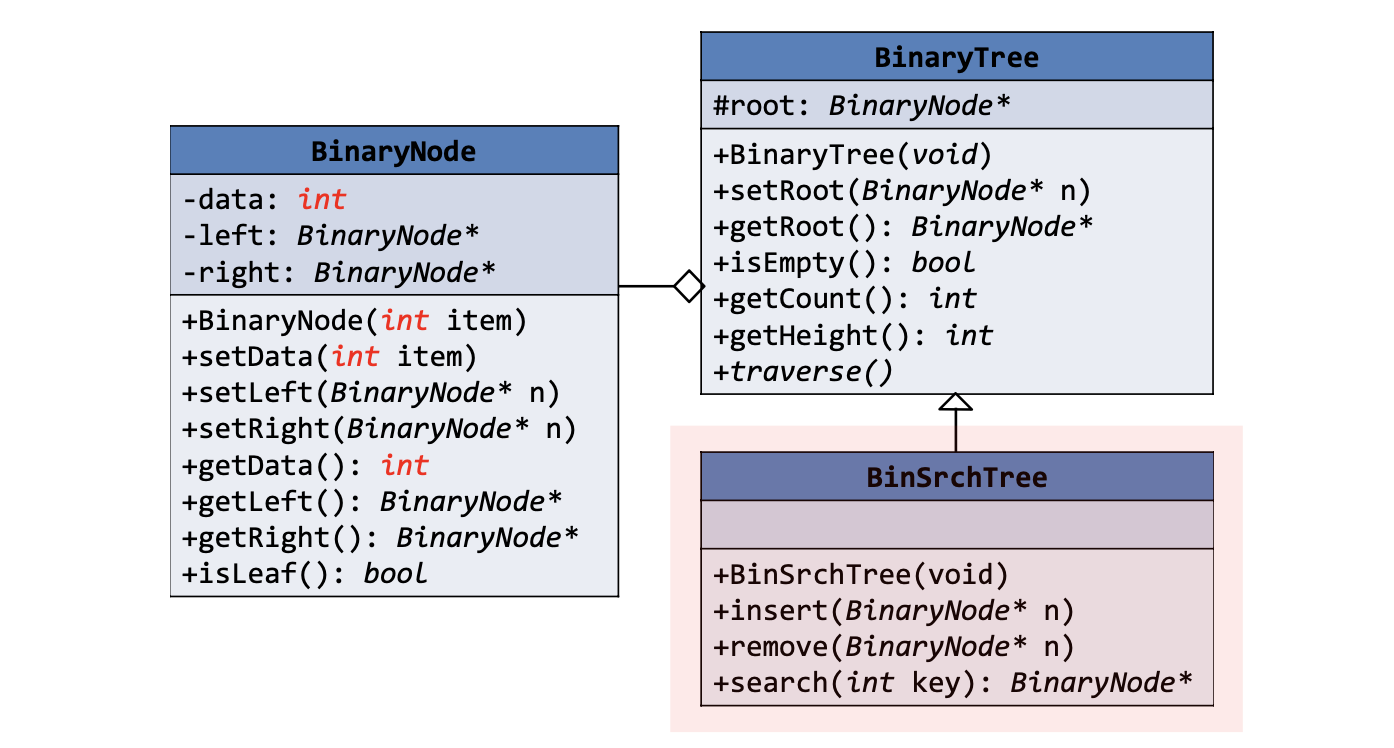
이진 탐색 트리의 클래스 다이어그램
이진 탐색 트리의 탐색 연산
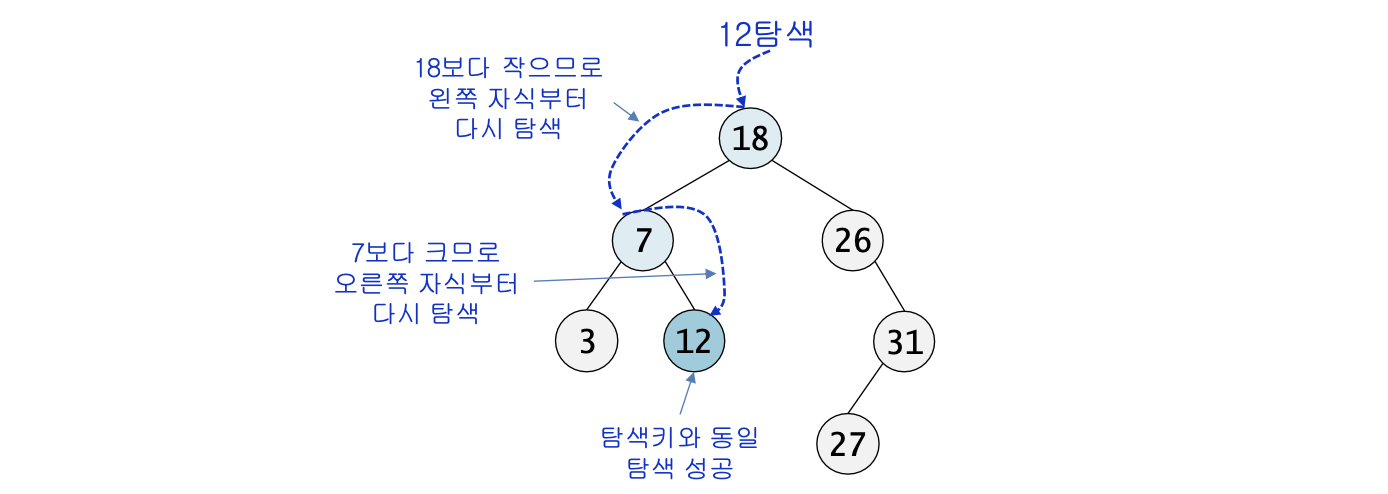
이진 탐색 트리에서 어떤 탐색키를 가진 노드를 찾기 위해서는 먼저 주어진 탐색키와 현재의 루트 노드의 키 값을 비교해야 한다.
- 비교한 결과가 같으면 탐색이 성공적으로 끝난다.
- 비교한 결과 탐색키가 루트 노드의 키 값보다 작으면 탐색은 이 루트 노드의 왼쪽 자식을 기준으로 다시 시작한다.
- 비교한 결과 탐색키가 루트 노드의 키 값보다 크면 탐색은 이 루트 노드의 오른쪽 자식을 기준으로 다시 시작한다.
⭐️ 루트 아래의 노드에서도 같은 과정을 되풀이한다.
1. SearchRecur() : 순환으로 구현한 탐색 함수
💻 C++ 구현
✔︎ 이 함수는 임의의 노드 n을 루트 노드로 하는 트리에서 탐색키 key를 갖는 노드를 찾아 반환한다.// 키 값으로 노드를 탐색하는 함수 (순환적인 방법) // 일반 함수로 구현 (BinSrchTree의 멤버 함수로 넣어도 됨) BinaryNode* searchRecur(BinaryNode *n, int key) { if(n == NULL) return NULL; // n이 NULL if(key == n->getData()) // (1) key == 현재노드의 data return n; else if(key < n->getData()) // (2) key < 현재노드의 data return searchRecur(n->getLeft(), key); else // (3) key > 현재노드의 data return searchRecur(n->getRight(), key); }
2. SearchIter() : 반복으로 구현한 탐색 함수
💻 C++ 구현
✔︎ BinSrchTree 클래스의 멤버로 구현// 키 값으로 노드를 탐색하는 함수 (반복적인 방법) // 일반 함수로 구현 (BinSrchTree의 멤버 함수로 넣어도 됨) BinaryNode* searchIter(BinaryNode *n, int key) { while(n != NULL) { if(key == n->getData()) // (1) key == 현재노드의 data return n; else if(key < n->getData()) // (2) key < 현재노드의 data n = n->getLeft(); else // (3) key > 현재노드의 data n = n->getRight(); } return NULL; // 탐색에 실패한 경우 NULL 반환 }
3. BinaryNode::search() : 노드 클래스에서 순환으로 구현
💻 C++ 구현
✔︎ BinaryNode 클래스의 멤버로 구현
✔︎ 트리의 각 노드들은 모두 자신을 루트로 갖는 서브트리를 대표한다고 생각할 수 있다.// 키 값으로 노드를 탐색하는 함수 (순환적인 방법) // 노드 클래스의 멤버로 구현 (일반 함수가 아님) BinaryNode* BinaryNode::search(int key) { if(key == data) // (1) key == 현재노드의 data return this; else if(key < data && left != NULL) // (2) key < 현재노드의 data return left->search(key); else if(key > data && right != NULL) // (3) key > 현재노드의 data return right->search(key); else // 찾는 노드 없음 return NULL; }
이진 탐색 트리의 삽입 연산
이진 탐색 트리에 원소를 삽입하기 위해서는 먼저 탐색을 수행하는 것이 필요하다.
→ 이진 탐색 트리에서는 같은 키 값을 갖는 노드가 없어야 하기 때문
→ 탐색에 실패한 위치가 바로 새로운 노드를 삽입하느 위치가 되기 때문
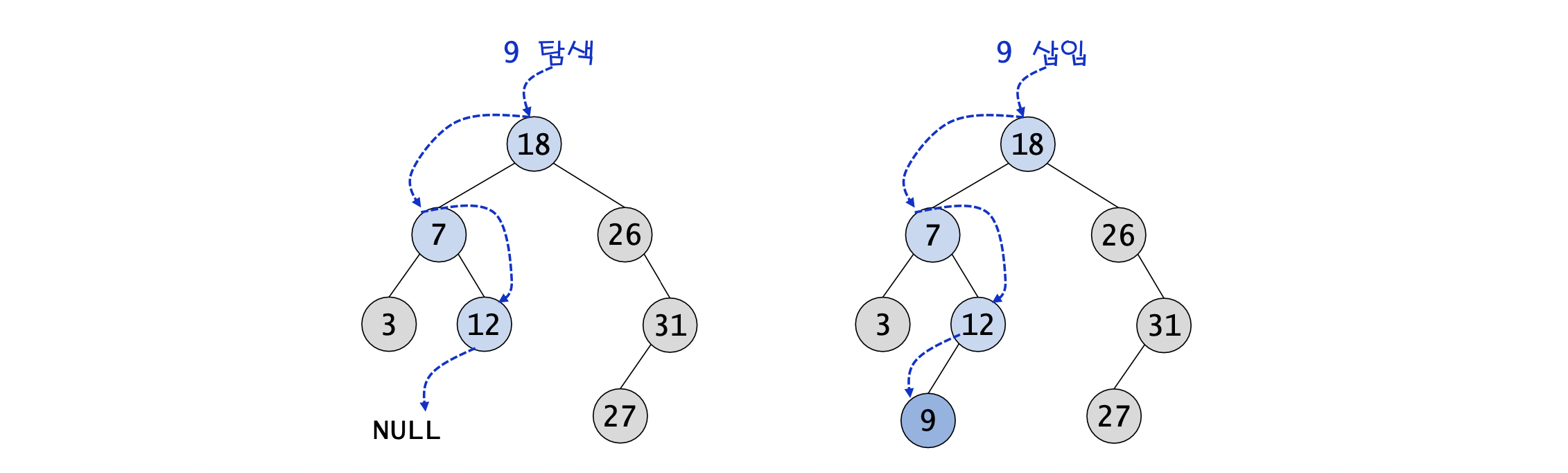
⭐️ 이진 탐색 트리에 노드9를 삽입하는 과정
루트에서부터 9를 탐색해본다.
- 만약 탐색이 성공하면 이미9가 트리 안에 존재하는 것이고, 키가 중복되므로 삽입 불가능하다.
- 만약 9가 트리 안에 없으면 어디선가 탐색이 실패로 끝날 것이다.
바로 실패로 끝난 위치가 9가 있어야 할 곳이다.
→ 따라서 탐색이 실패로 끝난 위치인 12의 왼쪽에 9를 삽입하면 된다.
💻 C++ 구현
// 이진 탐색 트리의 삽입 함수 (순환적인 방법) // 일반 함수로 구현 (BinsrcTree의 멤버 함수로 넣어도 됨) void insertRecur( BinaryNode* r, BinaryNode* n ) { if( n->getData() == r->getData() ) return; else if( n->getData() < r->getData() ) { if( r->getLeft() == NULL ) r->setLeft(n); else insertRecur( r->getLeft(), n ); } else { if( r->getRight() == NULL ) r->setRight(n); else insertRecur( r->getRight(), n ); } }
이진 탐색 트리의 삭제 연산
✔︎ 노드 삭제의 3가지 경우
1. 삭제하려는 노드가 단말 노드일 경우
2. 삭제하려는 노드가 왼쪽이나 오른쪽 서브트리 중 하나만 가지고 있는 경우
3. 삭제하려는 노드가 두 개의 서브트리 모두 가지고 있는 경우
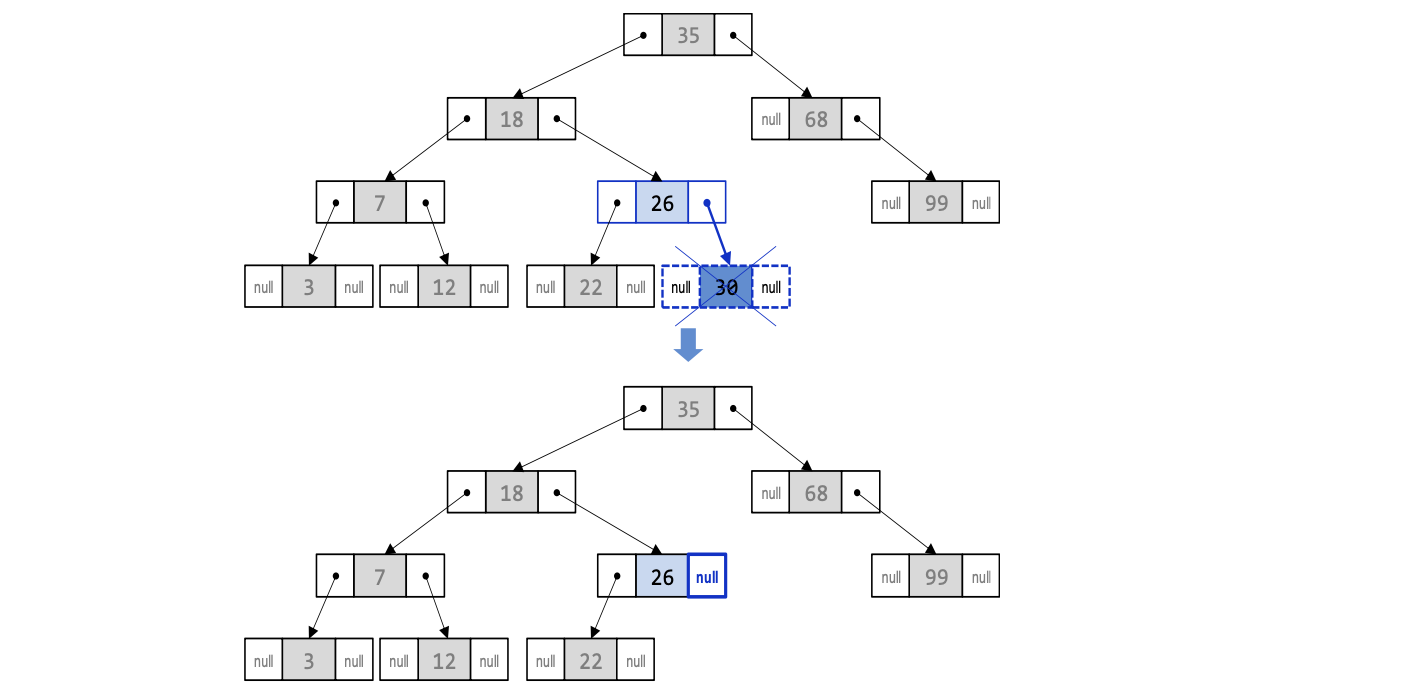
case1 : 삭제하려는 노드가 단말 노드일 경우
단말 노드를 지운다는 것은 단말 노드의 부모 노드를 찾아서 부모 노드의 링크필드를 NULL로 만들어서 연결을 끊으면 된다.
→ 연결 관계가 정리되면 마지막으로 단말 노드를 동적으로 해제시키면 된다.
⭐️ 삭제를 위해 알아야 할 노드 ⭐️
-삭제할 노드 : 30
-삭제할 노드의 부모 : 26
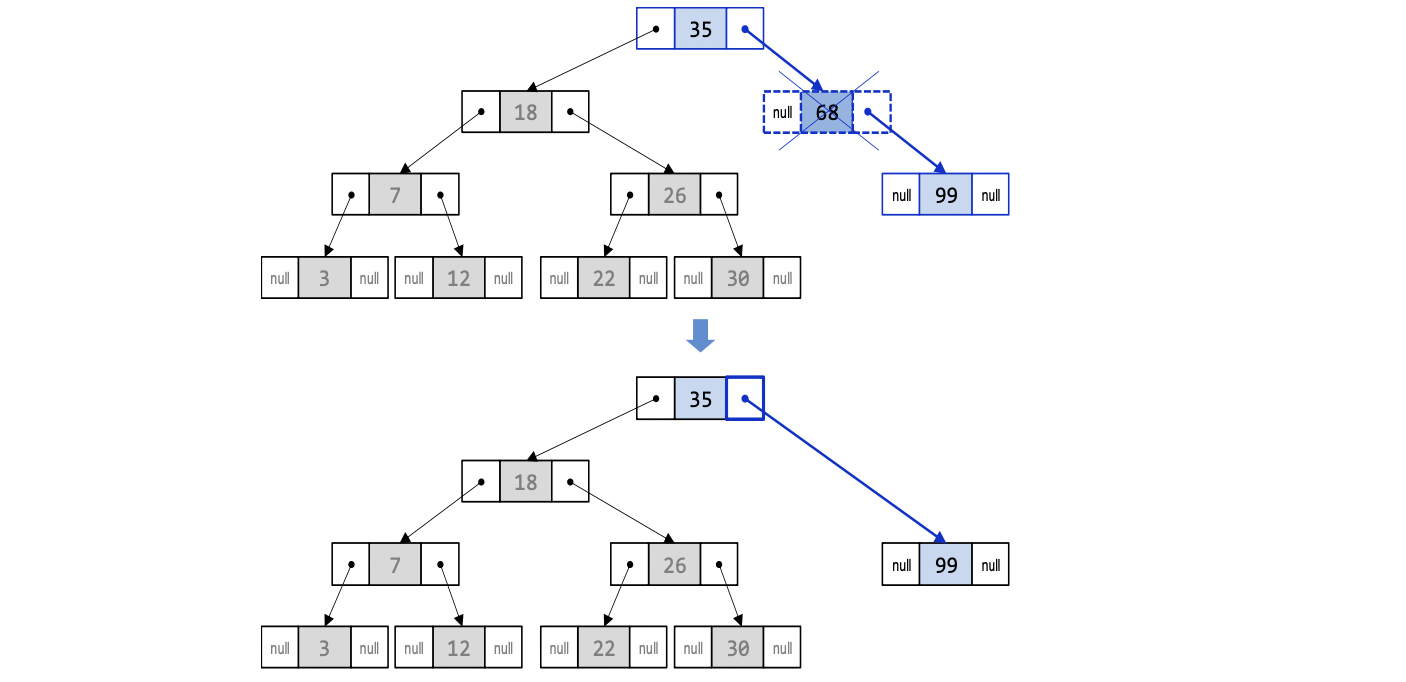
case2 : 삭제하려는 노드가 하나의 서브트리만 가지고 있는 경우
삭제되는 노드가 왼쪽이나 오른쪽 서브트리 중 하나만 가지고 있는 경우에는 그 노드는 삭제하고 삭제된 노드의 유일한 자식을 부모 노드에 붙여주면 된다.
⭐️ 삭제를 위해 알아야 할 노드 ⭐️
-삭제할 노드 : 68
-삭제할 노드의 부모 : 35
-삭제할 노드의 유일한 자식 :99
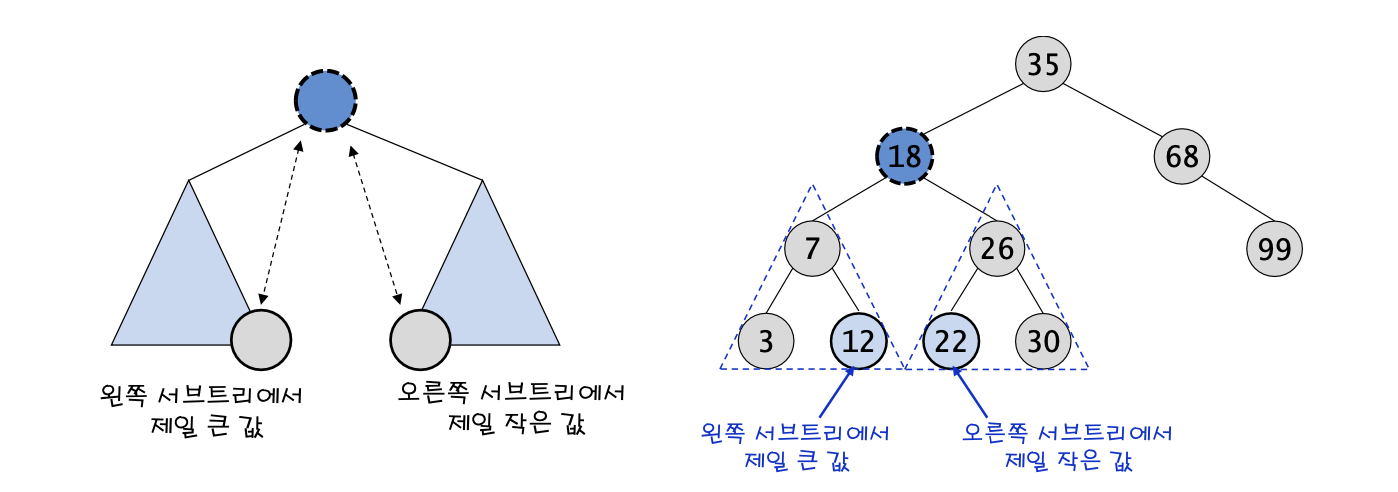
case3 : 삭제하려는 노드가 두 개의 서브트리를 가지고 있는 경우
Q. 어떤 노드를 가져와야 다른 노드들을 변경시키지 않고 이진 탐색 트리의 조건을 계속 만족시킬 수 있을까?
A. "삭제되는 노드와 가장 값이 비슷한 노드" (후계자 노드)
→ 왼쪽 서브트리에서 가장 큰 값 or 오른쪽 서브트리에서 가장 작은 값
→ 왼쪽 서브트리의 가장 오른쪽에 있는 노드 or 오른쪽 서브트리에서 가장 왼쪽에 있는 노드
✲ 후계자 노드 찾는법 ( 여기서는 오른쪽 서브트리에서 가장 작은 값을 후계자로 한다.)
→ 삭제되는 노드의 오른쪽 서브트리에서 가장 작은 값을 갖는 노드는
오른쪽 서브트리에서 왼쪽 자식 링크를 타고 NULL을 만날 때까지 계속 진행하면 된다.
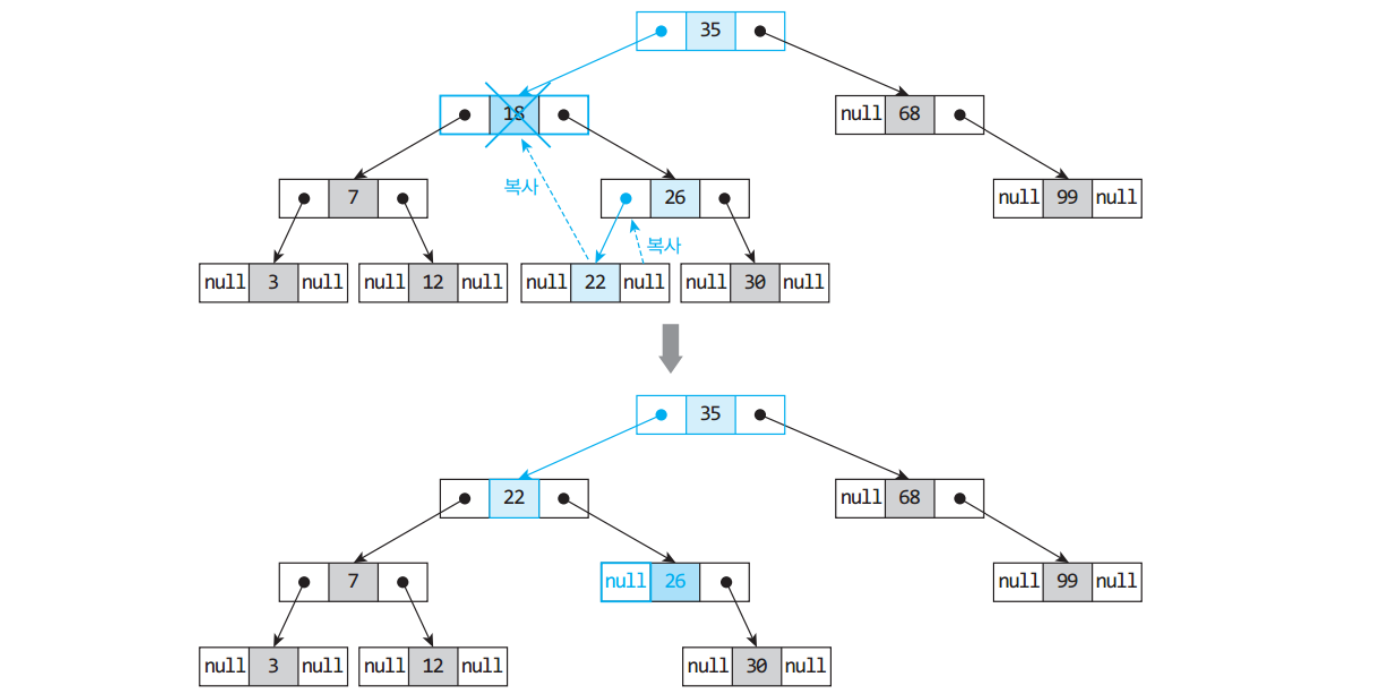
→ 최종적으로 22가 후계자가 되고 22가 18 자리로 이동되게 된다.
⭐️ 삭제를 위해 알아야 할 노드 ⭐️
-삭제할 노드 : 18
-삭제할 노드의 부모 : 35
-후계 노드 : 22
-후계 노드의 부모 : 26
💻 C++ 구현
✔︎ 삭제할 노드 node와 함께 node의 부모 노드의 포인터도 함께 제공해야 한다.// 이진 탐색 트리의 삭제 함수 (순환적인 방법) // 일반 함수로 구현 (BinSrchTree의 멤버 함수로 넣어도 됨) void remove (BinaryNode *parent, BinaryNode *node) { // case 1 : 삭제하려는 노드가 단말 노드일 경우 if( node->isLeaf() ) { if( parent == NULL ) // node == root인 경우 → 공백상태가 됨 root = NULL; else { // 아닌 경우 → parent의 해당 자식을 NULL if( parent->getLeft() == node ) parent->setLeft(NULL); else parent->setRight(NULL); } } // case 2 : 삭제하려는 노드가 왼쪽이나 오른쪽 자식만 갖는 경우 else if( node->getLeft()== NULL|| node->getRight()==NULL ) { // 삭제할 노드의 유일한 자식 노드 → child BinaryNode *child = (node->getLeft() != NULL ) ? node->getLeft() : node->getRight(); // 삭제할 노드가 루트이면 → child가 새로운 root가 됨 if( node == root ) root = child; // 아니면 → 부모 노드의 자식으로 자식 노드 child를 직접 연결 else { if( parent->getLeft() == node ) parent->setLeft(child); else parent->setRight(child); } } // case 3 : 삭제하려는 노드가 두개의 자식이 모두 있는 경우 else { // 삭제하려는 노드의 오른족 서브트리에서 가장 작은 노드를 탐색 // succ → 후계 노드 : 오른쪽 서브트리에서 가장 key가 작은 노드 // succp → 후계 노드의 부모 노드 BinaryNode* succp = node; BinaryNode* succ = node->getRight(); while (succ->getLeft() != NULL) { // 후계 노드 탐색 succp = succ; // 후계 노드의 부모 노드 succ = succ->getLeft(); // 후계 노드 } // 후계 노드의 부모와 후계 노드의 오른쪽 자식을 직접 연결 if( succp->getLeft() == succ ) succp->setLeft(succ->getRight()); else // 후계 노드가 삭제할 노드의 바로 오른쪽 자식인 경우 succp->setRight(succ->getRight()); // 후계 노드 정보를 삭제할 노드에 복사 node->setData(succ->getData()); // 삭제할 노드를 후계 노드로 변경 : 실제로는 후계 노드가 제거됨 node = succ; } delete node; // 메모리 동적 해제 }이 함수는 일반 함수가 아니라 BinSrchTree의 멤버 함수로 구현해야 하며,
삽입이나 탐색 연산과 같이 노드 클래스에서 구현할 수는 없다.
→ 삭제를 위해 여러 노드의 정보가 필요하기 때문
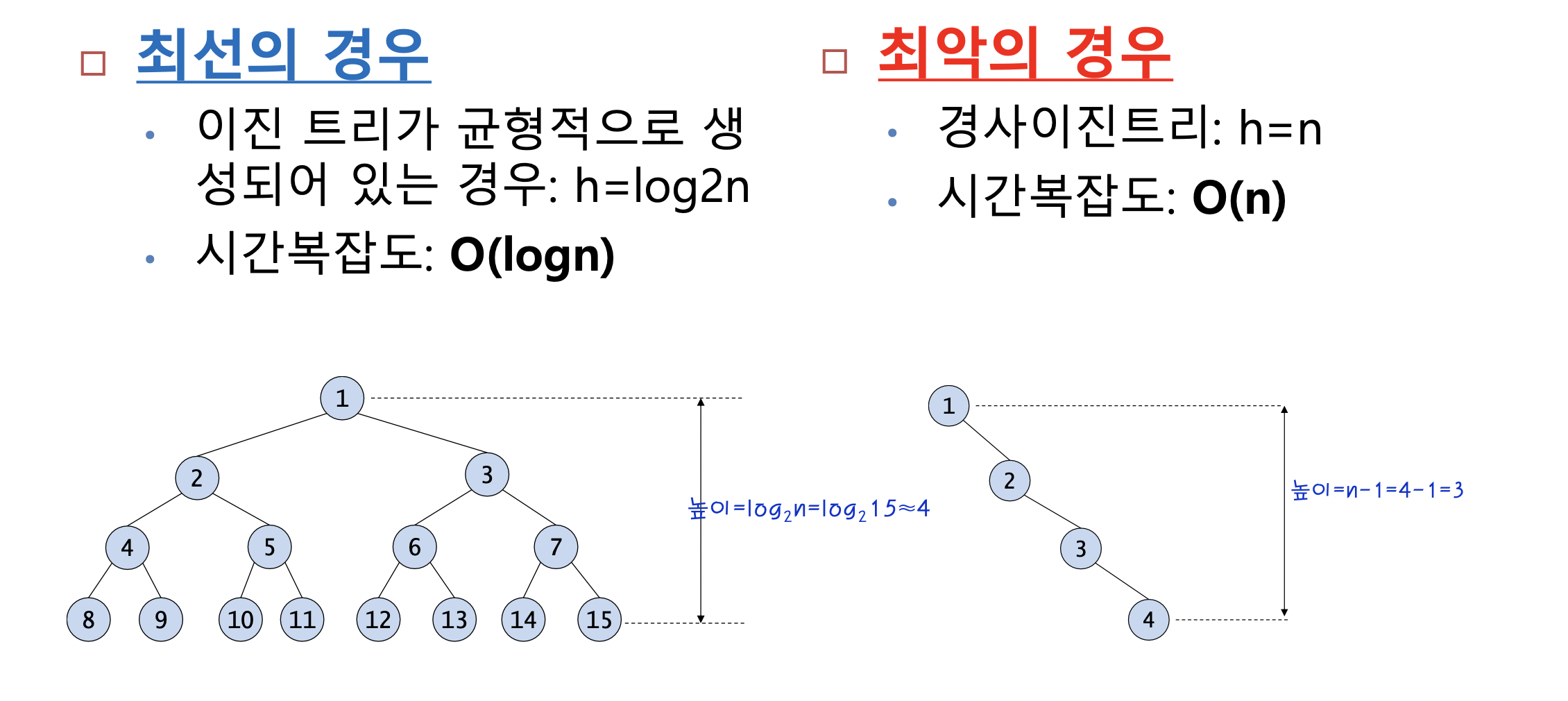
이진 탐색 트리의 성능 분석
이진 탐색 트리에서의 탐색, 삽입, 삭제 연산의 시간 복잡도는 트리의 높이를 h라고 했을 때 O(h)가 된다. (높이 h에 비례)
✏️ LeetCode 98
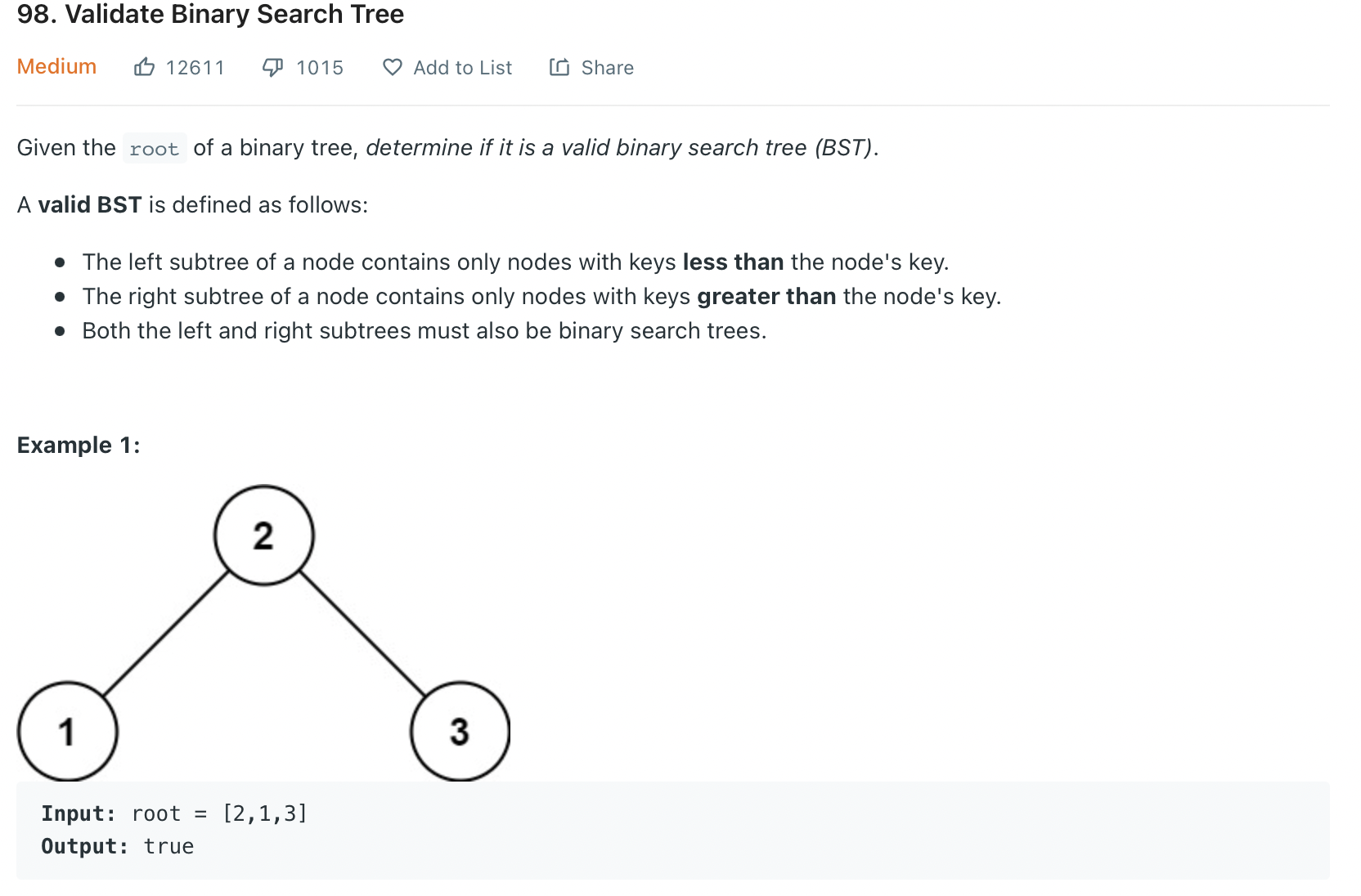
class Solution {
public:
bool validate(TreeNode* root, TreeNode* low, TreeNode* high) {
// Empty trees are valid BSTs.
if (root == nullptr) {
return true;
}
// The current node's value must be between low and high.
if ((low != nullptr and root->val <= low->val) or
(high != nullptr and root->val >= high->val)) {
return false;
}
// The left and right subtree must also be valid.
return validate(root->right, root, high) and
validate(root->left, low, root);
}
bool isValidBST(TreeNode* root) {
return validate(root, nullptr, nullptr);
}
};✏️ LeetCode 99

class Solution {
TreeNode*first;
TreeNode*prev;
TreeNode*mid;
TreeNode* last;
void inorder(TreeNode*root)
{
if(root==NULL)
{
return;
}
inorder(root->left);
if(prev!=NULL && (root->val<prev->val))
{
if(first==NULL)
{
first=prev;
mid=root;
}
else
{
last=root;
}
}
prev=root;
inorder(root->right);
}
public:
void recoverTree(TreeNode* root) {
first=mid=last=NULL;
prev=new TreeNode(INT_MIN);
inorder(root);
if(first&& last)
{
swap(first->val,last->val);
}
else if(first && mid)
{
swap(first->val,mid->val);
}
}
};✏️ LeetCode 700
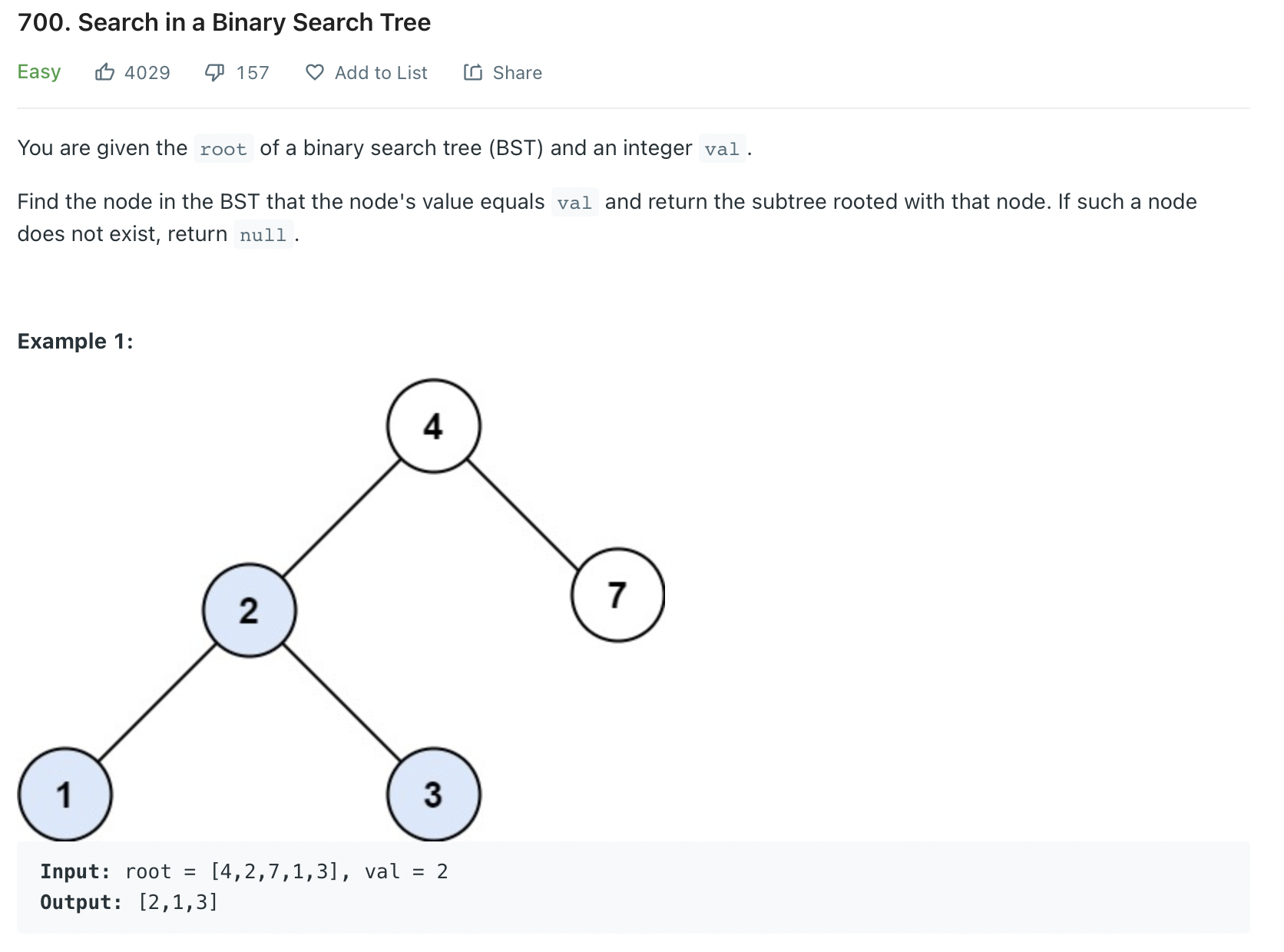
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if(root==NULL){
return root;
}
if(root->val> val){
root=searchBST(root->left,val);
}
else if(root->val < val){
root=searchBST(root->right,val);
}
return root;
}
};✏️ LeetCode 701
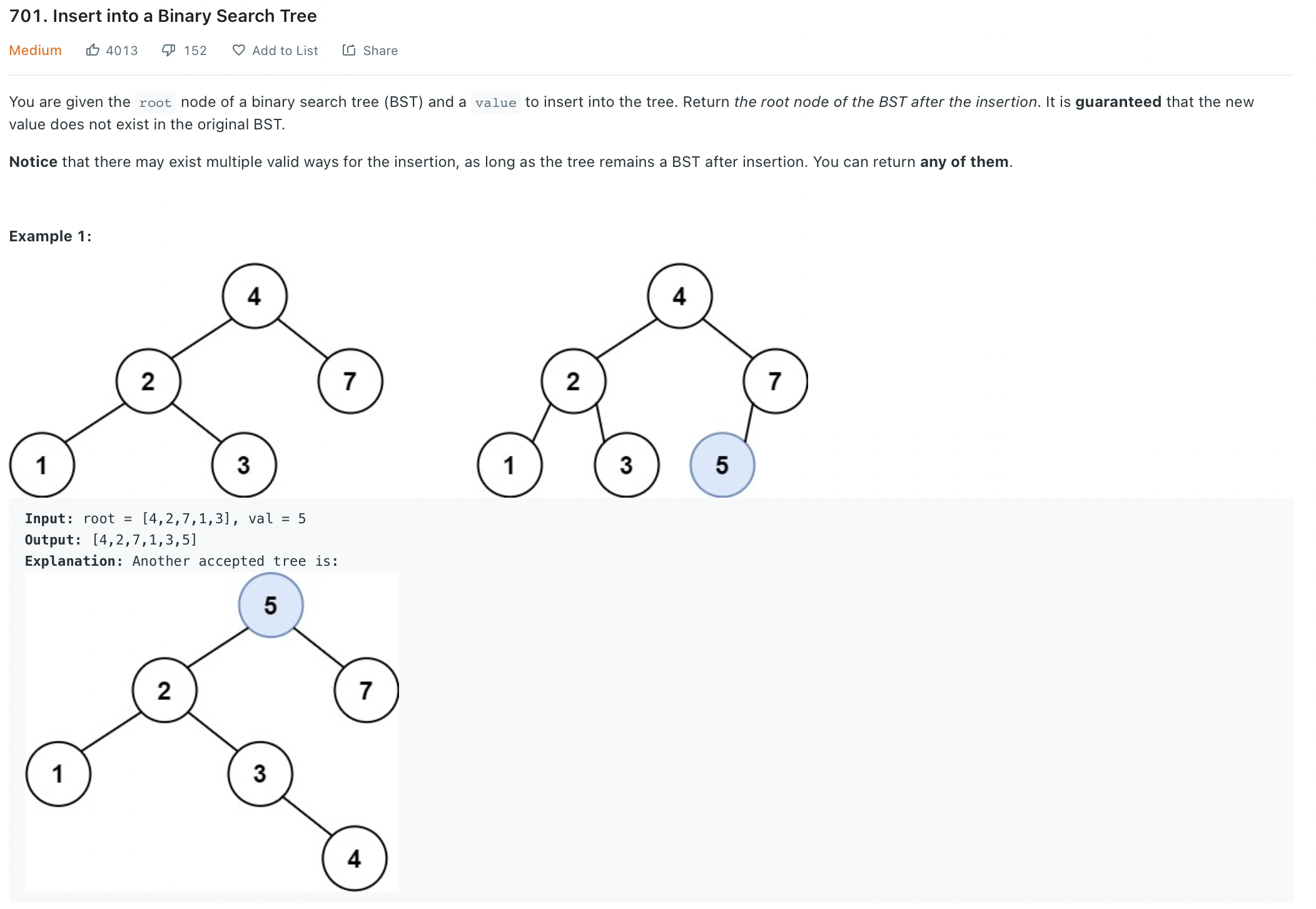
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(root == NULL) {
TreeNode* n = new TreeNode(val);
root = n;
return root;
}
helper(root, val);
return root;
}
void helper(TreeNode* root, int val) {
if(root->left == NULL && root->val > val) {
TreeNode* n = new TreeNode(val);
root->left = n;
return;
}
if(root->right == NULL && root->val < val) {
TreeNode* n = new TreeNode(val);
root->right = n;
return;
}
if(root->val > val) {
helper(root->left, val);
}
else {
helper(root->right, val);
}
}
};