벨만포드 알고리즘?
• 한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘
• 시간복잡도 O(VE) V: 정점 수, E: 간선 수
• 다익스트라 알고리즘이 모든 가중치가 양수인 경우에만 사용할 수 있는 반면, 벨만-포드 알고리즘은 노드 간의 간선 가중치가 음수인 경우에도 사용할 수 있다.
✲ 다만 시간 복잡도는 벨만-포드가 더 크기 때문에 가중치가 모두 양수라면 굳이 벨만-포드를 사용할 필요 없다.
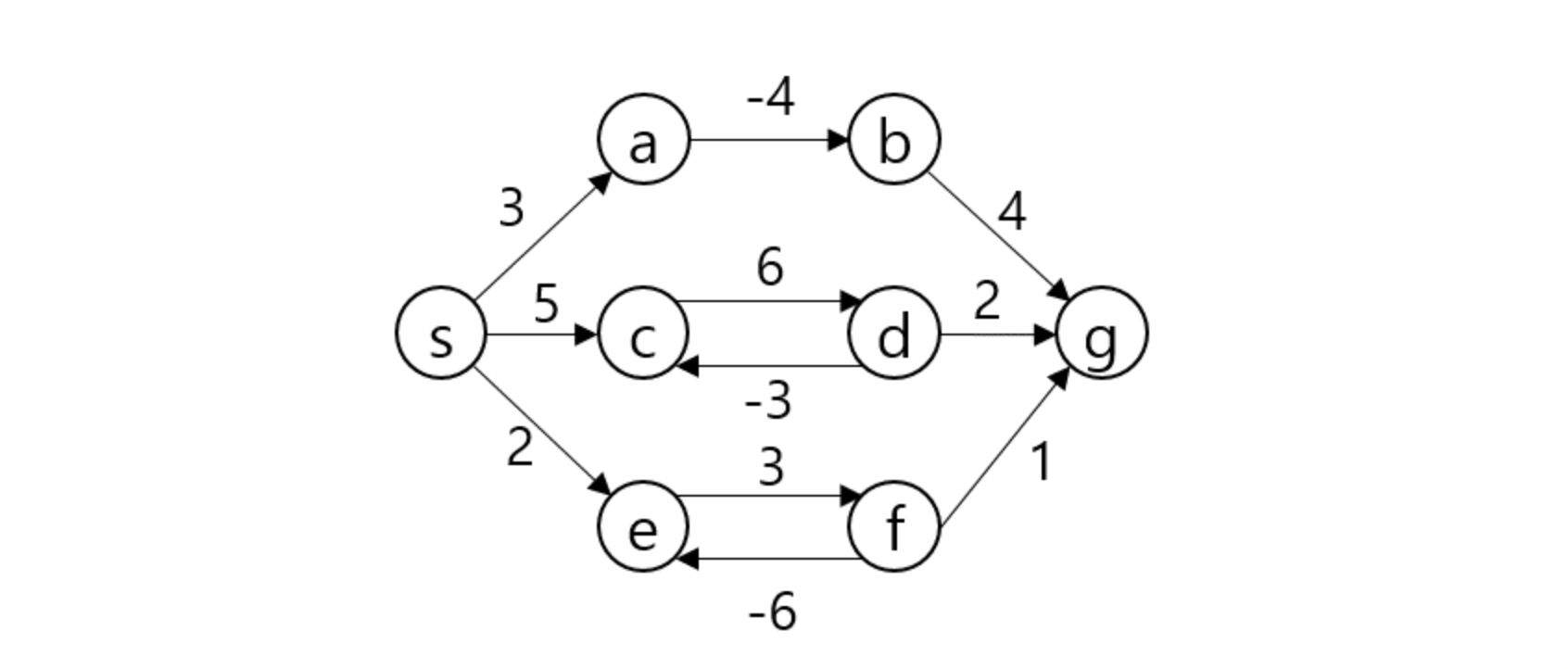
음수 사이클이 문제가 되는 이유
단순 음수 간선일 경우 : 단순 경로이므로 그대로 가중치를 계산하면 된다.
사이클이 존재하나 양수값이 더 클 경우 : 사이클을 순환하여도 이득이 없으므로 그대로 진행한다.
사이클이 존재하고 음수값이 더 클 경우 : 사이클을 순환할 수록 가중치가 감소해 최소 비용을 찾는 입장에서 사이클을 무한히 순환하고 목적지에 도착함은 실질적인 최단 경로라 보기 어렵다. 적어도 동일 노드를 방문하면 안된다는 등 제약 조건이 있어야 할 것이다.
⭐️ 최단 거리는 순환되어서는 안된다는 가정을 담고 있으므로 경로(Edge) 길이는
|V|−1 이 된다.
벨만포드 알고리즘이 사이클을 판단하는 방법
다른 알고리즘들의 경우 대부분 if문에서 기존의 경로와 비교를 한 뒤 계속해서 이득이 되는곳을 찾는다. 하지만 벨만-포드는 '노드 to 노드'에 관점을 두기보다 경로 자체를 탐색하게 된다. 그래서 모든 경로를 대상으로 1번 탐색을 하고 이후 한번 더 탐색을 할 때 기존 값에서 줄어드는 값이 있다면 사이클로 판단하게 된다. 한마디로 보는 관점이 다르기 때문에 한번 더 돌릴 수 있는 것이다.
작동 원리
1️⃣ 시작 노드에 대해서 거리를 0으로 초기화, 나머지 노드는 거리를 무한으로 설정
2️⃣ 정점 수(n) -1 만큼 다음 과정을 반복
3️⃣ 매 반복 마다 모든 간선 확인
4️⃣ 현재 간선을 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우, 거리 정보 갱신
5️⃣ n-1번 반복 이후, n번째 반복에서도 거리 값이 갱신된다면 음수 순환이 존재
⭐️ 다익스트라와의 차이점은 매 반복마다 모든 간선을 확인한다는 것
(다익스트라는 방문하지 않는 노드 중에서 최단 거리가 가장 가까운 노드만을 방문)
예시
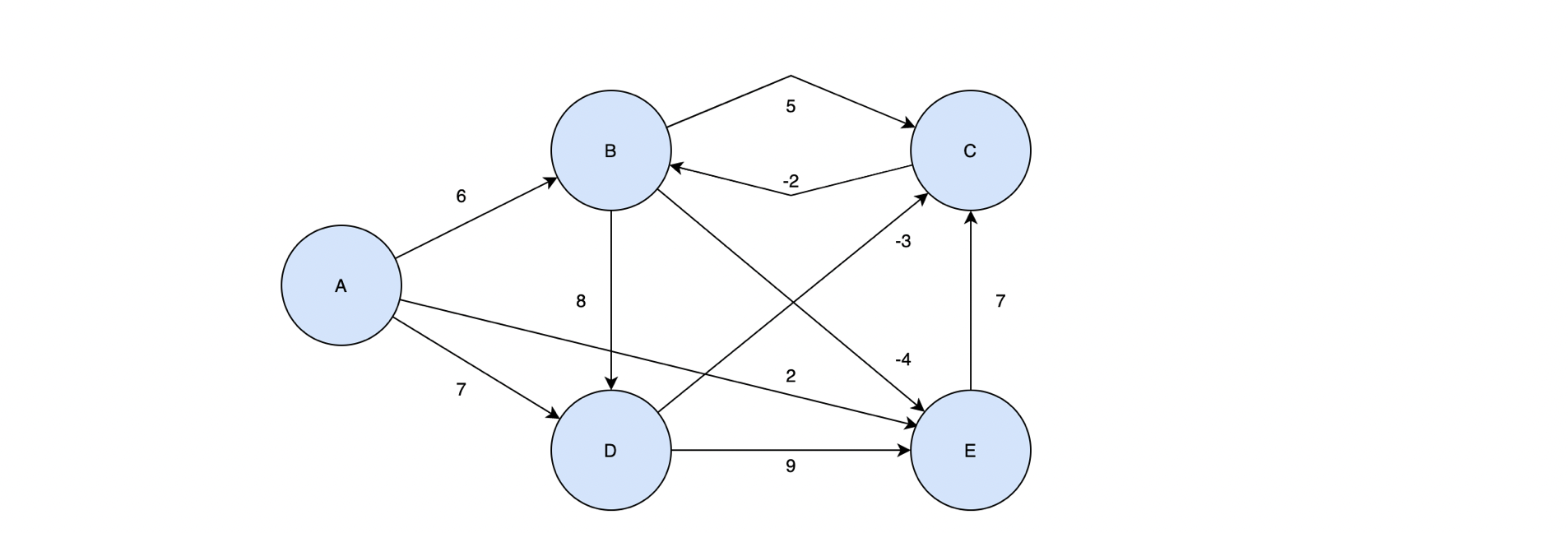
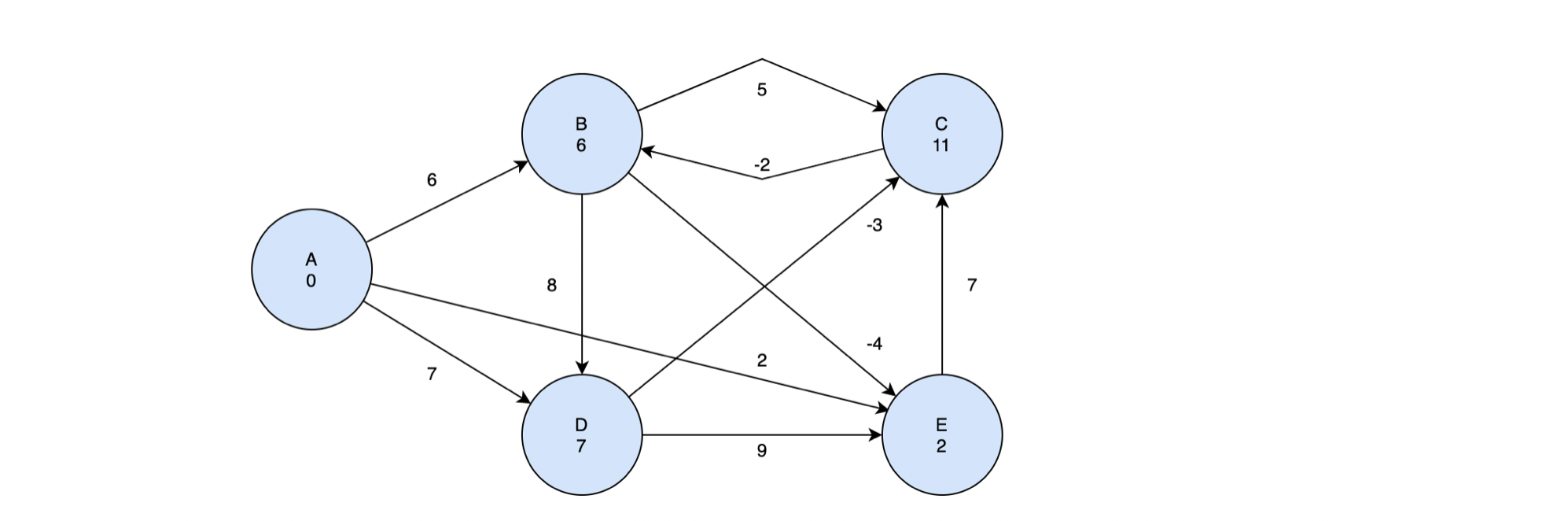
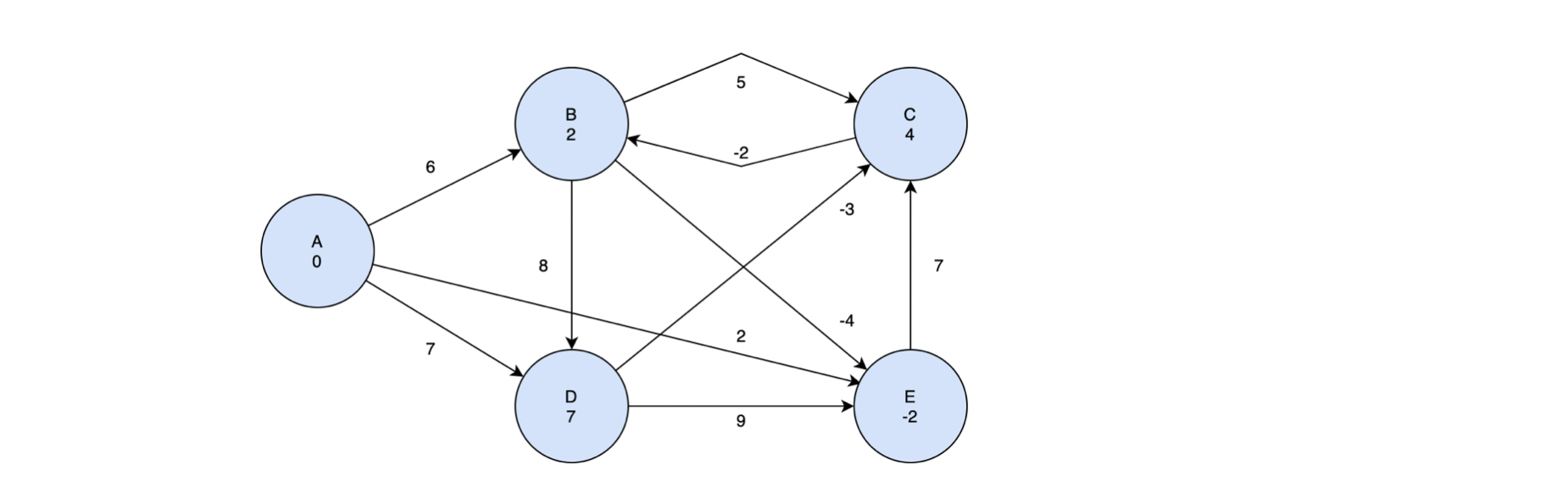
📌 위 그래프를 예시로 벨만포드 알고리즘을 적용해보자.
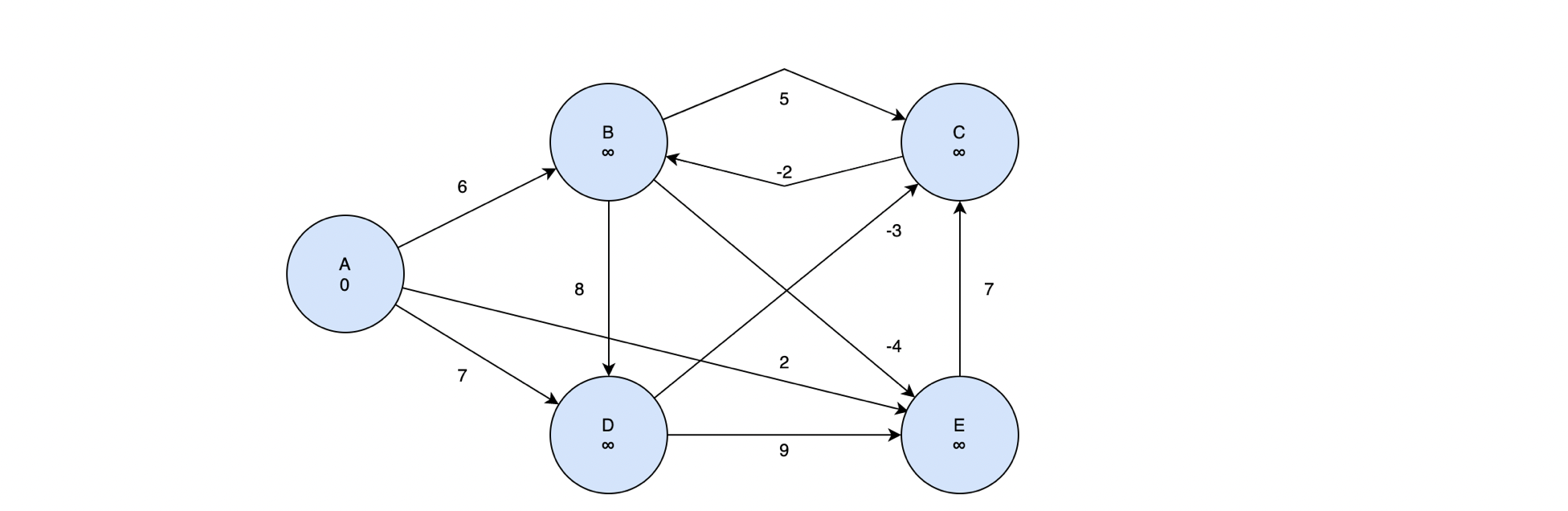
먼저 시작정점을 정하고 각 정점들의 값을 초기화 해주어야 한다. 이 예시에서는 시작점을 A로 정하겠다. 그리고 A만 길이 변수를 0으로 초기화 하고 나머지 정점들에 대해서는 양의 무한대를 지정한다.
시작점인 A 정점으로부터 연결되어 있는 노드들에 대해 Relaxtion 을 진행한다.
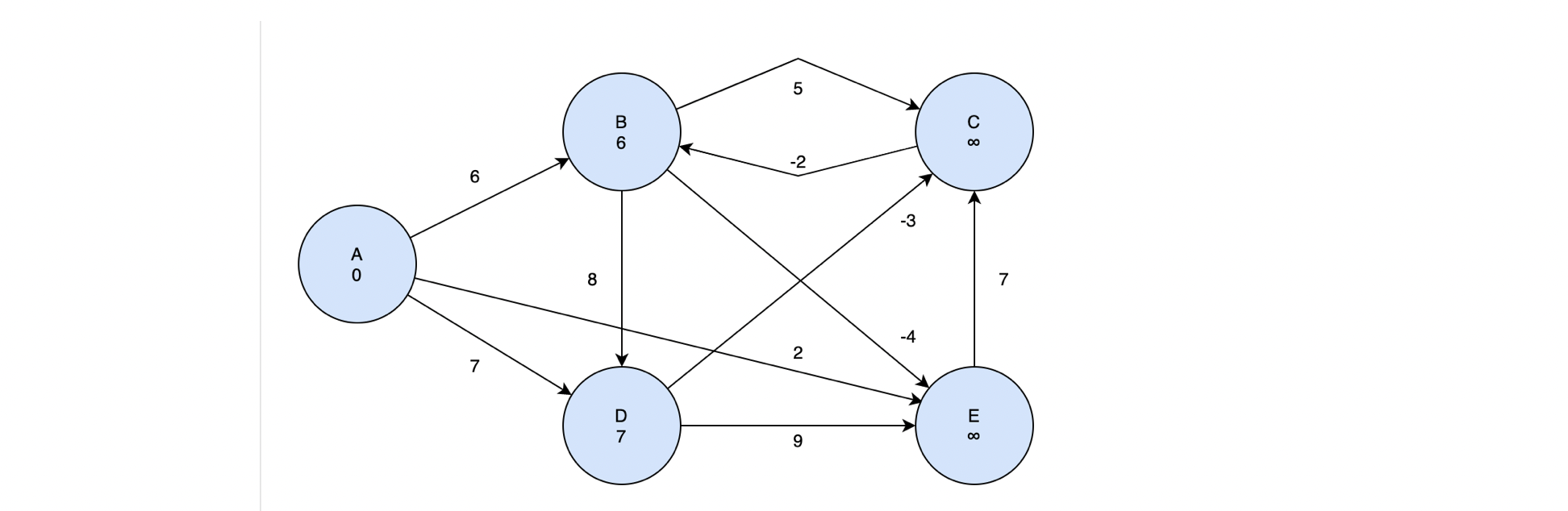
• B 정점에 저장된 최단거리 값은 양의 무한대였는데, A로부터 B까지의 거리인 6이 더 작기 때문에 d[B]는 6이 되고, p[B]는 A가 된다. p[v]는 최단경로에서 정점 v 바로 직전에 나온 정점을 의미한다.
• 같은 맥락으로 A로부터 D까지의 거리를 계산하게 되면 d[D]는 7이 된다.
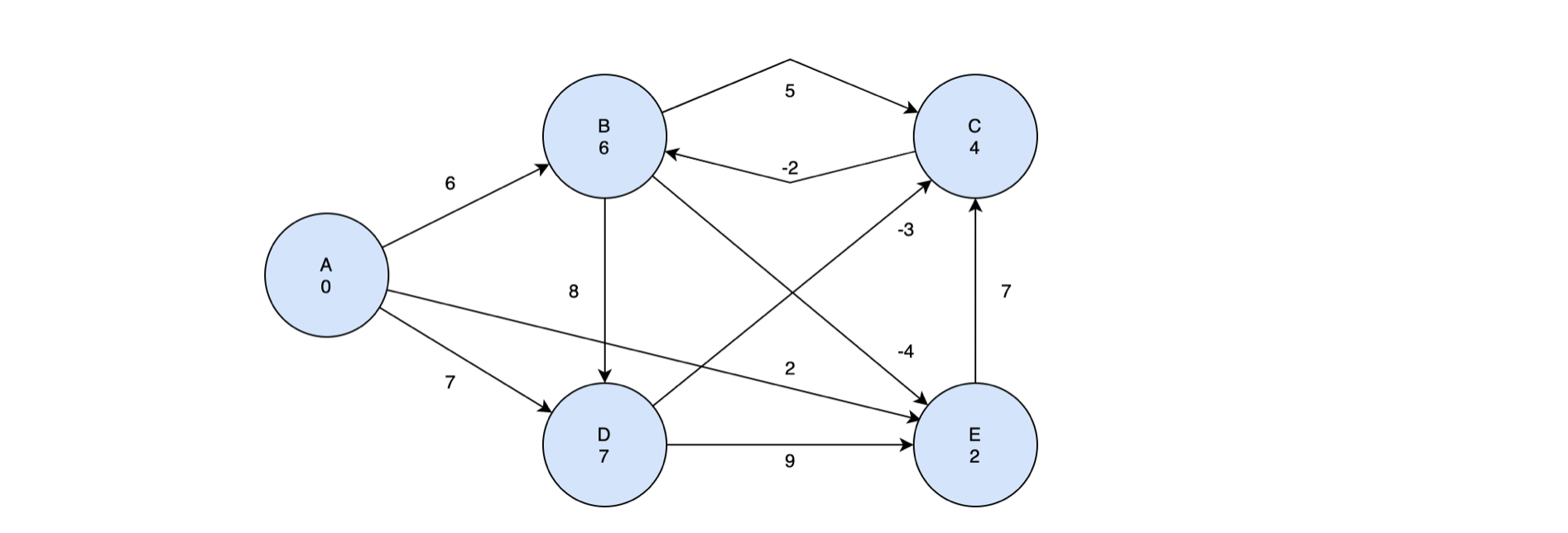
이제 정점 A에 대한 Relaxation 이 끝났으니, 다른 정점들도 모두 Relaxation을 진행해야한다. 다음 정점은 B 정점이다(사실 순서는 상관없다). 우리는 시작점 A로부터 B와 연결된 모든 정점들 까지의 거리를 구하면 된다.
• B와 연결된 C정점까지 도달하기 위해서는 A에서 B까지의 최단 거리인 6에 B에서 C로 이동하는 최단거리를 더해주면 된다. 현 시점에서 C까지 도달하는 최단거리는 양의 무한대로 설정되어 있으므로 간선 BC를 통해 연결되는 것이 가장 작을 수 밖에 없다. 따라서 d[C]는 6+5 인 11이 된다.
• B와 연결된 정점 E에 도달하는 최단거리 역시 위와 같은 과정을 통해 6-2로 4가 되는 것을 알 수 있다.
• B와 연결된 마지막 정점 D에 도달하기 위해서는 거리 AB와 거리 BD를 더해주어야 한다. 그럼 거리가 6+8=14가 되는데, 이 거리는 A에서 곧바로 D로 이동하는 거리보다 크다. 우리는 최단거리를 유지해야하기 때문에 D까지의 최단거리는 A에서 곧장 이동하는 7로 유지한다.
이제 정점 D에 대한 Relaxation을 진행해보자. 정점 D는 C와 E로 연결된다.
• 정점 D를 거쳐서 C로 이동하게 되면 총 거리가 7 - 3 = 4가 된다. 기존에 C까지의 최단거리는 B를 통해가는 11로 설정되어있었기 때문에 더 짧은 최단거리가 나왔으므로 d[C]를 새로운 값으로 갱신해준다.
• 정점 D를 거쳐서 정점 E로 이동하게 되면 총 거리가 7 + 9 + 11이 된다. 이 거리는 기존에 최단거리였던 정점 B를 거쳐서 E로 이동하는 거리보다 작기 때문에 새로 갱신하지 않고 넘어간다.
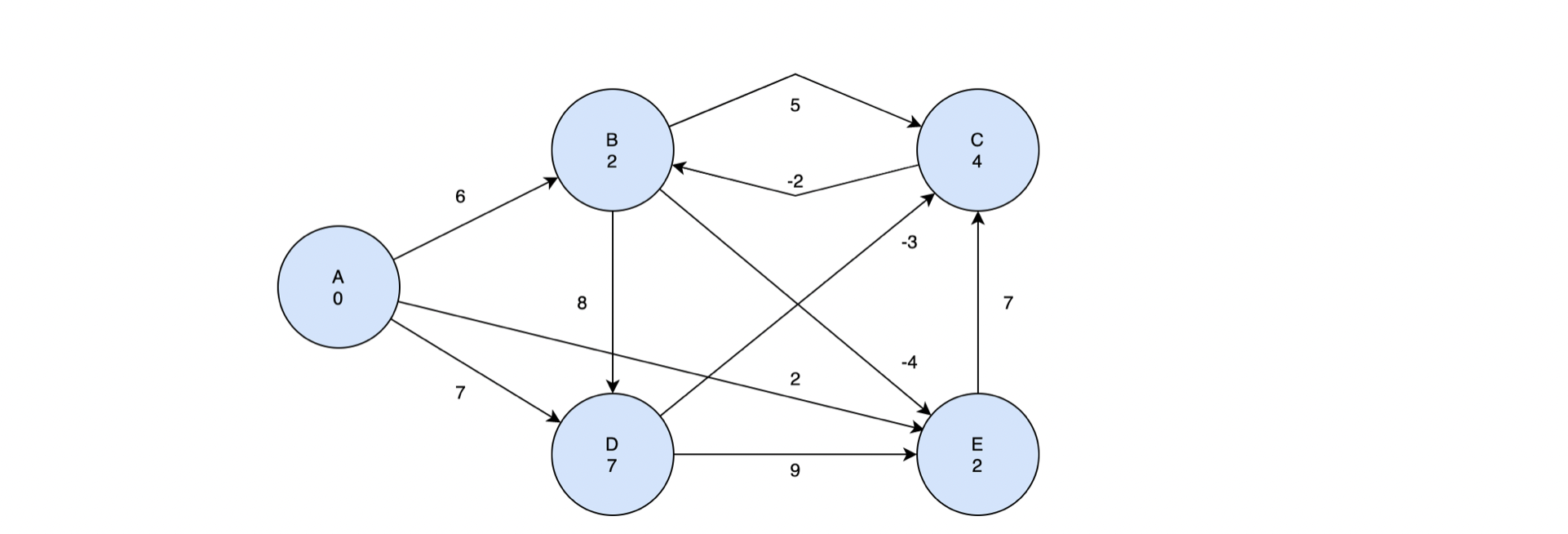
C에 대한 Relaxation을 진행해보자. 현재 정점 C까지의 최단경로를 거쳐서 B로 이동하게 되면, A에서 바로 B로 이동하는 거리보다 짧다. 따라서 B의 새로운 최단거리는 4 - 2 = 2 가 된다.
E정점에 대한 Relaxation을 진행하면 E를 거쳐 C로 가는 최단거리는 9이기 때문에 현재 C까지 가는 최단 경로보다 크다. 따라서 최단 경로를 업데이트 하지 않고 끝낸다. 이렇게 하면 한번의 relaxation 세트가 끝나게 된다. 이 작업을 시작 노드를 제외한 노드의 수 만큼 반복한다.
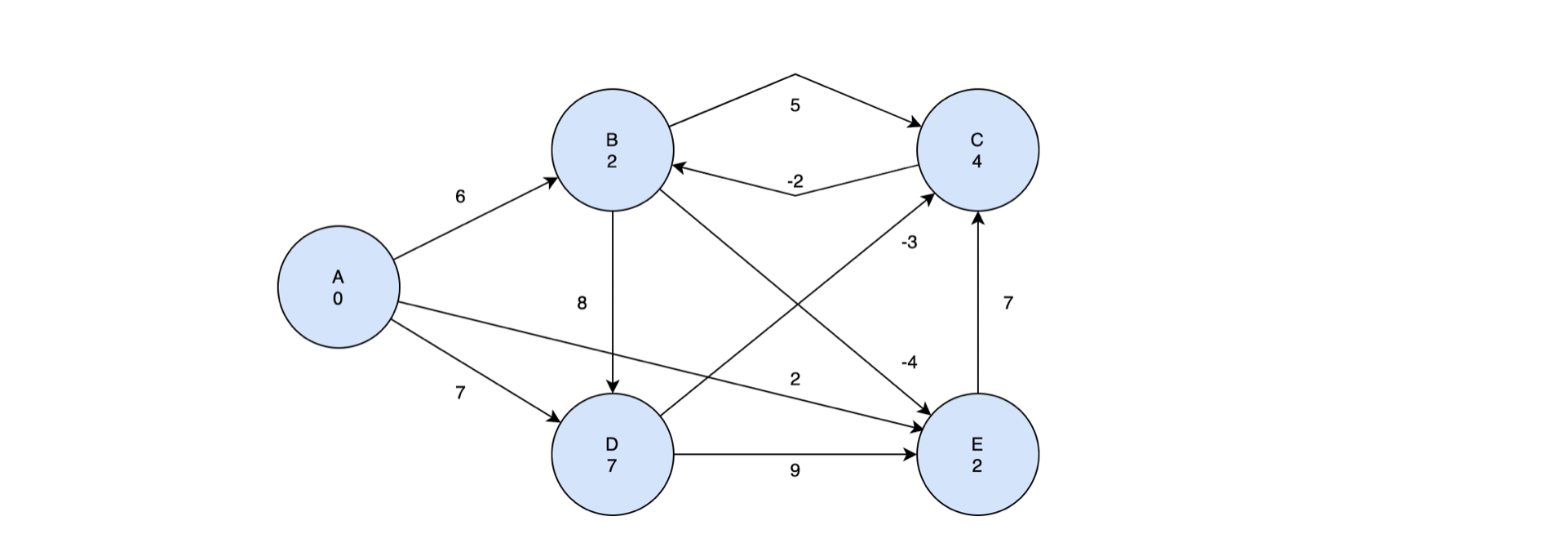
relaxation을 V-1 번 반복하게 되면 다른 간선들의 값은 변하지 않고 B에서 E로 가는 간선의 값이 업데이트 된다. 이 이후로 모든 rexlation 값은 변하지 않으므로 그래프 도식은 생략하기로 하겠다.
⭐️ Relaxation은 끝났지만, negative weight cycle이 있는지 확인하기 위해서 위 작업을 한번 더 거쳐야 한다. 현재 각 정점에 대한 최단거리가 기록되어 있는데 만약 이 거리가 새로운 최단거리로 갱신될 수 있다면, negative weight cycle이 존재한다는 의미일 것이다. 이때는 false 를 반환해서 지금까지 구한 최단거리가 의미가 없음을 알린다.
💻 C++ 구현
#include <iostream> #include <vector> #include <string> #define MAX_SIZE 500 #define INF 9999 using namespace std; int D[MAX_SIZE], Adj[MAX_SIZE][MAX_SIZE]; // Adj는 간선의 가중치를 저장할려고 하는 변수이기에 갱신 X, D는 최단거리를 저장해주는 변수이므로 갱신O int V,E ;// V는 정점, E는 간선 void Init_D(int sp); void Init_Adj(int sp); int main(){ int from,to,weight; // 그래프의 간선에 값을 넣기 위한 변수. int S; // 어디 정점부터 시작할지 입력. cout << "정점의 개수, 간선의 개수, 시작할 정점 위치를 입력하세요:\n"; cin >> V >> E >> S; Init_Adj(S); Init_D(S); /* 간선 정보 입력 */ for(int i=1;i<=E;i++){ cin >> from >> to >> weight; // 기본적인 간선 데이터 입력. 이 입력은 수정이 불가능. Adj[from][to] = weight; } /* 벨만-포드 알고리즘 */ for(int i = 1; i<V ; ++i){ for(from=1; from<=V ; ++from){ for(to = 1; to<=V ; ++to){ if( D[from] == INF ) continue; int dist = Adj[from][to] + D[from]; if ( D[to] > dist) D[to] = dist; } } } return 1; void Init_D(int S){ for(int i= 1;i<V;++i) D[i] = INF; D[S] = 0; // 초기 시작값은 0으로 초기화. } void Init_Adj(int S){ for(int i=1;i<V;++i) for(int j=1;j<V;++j) Adj[i][j] = INF; Adj[S][S] = 0; }
✏️ Leet code #743
📌 다익스트라를 이용한 풀이
class Dijkstra { public: int networkDelayTime(vector<vector<int>>& times, int n, int k) { vector<pair<int,int>> adj[n+1]; for(int i=0;i<times.size();i++) adj[times[i][0]].push_back({times[i][1],times[i][2]}); vector<int> dist(n+1,INT_MAX); priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> pq; pq.push({0,k}); dist[k]=0; while(!pq.empty()) { pair<int,int> t=pq.top(); pq.pop(); for(pair<int,int> it:adj[t.second]) { if(dist[it.first]>t.first+it.second) { dist[it.first]=t.first+it.second; pq.push({dist[it.first],it.first}); } } } int res=0; for(int i=1;i<=n;i++) { if(dist[i]==INT_MAX) return -1; res=max(res,dist[i]); } return res; } };
📌 벨만포드를 이용한 풀이
void Bellman_Ford() { Dist[1] = 0; for (int i = 1; i <= N - 1; i++) { for (int j = 0; j < Edge.size(); j++) { int From = Edge[j].first.first; int To = Edge[j].first.second; int Cost = Edge[j].second; if (Dist[From] == INF) continue; if (Dist[To] > Dist[From] + Cost) Dist[To] = Dist[From] + Cost; } } for (int i = 0; i < Edge.size(); i++) { int From = Edge[i].first.first; int To = Edge[i].first.second; int Cost = Edge[i].second; if (Dist[From] == INF) continue; if (Dist[To] > Dist[From] + Cost) { cout << "음수 간선 순환이 존재하는 그래프입니다." << endl; return; } } cout << "음수 간선 순환이 존재하지 않는, 정상적인 그래프 입니다." << endl; }
✏️ 백준 1916번
📌 다익스트라를 이용한 풀이
#include <bits/stdc++.h> using namespace std; #define INF 987654321 using pii= pair<int, int>; vector<pii> vec[1001]; vector<int> dist(1001, INF); void dijkstra(int dept){ dist[dept] =0; priority_queue<pii> pq; pq.push({dist[dept], dept}); // 시작 weight, vertex while(!pq.empty()){ int cur = pq.top().second; int distance = pq.top().first * -1; //현재까지 dept에서 cur 정점까지 가는 dist pq.pop(); if(dist[cur]<distance) continue; //이미 distance가 최소로 변경됨 for(int i=0; i<vec[cur].size(); i++){ int nxt=vec[cur][i].first; //cur 정점과 연결된 정점들 int nxtdist = vec[cur][i].second + distance; //현재까지 dept에서 cur정점까지의 최소 거리와 //cur을 지나 nxt까지의 거리를 더한것 cur정점에서 nxt까지의 distance // e.g) 1 -> 4(cur) -> 5(nxt) if(nxtdist<dist[nxt]){//만약 cur을 지나가는 것이 더 가깝다면 dist[nxt]= nxtdist; pq.push({nxtdist*-1, nxt});//새롭게 갱신된 weight와 vertex } } } } int main(){ int N, M; cin>>N>>M;//도시의 개수, 버스의 개수 while(M--){ int s, e, w; cin>>s>>e>>w; vec[s].push_back({e, w}); } int dept, dest; cin>>dept>>dest; dijkstra(dept); cout<<dist[dest]; return 0; }
📌 벨만포드를 이용한 풀이
#include <iostream> #include <vector> #define INF 987654321 using namespace std; /* 벨만포트 알고리즘 마지막 V번에서도 완화가 되면 음수 사이클이 존재함을 알려준다. */ int V,M; vector<pair<int, int> > v[1001]; int upper[1001]; int bellmanFord(int src) { //시작점 제외 모든 정점까지의 최단거리 INF로 초기화 fill_n(upper, 1001, INF); upper[src] = 0; bool updated; for(int i = 0; i < V; i++) { updated = false; for(int j = 1; j <= V; j++) for(int k = 0; k < v[j].size(); k++) { int there = v[j][k].first; int cost = v[j][k].second; if(upper[there] > upper[j] + cost) { // 완화 성공 upper[there] = upper[j] + cost; updated = true; } } if(!updated) break; //모든 간선에 대해 완화가 실패할경우 break; } if(updated) return 1; //음수 사이클이 존재 return 0; } int main(void) { //ios_base::sync_with_stdio(false); cin.tie(NULL); cin >> V >> M; for(int i = 0; i < M; i++) { int a,b,c; cin >> a >> b >> c; v[a].push_back(make_pair(b, c)); } int start, arrive; cin >> start >> arrive; if(!bellmanFord(start)) cout<<upper[arrive]; return 0; }