소수란 1보다 큰 자연수 중 3, 5, 7, 11처럼 1과 자기자신으로만 나누어지는 수를 말합니다.
코딩테스트에도 종종 등장하는 주제로 소수를 판별하는 방법은 어떤것들이 있는지 알아보겠습니다.
선형 탐색 (2 ~ N-1까지 반복문)
가장 단순한 방법으로 반복문을 사용해서 2부터 N-1까지 반복하며 나머지가 0으로 나오는 경우가 있는지를 확인하는 방법입니다.
function isPrime(num) {
// 2 미만의 수는 소수가 아니므로 false로 처리
if(num < 2) return false;
// 2 ~ N-1까지 반복하며 해당 수와 num을 나눴을 때
// 나머지가 0인 경우가 한번이라도 있다면 소수가 아니므로 false를 반환
for(let i = 2; i < num; i++) {
if(num % i === 0) return false;
}
return true;
}
console.log(isPrime(3)); // true
console.log(isPrime(4)); // false
console.log(isPrime(5)); // true
console.log(isPrime(10)); // false
console.log(isPrime(11)); // true단순하고 구현이 쉬운만큼 O(n)의 시간 복잡도를 가지고 있습니다.
제곱근 이용
이 방법은 약수의 특징을 이용한 방법입니다.
특정 수의 약수들의 중간을 기준으로 앞, 뒤의 수들은 몫과 나머지가 서로 반대되는 특징을 가지고 있습니다.
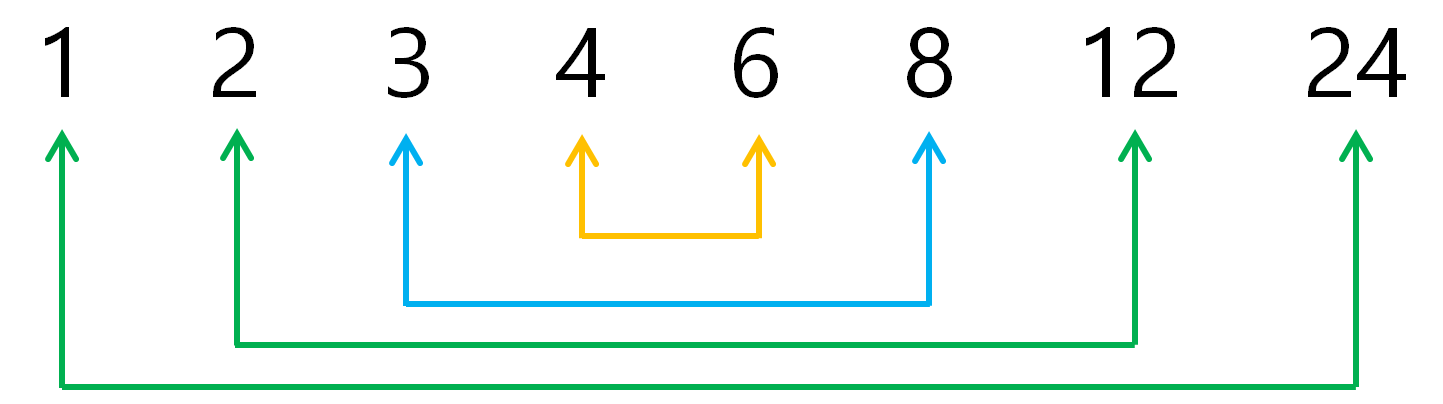
예를 들어, 24의 약수는 1, 2, 3, 4, 6, 8, 12, 24 이며 이들은 위 이미지처럼 중간을 기준으로 서로 대칭을 이루고 있습니다.
따라서, 굳이 대칭되는 수들을 반복해서 나눠 볼 이유가 없으므로 중간값과 가까운 수인 제곱근을 구한 뒤 제곱근까지만 반복문을 수행하여 불필요한 반복을 줄인 방법입니다.
function isPrime(num) {
// 2 미만의 수는 소수가 아니므로 false로 처리
if(num < 2) return false;
// 제곱근이 정수인 경우를 위해 `<=`로 표기 (Ex. 25)
for(let i = 2; i <= Math.sqrt(num); i++) {
if(num % i === 0) return false;
}
return true;
}
console.log(isPrime(2)); // true
console.log(isPrime(3)); // true
console.log(isPrime(4)); // false
console.log(isPrime(5)); // true
console.log(isPrime(10)); // false
console.log(isPrime(11)); // true
console.log(isPrime(25)); // false이 방법은 제곱근만큼만 반복하므로 O(sqrt(n))의 시간 복잡도를 가집니다.
다만, 지금까지의 방법들은 하나의 숫자가 소수인지를 판별해야할 때만을 위한 방법입니다.
만약, 여러개의 수가 소수인지 판별해야 한다면 각 수마다 위와 같은 반복문들을 수행해야하기 때문에 인풋의 크기가 증가하면 시간 복잡도 또한 비례하여 증가한다는 단점이 있습니다.
에라토스테네스의 체
2~N까지의 범위에 있는 수 중 소수가 아닌 수들을 체로 거르듯이 걸러낸다고해서 붙여진 이름입니다.
일정수까지 소수가 아닌 수들을 판별 후 제거하여 소수인 숫자만 남기는 방법입니다.
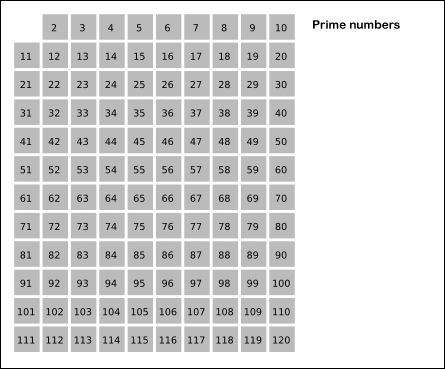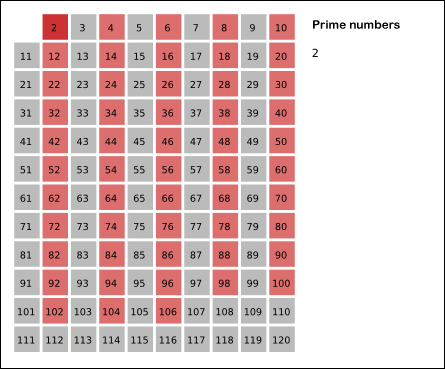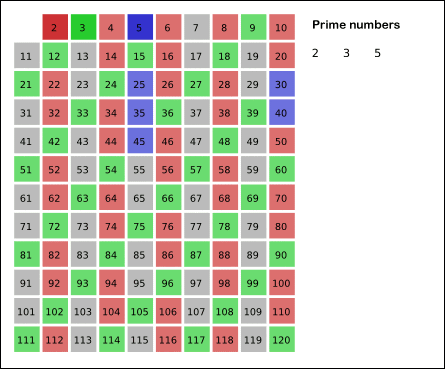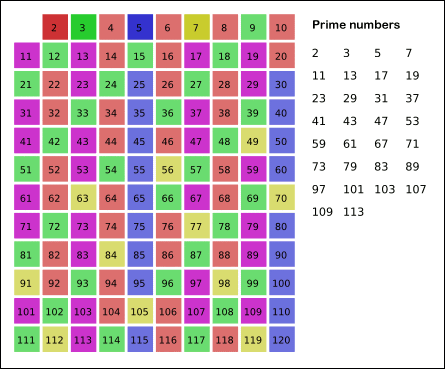
출처: 위키피디아
위 그림처럼 2부터 순환하며 소수인 수를 찾고 소수의 배수는 소수가 아니므로 걸러줍니다.
위에서 배웠던 제곱근을 이용한 방법을 사용해 n의 제곱근까지 작업을 해주면 소수인 수들만 남게 됩니다.
function getPrimeNums(num) {
// 소수를 판별할 수 있는 배열 생성 (소수 = true)
const primeNums = new Array(num).fill(true);
// 0과 1은 소수가 아니므로 false처리
primeNums[0] = false, primeNums[1] = false;
// 제곱근을 이용한 방법으로 소수판별
for(let i = 2; i <= Math.sqrt(num); i++) {
if(primeNums[i]) {
// 소수의 배수들은 소수가 아니므로 false처리
for(let j = i*2; j < num; j+=i) {
primeNums[j] = false;
}
}
}
return primeNums;
}
function isPrime(nums) {
const primeNums = getPrimeNums(Math.max(...nums));
return nums.filter(n => primeNums[n]);
}
console.log(isPrime([2, 5, 100]));