오늘은 탐색을 위해 사용되는 알고리즘인 선형탐색과 이분탐색에 대해서 알아보고 이 알고리즘을 사용하는 리트코드의 문제들도 함께 풀어보겠습니다.

선형 탐색 (= 순차 탐색, Linear Search)

선형 탐색 알고리즘은 원하는 데이터를 찾기 위해 한 쪽 끝에서 다른 쪽 끝까지 모든 요소를 차례로 순환하며 탐색하는 알고리즘입니다.
순서대로 순환하기 때문에 순차 탐색(Sequential Search)이라고도 합니다.

구현 난이도가 가장 쉽지만 인풋의 크기가 커질수록 시간 복잡도도 비례하여 증가한다는 단점이 있습니다.
따라서, 선형 탐색의 시간복잡도는 O(n)입니다.

선형 탐색 문제

이 문제는 리트코드의 2089번 문제로 숫자가 들어있는 nums배열과 찾아야 할 숫자 target이 인자로 주어집니다.

nums를 정렬한 뒤 탐색하여 target과 같은 요소들의 인덱스를 배열로 반환해야 합니다.

const targetIndices = function(nums, target) {
    const result = [];
    // nums의 요소들을 오름차 순으로 정렬
    nums.sort((a, b) => a - b);
    
    // 모든 요소들을 순환하면서 요소와 target이 같을 때 result 배열로 push
    for(let i = 0; i < nums.length; i++) {
        if(nums[i] === target) {
            result.push(i);
        }
    }

    return result;
};

console.log(targetIndices([1,2,5,2,3], 2)); // [1, 2]

console.log(targetIndices([1,2,5,2,3], 3)); // [3]

console.log(targetIndices([1,2,5,2,3], 5)); // [4]

이분 탐색 (= 이진 탐색, Binary Search)

이분 탐색은 요소들이 오름차순 혹은 내림차순으로 정렬되어있을 때 범위를 반씩 좁혀가며 요소를 찾는 알고리즘입니다.

구현 난이도가 그렇게 높지 않고 선형 탐색 대비 좋은 성능을 가지고 있으며 인풋의 크기가 커질수록 성능 차이가 더 크게 벌어집니다.

다만, 요소들이 꼭 정렬되어 있어야 하고 요소들이 높고 낮음 혹은 크고 작음과 같이 비교할 수 있는 대상이어야만 적용할 수 있습니다.

실생활에서도 종종 사용되는 알고리즘으로 시간 복잡도는 O(log n)이며 만약 0~9까지 오름차순으로 이루어진 배열이 있고 여기서 3이라는 숫자를 이분 탐색을 적용해 찾는 과정은 아래 그림과 같습니다.

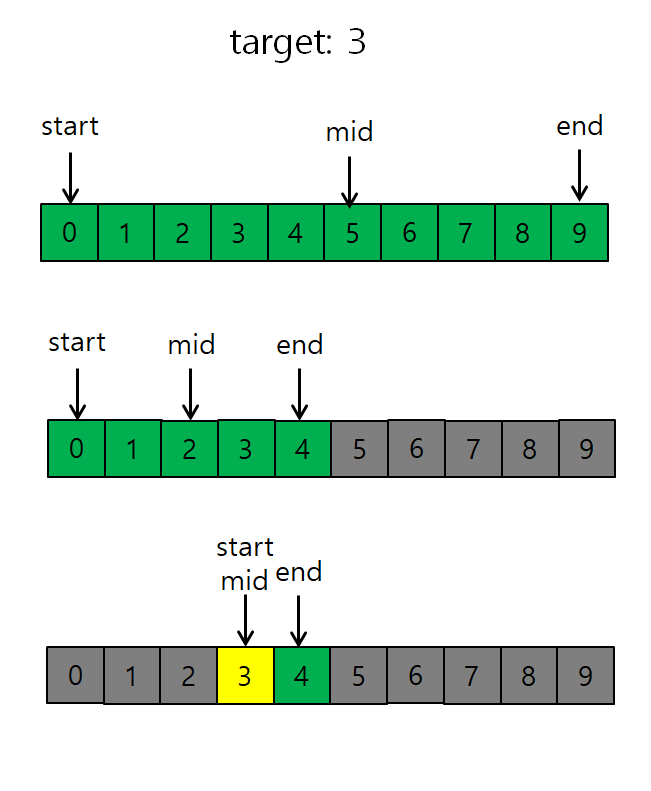
이분 탐색 문제

이 문제는 리트코드의 704번 문제로 숫자로 이루어져있으며 오름차순으로 정렬된 배열 nums와 찾아야 하는 숫자인 target이 인자로 주어지며 target과 같은 요소를 찾았다면 인덱스를 반환하고, 찾지 못했다면 -1을 반환하는 문제입니다.

const search = function(nums, target) {
    // 탐색 범위를 정하는 역할로 초기에는 첫번째와 마지막 인덱스를 지정합니다.
    let left = 0, right = nums.length - 1;
    
    // 만약 left가 right보다 커지게되면 해당 요소를 찾지 못한다는 뜻이므로 
    // 종료 후 -1을 반환합니다.
    while(left <= right) {
        // 현재 탐색 범위의 중간을 구합니다.
        const medium = Math.floor((left + right) / 2), midNum = nums[medium];

        if(midNum === target) return medium;

        // 중간값이 target보다 작다면 left를, 크다면 right를 변경해줍니다.
        if(midNum < target) {
            left = medium + 1;
        } else {
            right = medium - 1;
        }
    }

    return -1;
};