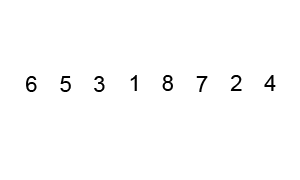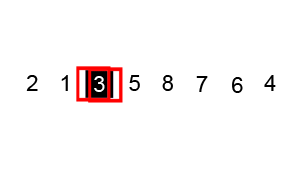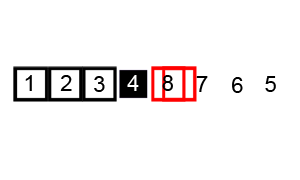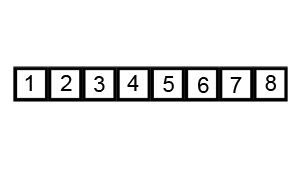
퀵 정렬은 많이 사용되는 정렬 알고리즘 중 하나로 분할 정복 알고리즘이자 불안정 정렬이라는 특징을 가지고 있습니다.
분할 정복 알고리즘의 특성상 정렬을 위해 요소들을 먼저 분할하게 되는데
퀵 정렬은 이 과정에서 기준이 되는 요소인 "피봇"을 정합니다.
오름차순 정렬이라고 가정했을 때 피봇을 제외한 나머지 요소들을 순환하며 피봇과 값을 비교하고 좌측에는 피봇보다 작은 값, 우측에는 피봇보다 큰 값을 정렬합니다.
이 때, 피봇을 제외한 요소들간의 정렬은 이루어지지 않습니다.
다만, 중요한 건 왼쪽에 있는 요소들은 피봇보다 작은 값, 오른쪽에 있는 요소들은 피봇보다 큰 값이며 피봇의 위치는 최종 위치가 됩니다.
따라서, 퀵 정렬은 한 번의 분할 과정이 끝나면 최소 한 개의 요소(피봇)는 정렬이 완료됩니다.
이러한 과정을 바탕으로 퀵 정렬은 최선 Ω(n log n), 평균 Θ(n log n), 최악 O(n^2)이라는 시간 복잡도를 가지게 됩니다.
구현
아래 로직은 오름차순 정렬을 기준으로 작성하였으며 가장 오른쪽에 위치한 요소가 피봇이 된다는 가정하에 작성하였습니다.
퀵 정렬에서는 두 개의 함수를 사용하는데 메인 함수인 quickSort 함수와
피봇을 잡고 피봇을 제외한 나머지 요소들을 순환하며 정렬하는 partition함수입니다.
quickSort 함수
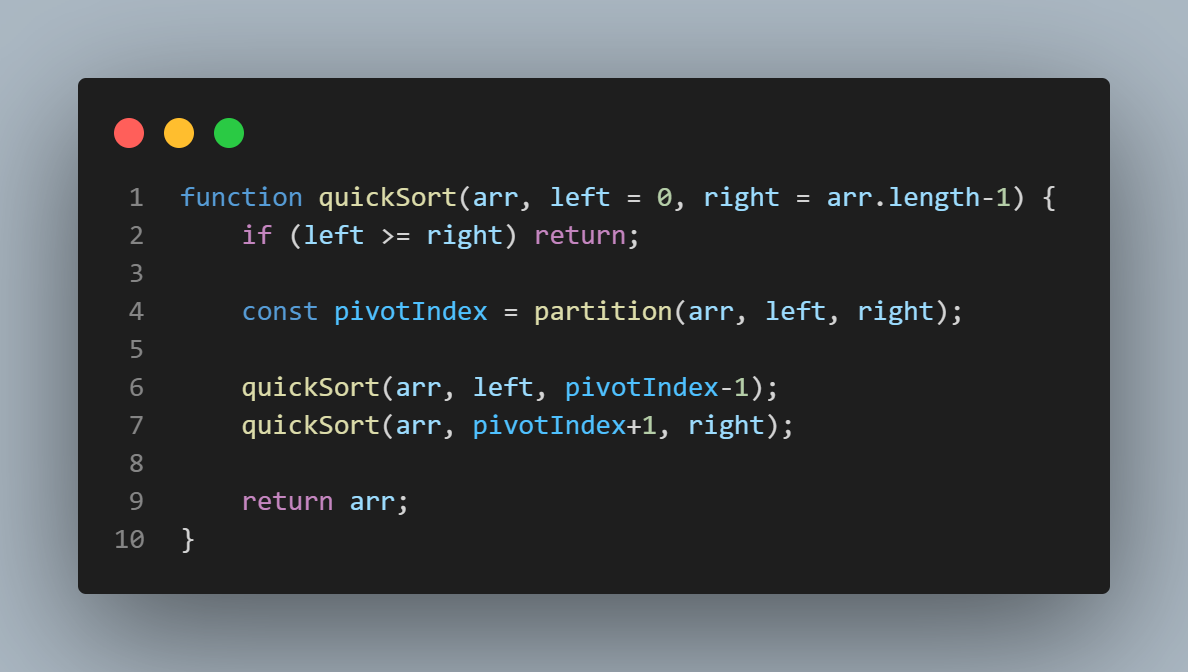
quickSort 함수는 재귀적으로 호출되는 함수로서 분할할 범위를 설정해야하기 때문에 left와 right라는 인자를 받습니다.
초기에는 전체 요소들을 순환해야하므로 left의 초기값은 0, right의 초기값은 arr.length-1로 기본 값을 설정해줍니다.
이후, partition 함수를 호출하는데 해당 함수로부터 피봇의 최종 인덱스를 반환받기 때문에 해당 피봇의 좌, 우측으로 영역을 나누어 재귀적으로 quickSort 함수를 호출하고 모든 과정이 완료되면 arr을 반환합니다.
partition 함수
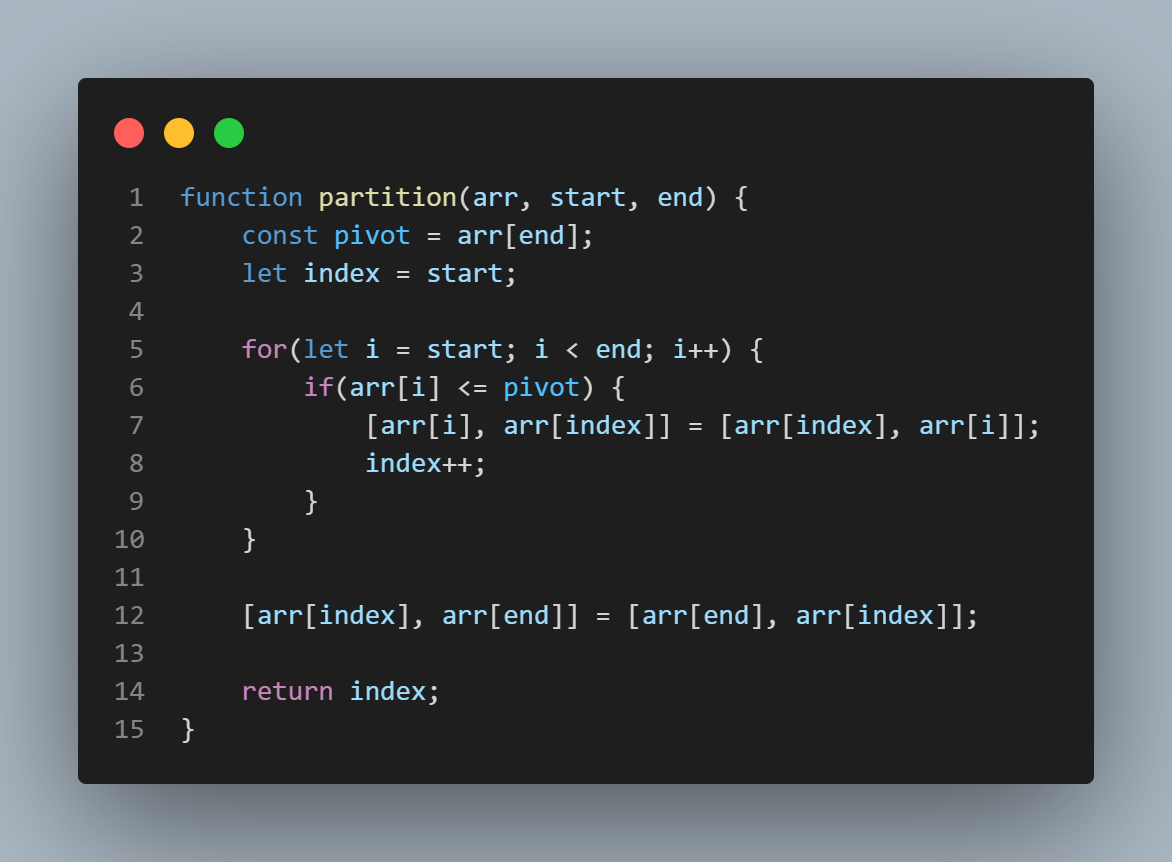
partition 함수에서는 가장 오른쪽 요소를 pivot으로 설정하고 pivot을 제외한 요소들을 순환하며 값을 비교합니다.
만약, 현재 정렬 대상 요소가 pivot보다 작거나 같다면 index위치의 요소와 스왑합니다.
이 과정을 통해 pivot보다 작은 요소는 왼쪽으로, 큰 요소는 오른쪽으로 정렬이 되며 for문이 종료될 때 index 변수의 최종 값은 pivot보다 큰 값 중에서 가장 왼쪽에 위치한 요소를 가르키게 됩니다.
index가 가르키고 있는 요소와 pivot을 스왑하게 되면 마침내 pivot은 자신의 최종 위치에 놓이게 됩니다.
이후, pivot의 최종 위치를 반환합니다.
전체 로직
퀵 정렬의 전체 로직입니다.
function partition(arr, start, end) {
const pivot = arr[end];
let index = start;
for(let i = start; i < end; i++) {
if(arr[i] <= pivot) {
[arr[i], arr[index]] = [arr[index], arr[i]];
index++;
}
}
[arr[index], arr[end]] = [arr[end], arr[index]];
return index;
}
function quickSort(arr, left = 0, right = arr.length-1) {
if (left >= right) return;
const pivotIndex = partition(arr, left, right);
quickSort(arr, left, pivotIndex-1);
quickSort(arr, pivotIndex+1, right);
return arr;
}
console.log(quickSort([4, 3, 10, 6, 8, 7, 9, 1, 2, 5]));아까 위에서 말한 시간 복잡도를 보면 다른 정렬 알고리즘과 비교했을 때 특별히 특출나진 않은 것 같은데 퀵 정렬은 왜 많이 사용될까요?
그 이유는 퀵 정렬의 시간 복잡도가 최악인 경우가 극히 드물기 때문입니다.
오름차순 정렬이라고 했을 때 퀵 정렬이 최악의 시간복잡도를 가지는 경우는 아래와 같은 두가지 경우입니다.
- 정렬해야하는 요소들이 정렬 목표와는 반대인 내림차순으로 정렬되어있는 경우
- 피봇에 저주가 걸려 매번 제일 작은 수를 고르는 경우
위와 같은 상황을 제외하면 일반적으로 n log n의 시간복잡도를 가지기 때문에 퀵 정렬의 시간복잡도를 얘기할 때 O(n log n) 이라고 하는 경우도 많습니다.
또한, O(n log n)의 일관된 시간복잡도를 가진 병합정렬과 비교했을 땐 공간복잡도에서 차이가 있습니다.
병합정렬의 경우, 정렬과정에서 인풋 크기만큼의 배열을 추가적으로 사용하기 때문에 O(n)의 공간복잡도를 가지지만 퀵 정렬은 O(log n)의 공간 복잡도를 가지며 이는 재귀함수 때문에 사용됩니다.
따라서, 위에서 말한 최악의 상황만 피할 수 있다면 퀵 정렬이 시간 + 공간복잡도면에서 병합정렬보다 더 좋은 성능을 가집니다.
위에서 말했듯이 최악의 시간복잡도가 발생하는 2번째 조건처럼 퀵 정렬에서 피봇이 어떤 요소를 잡느냐는 시간 복잡도에 많은 영향을 끼칩니다.
따라서, 위 로직처럼 고정적으로 잡는 경우도 있지만 운에 맡기는 랜덤 피봇 방식도 존재합니다.
그래서, 랜덤 피봇은 어떻게 구현하는지까지만 다뤄보겠습니다.
랜덤 피봇 퀵정렬
말 그대로 피봇만 랜덤으로 잡는것이기 때문에 위 로직과 크게 다르진 않으며 피봇 설정 부분만 다르게 작성해주면 됩니다.
랜덤 피봇 퀵정렬의 로직은 구현 방식이 조금씩 다를 수 있지만
이 글에서는 위에서 작성했던 로직을 활용해서 작성하였습니다.
function parition(arr, start, end) {
// const pivot = arr[end];
const randomIndex = Math.floor(Math.random() * (end - start) + start);
// 설정된 피봇을 맨 뒷자리 숫자와 스왑한다
[arr[end], arr[randomIndex]] = [arr[randomIndex], arr[end]];
// 스왑된 요소를 피봇으로 설정한다.
const pivot = arr[end];
let index = start;
for(let i = start; i < end; i++) {
if(arr[i] <= pivot) {
[arr[i], arr[index]] = [arr[index], arr[i]];
index++;
}
}
[arr[index], arr[end]] = [arr[end], arr[index]];
return index;
}partition 함수의 로직에서만 차이가 있는데 첫 번째로 start와 end를 활용해 랜덤값이 나올 범위를 잡아주고 이를 정수로 변환한 randomIndex 변수를 선언해줍니다.
이후, randomIndex의 요소와 가장 뒤에 위치한 요소를 우선적으로 스왑하여 피봇을 맨 뒤로 이동시켜주고 이를 pivot으로 설정해줍니다.
이후의 로직은 위에서 다뤘던 로직과 같습니다.
