오늘 다룰 알고리즘은 투포인터와 슬라이딩 윈도우 알고리즘입니다.

투포인터와 슬라이딩 윈도우 알고리즘은 배열, 리스트와 같은 선형 자료구조뿐만 아니라 문자열에서도 응용해서 사용할 수 있으며 특정 구간을 탐색할 때 유용합니다.

일반적으로 이 두 알고리즘을 적용할 수 있는 문제에서 알고리즘을 사용하지 않고 문제를 푸는 경우 O(n^2)까지의 시간 복잡도를 가지는 경우가 많습니다.

하지만, 이 알고리즘들을 적용 할 경우 O(n)의 시간복잡도로 해결이 가능하며 구현 난이도 또한 쉬운 편입니다.

투포인터 (Two Pointers)

투 포인터는 이름처럼 2개의 포인터를 사용해 배열의 특정 구간을 처리하거나 조사할 때 사용하며 하위 배열을 잡는 경우 일반적으로 두 개의 포인터는 각각 시작 지점과 끝 지점을 가르키게 됩니다.

그리고 문제해결 과정에서 원하는 결과를 얻을 때까지 두 개의 포인터를 조작합니다.

투포인터는 위에서 말했듯이 O(n)의 시간 복잡도로 문제를 해결할 수 있으며 데이터를 빠르게 처리할 때 유용하게 사용합니다.
또한, 정렬되어있지 않은 배열이 주어진다면 이진 탐색보다도 빠른 시간 복잡도를 가집니다.

투 포인터 예시 문제

정수들이 오름차순으로 정렬된 배열 nums와 정수 m을 매개변수로 받는 함수가 있다고 가정해보겠습니다.

주어진 배열에서 임의의 2개 요소를 더했을 때 m과 같다면 해당 요소들을 배열로 반환하고 해당하는 요소가 없다면 빈 배열을 반환해야하는 문제입니다.

이 문제를 풀 때 별도의 알고리즘을 사용하지 않고 2중 for문을 사용한다면 아래와 같이 코드를 작성할 수 있습니다.

function solution(nums, m) {
    for(let i = 0; i < nums.length-1; i++) {
        for(let j = i + 1; j < nums.length; j++) {
            if(nums[i] + nums[j] === m) {
                return [i, j];
            }
        }
    }

    return [];
}

console.log(solution([1, 3, 6, 7, 9], 10)); // [0, 4]
console.log(solution([1, 3, 5], 4)); // [0, 1]
console.log(solution([1, 2, 3, 4, 6, 7], 6)); // [1, 3]
console.log(solution([1, 9, 13, 20, 47], 10)); // [0, 1]

정답을 잘 반환하고 있지만 풀이 과정에서 2중 for문으로 인해 불필요한 중복 연산이 수행되었고 이에 따라 O(n^2)이라는 시간 복잡도를 가지게 되었습니다.

하지만, 이 문제에 투 포인터 알고리즘을 적용한다면 O(n)의 시간 복잡도로 해결이 가능합니다.

function solution(nums, m) {
    let start = 0, end = nums.length-1;
    
    while(start < end) {
        const sum = nums[start] + nums[end];

        if (sum === m) return [start, end];

        sum > m ? end-- : start++;
    }

    return [];
}

start와 end는 각각 시작 지점과 끝 지점을 가르키며 start가 end보다 작은 경우에만 반복합니다.

배열이 이미 오름차순으로 정렬되어 있기 때문에 현재의 합이 m보다 크다면 end의 인덱스를 1씩 줄이고,
반대로 작다면 start의 인덱스를 1씩 증가시켜 중복연산없이 문제를 풀어나갈 수 있습니다.

투 포인터는 위 문제처럼 주어진 배열에서 두 수의 합이 특정 값을 가지는 문제 말고도 배열의 연속된 요소를 더했을 때 임의의 값이 나오는 요소를 찾거나 토마토, 기러기처럼 회문 문자열(palindrome)을 판별하는 문제에서도 유용하게 사용할 수 있습니다.

슬라이딩 윈도우 (Sliding Window)

슬라이딩 윈도우 알고리즘은 배열에서 일정 크기의 구간을 이동하면서 문제를 해결하는 알고리즘입니다.

보통 배열의 부분합, 최솟값, 최댓값등을 구할 때 자주 사용되며 이름처럼 실생활에서 미닫이 창문을 열고 닫을 때 창문의 크기가 고정되어 있는 상태로 움직이는것을 연상하면 이해하기 쉽습니다.

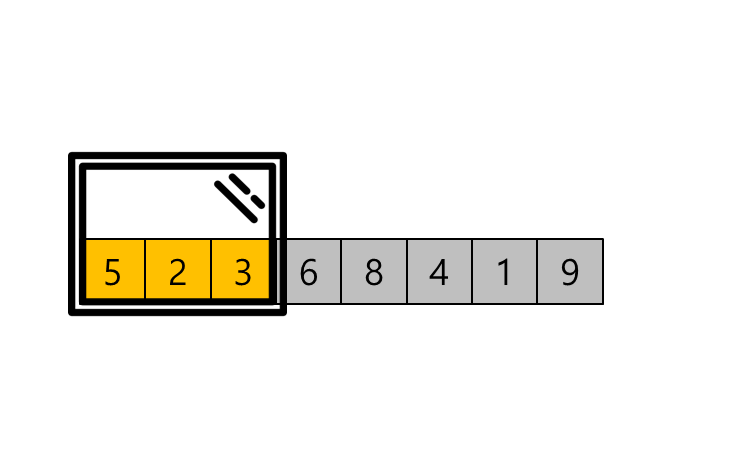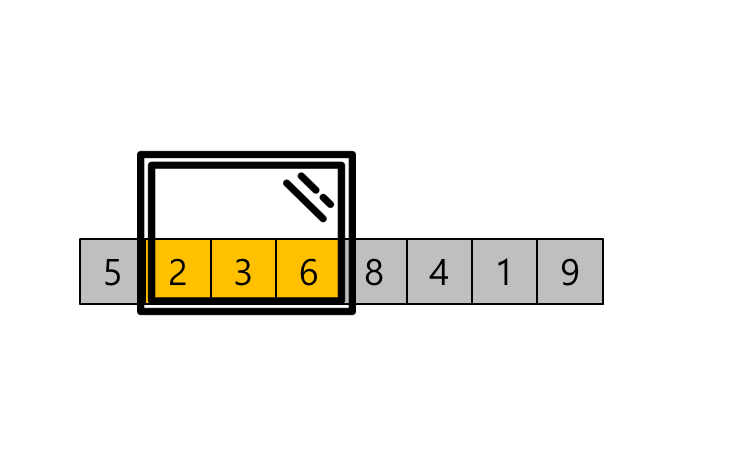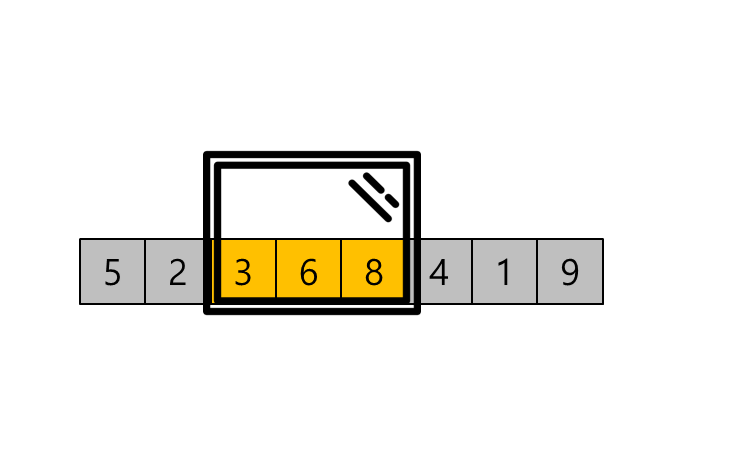
슬라이딩 윈도우 알고리즘은 투 포인터와는 다르게 하위 배열의 크기가 고정적이라는 특징이 있기 때문에 하위 배열에 대한 크기가 명시되어 있다면 슬라이딩 윈도우를, 명시되어 있지 않고 동적으로 변할 수 있다면 투 포인터 알고리즘을 적용해야 합니다.

슬라이딩 윈도우 예시 문제

이번에는 정수로 이루어진 배열 nums와 정수 k를 매개변수로 받는 함수가 있다고 해보겠습니다.

k는 요소의 개수를 뜻하며 k개의 연속된 요소를 더했을 때 나올 수 있는 최댓값을 반환해야 하는 문제입니다.

먼저, 일반적인 방법인 2중 for문을 사용한 풀이방법입니다.

function solution(nums, k) {
    let result = 0, temp = 0;

    for(let i = 0; i <= nums.length-k; i++) {
        temp = 0;

        for(let j = i; j < i + k; j++) {
            temp += nums[j];
        }

        result = Math.max(result, temp);
    }

    return Math.max(result, temp);
}

console.log(solution([100, 200, 300, 400], 2)); // 700

console.log(solution([1, 4, 2, 10, 23, 3, 1, 0, 20], 4)); // 39

정답은 잘 반환하지만 역시 문제는 시간복잡도입니다. 이 풀이의 시간복잡도는 O(n*k)입니다.

만약 이 문제에 슬라이딩 윈도우 알고리즘을 적용해보면 코드는 아래와 같습니다.

function solution(nums, k) {
    let result = 0, temp = 0;

    for(let i = 0; i < nums.length; i++) {
        if(i < k) {
            temp += nums[i];
            continue;
        }

        result = Math.max(result, temp);

        temp = temp - nums[i-k] + nums[i];
    }

    return Math.max(result, temp);
}

위 코드에서 result는 최댓값, temp는 현재 구간의 합을 의미합니다.

i가 k보다 작다면 아직 정해진 크기에 미치지 못하므로 temp에 현재 값을 더한 후 반복을 이어갑니다.

i가 k보다 같거나 크다면 크기를 충족하므로 temp와 result값 중 더 큰 값을 result에 반영하고 temp에는 해당 구간에 가장 앞에 위치한 값을 빼고 현재 값을 더해줍니다.

이렇게 되면 최종적으로 k만큼의 크기의 하위 배열 중 가장 큰 합이 result변수에 남아있게 됩니다.

또한, 슬라이딩 윈도우는 이 뿐만 아니라 두 문자열에서 공통된 부분 문자열을 찾는 문제, 흔히 LCS로 불리는 문제에도 적용할 수 있습니다.

정리

최종적으로 정리해보면 투 포인터와 슬라이딩 윈도우 알고리즘은 모두 배열과 같은 선형 자료구조에서 특정 구간을 탐색할 때 주로 사용하며 두 알고리즘은 모두 중복계산을 최소화하기 때문에 적용 가능한 조건이라면 O(n)의 시간복잡도로 문제를 해결할 수 있습니다.

투 포인터는 가변적으로 범위를 조정할 수 있고 슬라이딩 윈도우는 고정 범위를 가진 문제에만 적용할 수 있습니다.

기본적으로 슬라이딩 윈도우는 투 포인터보다 변수를 덜 사용하기 때문에 슬라이딩 윈도우가 적용 가능하다면 슬라이딩 윈도우를, 아니라면 투 포인터 알고리즘을 적용하면 되겠습니다.