프로그래머스/lv2/87946. 피로도

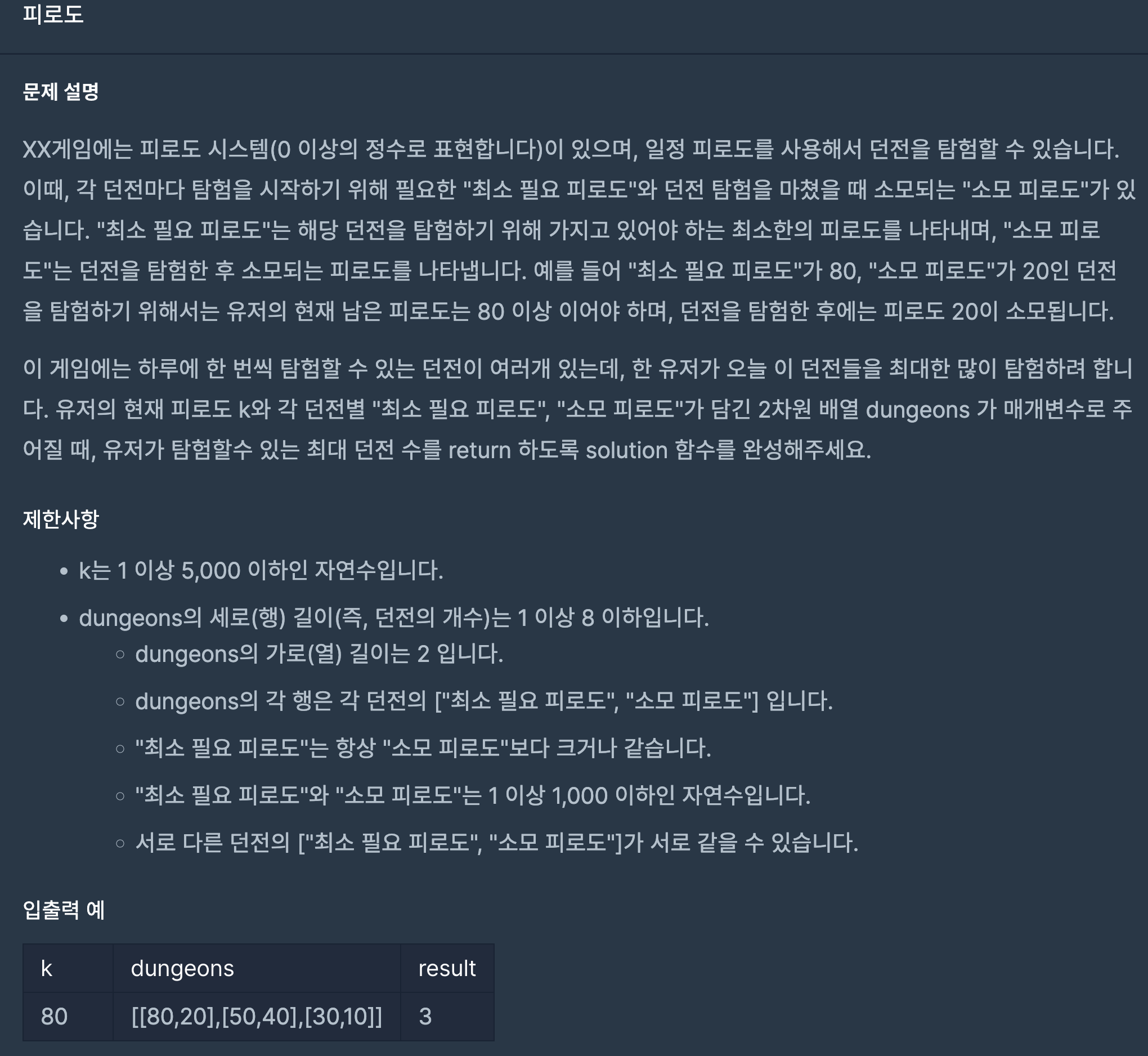
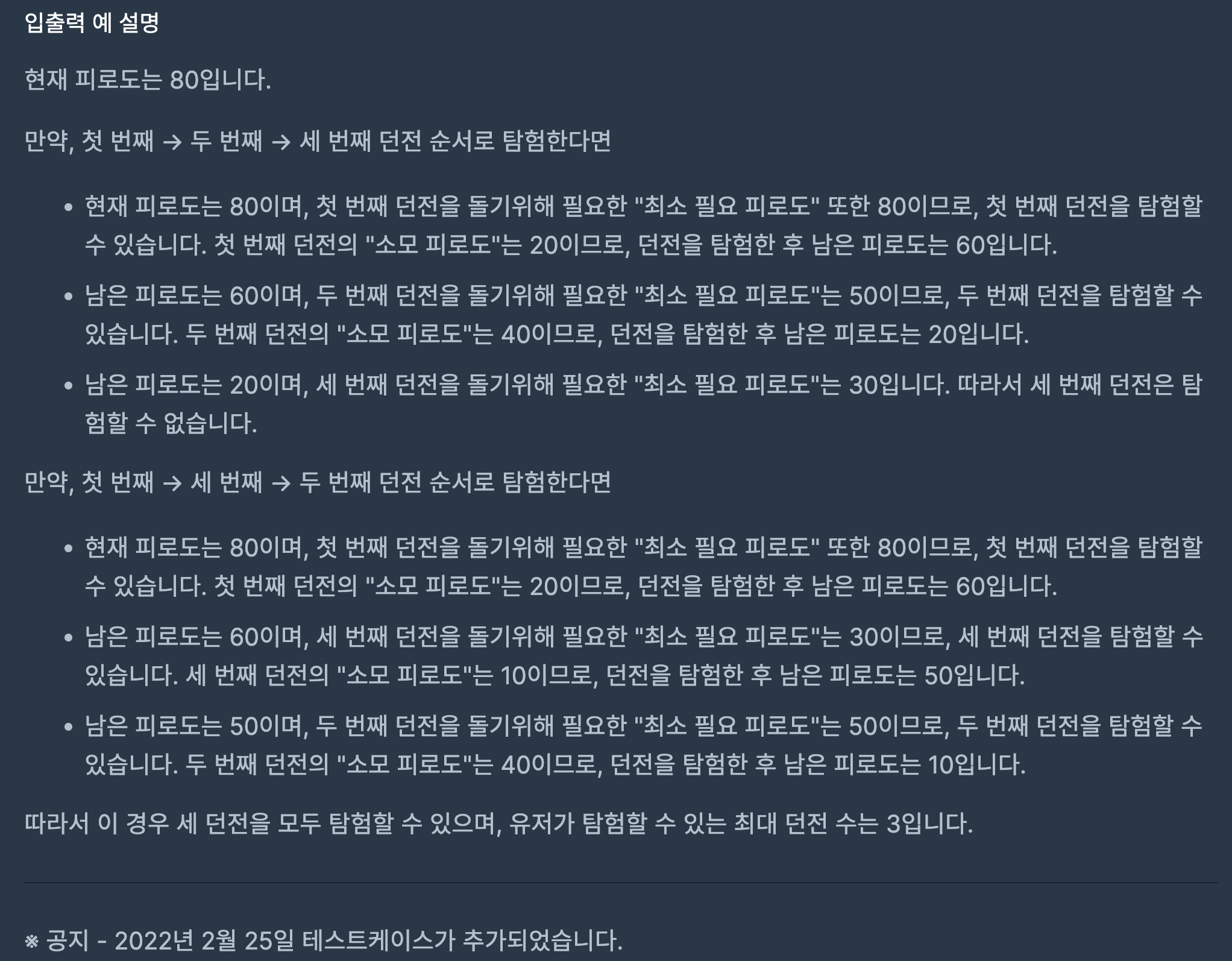
#include <string>
#include <vector>
#include <algorithm>
using namespace std;

int solution(int k, vector<vector<int>> d) {
    int answer = -1;

    vector<int> idx(d.size());

    for (int i = 0; i < d.size(); ++i) {
        idx[i] = i;
    }
    
    do {
        vector<vector<int>> p;
        for (int i = 0; i < d.size(); ++i) {
            p.push_back(d[idx[i]]);
        }
        int fatigue = k, cnt = 0;
        for (int i = 0; i < p.size(); i++) {
            if (fatigue >= p[i][0]) {
                cnt++;
                fatigue -= p[i][1];
            }
            else break;
        }
        answer = max(answer, cnt);
    } while (next_permutation(idx.begin(), idx.end()));

    return answer;
}

완전탐색 (Brute Force)문제였다. 던전 사이즈의 제약조건이 1부터 8밖에 되지 않기에 next_permutation() 을 사용해 모든 경우의 수를 체크하면 되는 문제였다.

index를 저장할 idx를 만들어주고, do while문을 돌면서 permutation을 반복할 vector p에 던전의 최소 피로도와 소요 피로도가 저장되어있는 d의 idx를 활용하여 한 개의 순열을 만들고,
피로도를 임시로 저장할 fatigue를 선언하고 매개변수로 들어온 k를 넣어준다.

그 뒤에 반복문을 돌면서 fatigue(현재 피로도)가 p[i][0] (입장할 수 있는 최소 피로도)를 만족한다면,
던전을 돌 수 있다는 의미이기에 cnt를 올려주고, p[i][1] (던전의 소요 피로도)를 빼준다.
하지만 조건을 만족하지 않는다면 더이상 피로도가 충분하지 않다는 것이니 반복문을 종료한다.
그 후 던전을 모두 완료한 후 cnt가 이전에 계산된 최댓값보다 크다면 answer의 값을 갱신해준다.