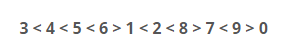👨💻 문제
✍️ 풀이
기본적으로 조합 문제이기에 백트래킹을 활용한다.
👶 1. 가장 만들기 쉬운 방법
- 만들 수 있는 모든 문자열을 만든다.
- 부등호에 알맞은 문자열인지 모두 검사한다.
- 처음과 마지막 문자열을 출력한다. (백트래킹을 통해 조합을 했으므로 정렬되어 있을 것이다.)
가장 확실하고 만들기도 편한 방법이다.
하지만 모든 문자열을 만든다는 것과,
모든 문자열을 모두 비교한다는 것이 너무 느리다.
🧒 2. 약간 더 빠른 방법
- 만들 수 있는 모든 문자열을 만든다.
- 처음부터 하나씩 부등호에 알맞는 문자열인지 검사하고 하나를 발견하면 검사를 멈춘다.
- 마지막부터 하나씩 부등호에 알맞는 문자열인지 검사하고 하나를 발견하면 검사를 멈춘다.
- 발견한 2개의 문자열을 출력한다.
1번 방식에 비해 부등호 확인 연산의 시간을 줄일 수 있다.
그래도 아직 모든 문자열을 만드는 건 너무 느리다.
🧑 3. 빠른 방법
- 문자열을 만듦과 동시에 부등호에 알맞은지 확인한다.
큰 숫자부터 조합하여 만들어지는 첫 번째 결과와
작은 숫자부터 조합하여 만들어지는 첫 번째 결과를 출력한다.
만들 수 있는 모든 문자열을 만들지 않는다는 것에서 큰 차이가 발생한다.
필자는 이 방법으로 구현했다.
👽️ 4. 더 빠른 방법 ?
< 부등호가 존재한다면 처음 숫자에 9가 올 수 없다.
> 부등호가 존재한다면 마지막 숫자에 0이 올 수 없다.
이런 방식으로 부등호의 수에 따라 큰 수가 앞에 올 수 있을지,
작은 수가 뒤에 올 수 있을지 예측할 수 있을 것이다.
좀 더 생각해보았다.
이웃한 연속된 부등호의 수로 가중치를 정할 수 있을 것 같다.
0 0 0 0 0 0 0 0 0 0
> < < < > > > < <
0 0 1 2 3 0 0 0 1 2 바로 왼쪽에 있는 연속된 <의 수
1 0 0 0 3 2 1 0 0 0 바로 오른쪽에 있는 연속된 >의 수
1 0 1 2 6 2 1 0 1 2 가질 수 있는 최소값 : 합
0 1 0 0 0 1 2 3 0 0 바로 왼쪽에 있는 연속된 >의 수
0 3 2 1 0 0 0 2 1 0 바로 오른쪽에 있는 연속된 <의 수
0 4 2 1 0 1 2 5 1 0 합
9 5 7 8 9 8 7 4 8 9 가질 수 있는 최대값 : 9 - 합이를 통해 각 자리마다 가질 수 있는 최소값과 최대값을 알 수 있다.
이를 범위를 바탕으로 백트래킹을 수행한다면 더 빠른 연산을 기대할 수 있을 것이다.
이 글을 쓰면서 생각난 가설이고, 실제로 적용해보진 않았다.
위 예제의 답
9567843012
1023765489📄 전체 소스코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.stream.Collectors;
public class Main {
private static int n;
private static char[] signs;
private static String largestNumber;
private static String smallestNumber;
private static int[] nums;
private static boolean[] usedNums;
public static void main(String[] args) throws IOException {
input();
nums = new int[n + 1];
usedNums = new boolean[10];
fillLargestNumber(0);
nums = new int[n + 1];
usedNums = new boolean[10];
fillSmallestNumber(0);
System.out.printf("%s\n%s\n", largestNumber, smallestNumber);
}
private static void input() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
signs = Arrays.stream(br.readLine().split(" ")).collect(Collectors.joining()).toCharArray();
}
private static void fillLargestNumber(int i) {
if (largestNumber != null) {
return;
}
for (int num = 9; num >= 0; num--) {
if (usedNums[num]) {
continue;
}
usedNums[num] = true;
nums[i] = num;
if ((i == 0) || (signs[i - 1] == '>' && nums[i - 1] > nums[i]) || (signs[i - 1] == '<' && nums[i - 1] < nums[i])) {
if (i == n) {
largestNumber = Arrays.stream(nums).mapToObj(String::valueOf).collect(Collectors.joining());
return;
}
fillLargestNumber(i + 1);
}
usedNums[num] = false;
}
}
private static void fillSmallestNumber(int i) {
if (smallestNumber != null) {
return;
}
for (int num = 0; num <= 9; num++) {
if (usedNums[num]) {
continue;
}
usedNums[num] = true;
nums[i] = num;
if ((i == 0) || (signs[i - 1] == '>' && nums[i - 1] > nums[i]) || (signs[i - 1] == '<' && nums[i - 1] < nums[i])) {
if (i == n) {
smallestNumber = Arrays.stream(nums).mapToObj(String::valueOf).collect(Collectors.joining());
return;
}
fillSmallestNumber(i + 1);
}
usedNums[num] = false;
}
}
}🔍️ 참고
fillLargestNumber() 메소드와 fillSmallestNumber() 메소드는
String 전역 변수와 반복문(0~9/9~0)만 다르다.
가장 큰 값을 찾으려는 메소드와 가장 작은 값을 찾으려는 메소드이기 때문에
기본적인 형태가 아예 똑같다.
이는 전역 변수들을 사용하지 않고 반환값을 지니게 하여 하나의 메소드로 리팩토링할 수 있다.
String largestNumber = makeNumber(new int[n + 1], new boolean[10], 0, true);
String smallestNumber = makeNumber(new int[n + 1], new boolean[10], 0, false);
...
private static void makeNumber(int[] nums, boolean[] usedNums, int i, boolean isLargest) {
...
for (int num = (isLargest ? 9 : 0); isLargest ? (num >= 0) : (num <= 9); num += (isLargest ? -1 : 1)) {
...
}