평균이나 중앙값은 데이터 분석을 잘 몰라도 이해하기 쉽지만, 분위수, 분산, 표준편차 등으 ㅣ통계량은 간단하게 설명하기 쉽지 않다. 게다가 통계량만 나열한 보고서라면 그 의미를 이해하기 더욱 어렵다.
전체 데이터를 한눈에 파악하려면 그래프가 가장 좋은 방법이다. 이번 절에서는 데이터를 그림으로 요약할 수 있는 대표적인 그래프인 산점도(scatter plot), 히스토그램(histogram), 상자수염그림(box and whisker plot)을 배운다!
산점도 그리기
산점도는 데이터를 화면에 뿌리듯 그리는 그래프이다. 조금 더 형식적으로 말하면 두 변수(variable) 또는 두 가지 특성(feature)값을 직교 좌표계에 점으로 나타내는 그래프이다.
+ 변수나 특성이 무엇인가요?
프로그래밍의 변수와는 다른 개념이다. 데이터 분석이나 머신러닝에서 변수는 한 레코드를 구성하는 개별 측정값을 의미한다. 특성이라고도 한다. 남산도서관 대출 데이터의 경우 '도서명', '저자' 등이 각각 하나의 변수이다. 즉 데이터프레임의 각 열이 하나의 특성이 되는 셈이다. 통계학에서는 특성 대신에 변수라는 용어를 자주 사용하지만, 이 책에서는 특성이란 용어를 주로 사용한다. 다만 특성 대신 특징, 속성 등으로 표현하는 책도 있다.
예를 들어 네 개의 데이터 포인트 (1, 1), (2, 2), (3, 3), (4, 4)을 화면에 점으로 표시하면 다음 그림과 같은 그래프가 그려진다. 이것이 산점도이다.
[255 그림삽임]
2차원 데이터를 나타낼 때 수평축을 x축, 수직축을 y축이라고 한다. 위 그림에서 데이터 포인트 (1, 1)에서 첫 번째 나오는 숫자가 x축의 값이고, 두 번째 숫자가 y축의 값이다.
그래프를 그리기 위해서는 별도의 패키지가 필요하다. 파이썬에서 그래프를 그리는 데 사용하는 대표적인 패키지는 맷플롯립(matplotlib)이다.
# ns_book7.csv 파일 다운로드
import gdown
gdown.download('https://bit.ly/3pK7iuu', 'ns_book7.csv', quiet=False)
# 판다스 데이터프레임으로 불러오기
import pandas as pd
ns_book7 = pd.read_csv('ns_book7.csv', low_memory=False)
ns_book7.head()
>>> 번호 도서명 저자 출판사 발행년도 ISBN 세트 ISBN 부가기호 권 주제분류번호 도서권수 대출건수 등록일자
0 1 인공지능과 흙 김동훈 지음 민음사 2021 9788937444319 NaN NaN NaN NaN 1 0 2021-03-19
1 2 가짜 행복 권하는 사회 김태형 지음 갈매나무 2021 9791190123969 NaN NaN NaN NaN 1 0 2021-03-19
2 3 나도 한 문장 잘 쓰면 바랄 게 없겠네 김선영 지음 블랙피쉬 2021 9788968332982 NaN NaN NaN NaN 1 0 2021-03-19
3 4 예루살렘 해변 이도 게펜 지음, 임재희 옮김 문학세계사 2021 9788970759906 NaN NaN NaN NaN 1 0 2021-03-19
4 5 김성곤의 중국한시기행 : 장강·황하 편 김성곤 지음 김영사 2021 9788934990833 NaN NaN NaN NaN 1 0 2021-03-19데이터가 준비되었다면 맷플롯립 패키지를 임포트하고 4개 포인트 (1, 1), (2, 2), (3, 3), (4, 4)로 이루어진 산점도를 그려보자. 맷플롯립에서 제공하는 그래프 함수는 matplotlib.pyplot 패키지 아래에 있다. 패키지 이름이 길어 plt로 줄여서 사용하는 것을 좋아한다.
import matplotlib.pyplot as pltscatter() 함수
산점도는 scatter() 함수로 그린다. 함수 첫 번쨰 매개변수에 4개 포인트의 x 축 좌표를 전달하고 두 번째 매개변수에 y축 좌표를 전달한다. 다음처럼 scatter() 함수를 호출한 다음에는 show() 함수를 호출하여 그래프를 출력한다.
plt.scatter([1,2,3,4], [1,2,3,4])
plt.show()
이번에는 남산도서관 대출 데이터를 사용해 산점도를 그려보자. 맷플롯립은 폋ㄴ리하게도 x축과 y축 값으로 데이터프레임의 열을 입력받을 수 있다. 남산도서관 대출 데이터 중에서 '번호' 열의 값을 x축에 넣고 '대출건수' 열의 값을 y축에 넣어보자.
plt.scatter(ns_book7['번호'], ns_book7['대출건수'])
plt.show()
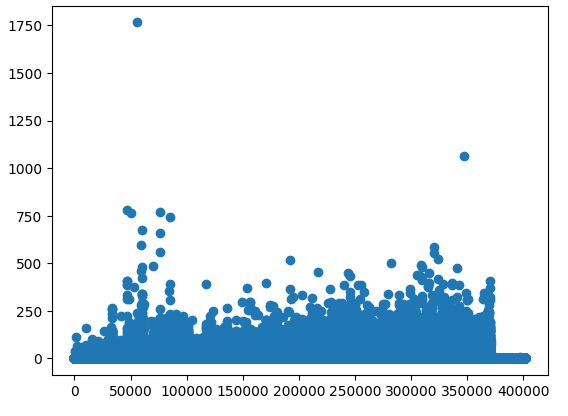출력된 그래프 보면 데이터가 많이 겹쳐져 있다. x축에 놓인 '번호' 열의 값을 따라 대출건수가 어떻게 변하는가?
사실 '번호' 열은 원본 대출 데이터에서 각 행에 붙여진 일렬번호이다. 이런 일렬번호는 데이터(도서)를 구분하기 위한 용도이므로 특별한 의미를 가지지 않는다. '번호' 열의 값이 낮거나 높다고 대출 건수가 달라지지 않을 가능성이 높다. 따라서 위에 출력된 산점도에서도 이런 경향을 잘 볼 수 있다. 대출건수(y축의 값)는 번호(x축의 값)를 따라 비교적 고르게 퍼져있다.
+ 맷플롯립은 다양한 그래프 설정을 지원한다. 예를 들어 x축과 y축에 이름을 지정할 수도 있다. 이 절에서는 분포를 표현하는 대표적인 그래프를 배우는 데 집중하고, 다양한 맷플롯립 옵션은 5장에서 자세히 다룬다.
그럼 '번호' 열 말고 '도서권수'와 '대출건수' 열의 산점도를 살펴보자. 이전과 마찬가지로 scatter() 함수의 첫 번째 매개변수에는 x축에 해당하는 '도서권수' 열을 지정하고, 두 번째 매개변수에는 y축에 해당하는 '대출건수' 열을 지정한다.
plt.scatter(ns_book7['도서권수'], ns_book7['대출건수'])
plt.show()
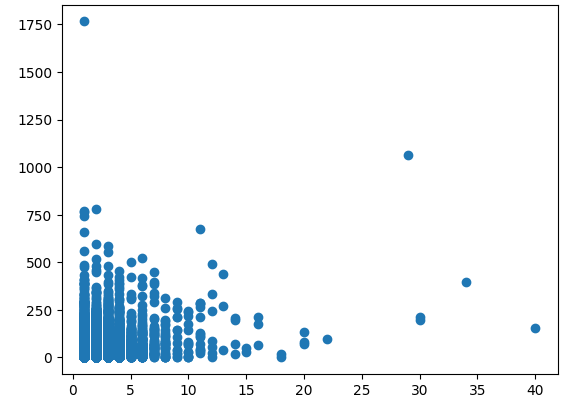도서권수가 많으면 대출건수도 많을 것이라 예상하기 쉽지만, 앞의 산점도를 보면 이런 경향을 파악하기 쉽지 않다. 특히 대부분의 도서가 1-2권이기 때문에 x축 0-10 범위인 왼쪽 아래 모서리 부분에 같은 값을 가진 데이터 포인트가 중첩되어 그려진다. 이럴 때는 산점도에 투명도를 주면 중첩된 데이터 포인트를 가늠하기 좋다.
투명도 조절하기
맷플롯립은 aplha 매개변수에 0-1 사이의 값으로 투명도를 지정할 수 있다. 투명도를 주더라도 데이터가 많이 중첩된 부분은 짙게 나타난다. 이 매개변수를 0.1로 지정하여 산점도를 다시 그려보자.
plt.scatter(ns_book7['도서권수'], ns_book7['대출건수'], alpha=0.1)
# 'alpha=0.1' : 투명도 지정. 0에 가까울수록 투명하고 1에 가까울수록 불투명하게 그려짐.
plt.show()
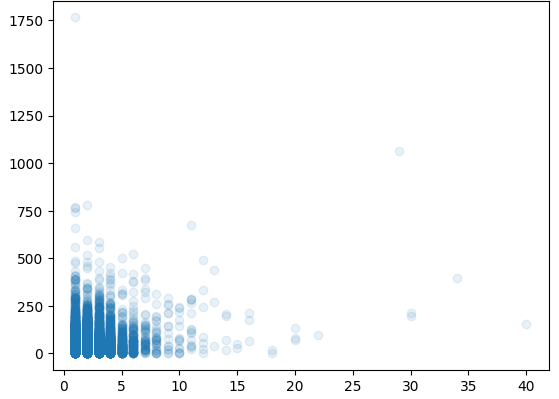예상대로 왼쪽 아래 모서리 근처에 중첩된 데이터 포인트가 많다. 투명도를 더 낮추더라도 왼쪽 아래 모서리 근처는 여전히 짙게 나타나는데, 이는 대부분의 도서권수가 적다는 것을 의미한다.
도서권수가 대부분 작은 값이기 때문에 도서권수와 대출건수 사이의 관계를 파악하기 어렵다. 여기서 도서권수와 대추건수 사이의 관계란 도서권수가 많으면 대출건수도 많다던가. 도서권수가 적을수록 대출건수가 많다는 식이다. 이러면 전자는 양의 상관관계, 후자는 음의 상관관계가 있다고 말한다.
이번에는 '도서권수' 열 대신에 '대출건수' 열을 '도서권수' 열로 나눈 값을 사용해보자. 도서권수 당 대출건수를 x축에 두고 대출건수를 y축에 놓는다. 눈썰미 있다면 두 값은 양의 상관관계를 가질 것이라고 예상 가능!! 대출건수가 높다면 도서권수 당 대출건수도 당연히 톺다.
'대출건수' 열을 '도서권수' 열로 나눈 값을 average_borrows 변수에 저장하고, 이 변수와 '대추건수' 열을 차례대로 scatter() 함수에 전달한다. 여기에서도 alpha 매개변수를 0.1로 지정한다.
average_borrows = ns_book7['대출건수']/ns_book7['도서권수']
plt.scatter(average_borrows, ns_book7['대출건수'], alpha=0.1)
plt.show()
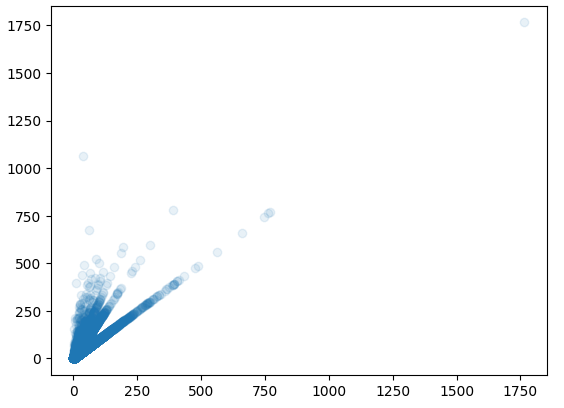
# 양의 상관관계출력된 그래프를 보면 x축(도서권수 당 대출건수)이 증가함에 따라 y축(대출건수)가 증가하는 것을 뚜렷하게 볼 수 있다. 두 특성 사이에는 '양의 상관관계가 있다'고 말할 수 있다.
산점도는 데이터를 2차원 좌표에 점으로 뿌려서 표현하기 때문에 데이터 분포를 한 눈에 볼 수 있는 유용한 도구이다. 하지만 2차원 또는 3차원 산점도만 가능하기 때문에 한 번에 표현할 수 있는 특성 개수에 한계가 있다.
히스토그램 그리기
히스토그램은 수치형 특성의 값을 일정한 구간으로 나누어 구간 안에 포함된 데이터 개수를 막대 그래프로 그린 것이다. 구간 안에 속한 데이터 개수를 도수(frequency)라고 부른다.
히스토그램의 예를 그림으로 나타내면 다음과 같다. 아래 그래프는 네 개의 구간으로 나누어진 히스토그램이다 구간마다 도수의 높이가 다르다. 첫 번째 구간(0-5)에는 10개의 데이터가 들어가 있기 때문에 도수가 10이다. 두 번째 구간(5-10)에는 20개의 데이터가 포함되어 있어 도수가 20이 되는 식이다.
hist() 함수
맷플롯립으로 히스토그램을 그릴 때는 hist() 함수를 사용한다. hist() 함수는 1차원 데이터를 입력받아 히스토그램을 그리며, 기본적으로 데이터를 10개의 구간으로 나눈다.
간단한 샘플 데이터로 히스토그램을 어떻게 그리는지 알아보자. 8개의 정수로 이루어진 간단한 데이터를 사용한다. bins 매개변수를 5로 지정하여 5개의 구간으로 그려보자.
plt.hist([0,3,5,6,7,7,9,13], bins=5)
# 'bins=5' : 데이터를 5개의 구간으로 나눈다.
plt.show()
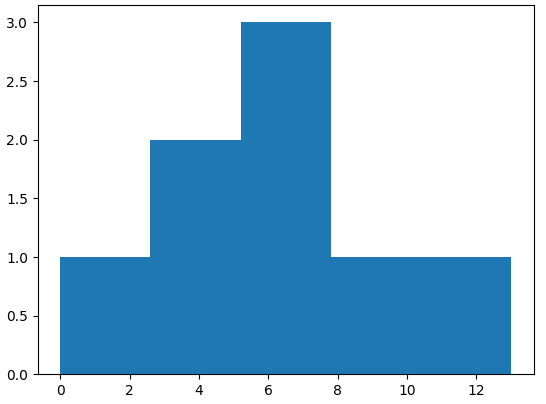어느 구간에 데이터가 많은지 한눈에 잘 보이지만, 구간이 어떻게 나누어졌는지 수치를 확인할 수 없다. 히스토그램의 구간을 정확하게 확인하기 위해 넘파이에서 제고하는 histogram_bin_edges() 함수를 사용하자.
import numpy as np
np.histogram_bin_edges([0,3,5,6,7,7,9,13], bins=5)
>>> array([ 0. , 2.6, 5.2, 7.8, 10.4, 13. ])첫 번째 구간은 0-2.6까지이다. 두 번째 구간은 2.6-5.2까지이다. 이때 경계값 2.6은 두 번째 구간에 포함된다.
이제 더 많은 데이터를 가상으로 만들어 히스토그램을 그려 보자! 넘파이의 randn() 함수는 표준정규분포를 따르는 랜덤한 실수를 생성할 수 있다. 이 함수에 원하는 샘플 개수를 전달하여 난수(random number)를 생성해보자.
np.random.seed(42)
random_samples = np.random.randn(1000)이 코드는 랜덤한 실수를 1,000개 생성한다. seed() 함수를 사용하면 유사난수(pseudorandom number)를 생성할 수 있다. 즉, 가짜 난수이다!
randn() 함수는 랜덤한 값을 생성하기에 실행할 때마다 다른 값이 추출된다. 실제로 randn() 함수만 실행하면 이 책과 결과가 다를 것이다! 문제는 안되지만, 책이나 튜토리얼과 실습 결과 동일하게 만들기 위해 seed() 함수를 사용한다. 따라서 seed() 함수에 책과 동일한 값을 사용하는 한 언제나 동일한 난수를 추출할 수 있다.
# 1000개의 실수로 이루어진 random_samples 배열이 표준정규분포를 따르고 있는지 확인위해 평균과 표준편차를 계산해보자.
print(np.mean(random_samples), np.std(random_samples))
>>> 0.01933205582232549 0.9787262077473543실행 결과 보면 random_samples의 평균이 약 0.02, 표준편차가 약 0.98이므로 표준정규분포를 따르고 있다고 볼 수 있다.
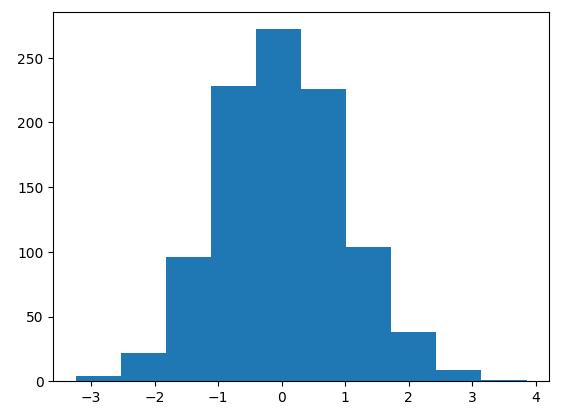
히스토그램을 그려서 종 모양의 분포가 나오는지 확인해 보면, 다음과 같이 평균 0을 중심으로 볼록한 종 모양의 분포가 그려진 것을 알 수 있다.
plt.hist(random_samples)
plt.show()
그럼 남산도서관 대출 데이터에서 수치 데이터의 분포를 확인하기 위해 히스토그램을 그려보자!
# '대출건수' 열의 히스토그램 그리기.
plt.hist(ns_book7['대출건수'])
plt.show()
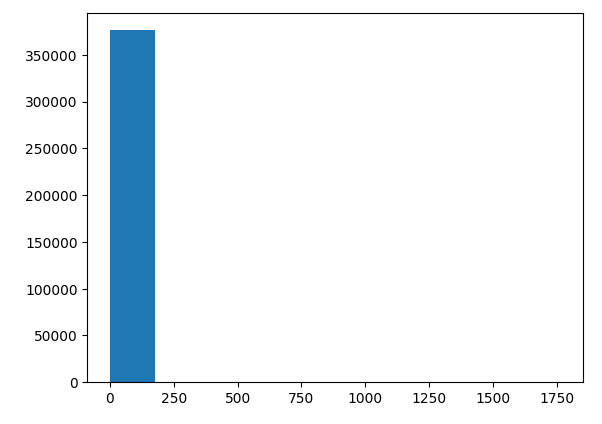산점도에서 보았듯이 대부분 도서의 대출건수는 작다. 따라서 앞의 그림과 같이 첫 번째 구간의 도수가 너무 커서 다른 구간에는 도수 값이 표시되지 않는 현상이 발생한다.
구간 조정하기
한 구간의 도수가 너무 커서 다른 구간에는 도수가 표시되지 않는 현상이 발생하면 y축을 로그 스케일로 바꾸어 해결할 수 있다. 로그 스케일(log scale) 로 바꾼다는 것은 다음 그림처럼 y축에 로그 함수를 적용한다는 의미이다. 그러면 큰 값일수록 도수 크기가 많이 줄어들어 작은 값과의 차이가 줄어든다.
[265 그림삽입]
맷플롯립에서 y축을 로그 스케일로 바꾸려면 다음처럼 yscale() 함수에 'log'를 지정하면 된다.
plt.hist(ns_book7['대출건수'])
plt.yscale('log')
plt.show()
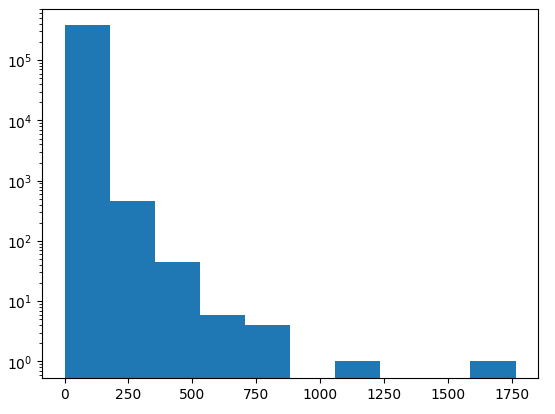맷플롯립은 기본적으로 밑이 10인 로그 함수를 사용한다. 그래서 y축의 눈금 스케일이 10^0에서 10^5까지 나타나 있다.
예를 들어 첫 번째 구간의 도수는 약 370,000 정도이다. 로그 스케일로 변환된 그래프에서는 10^5 다음에 작은 눈금이 2 x 10^5, 즉 200,000을 의미한다. 그 다음 작은 눈금이 300,000이다. 첫 번째 구간의 도수는 300,000은 넘지만 400,000에 채 못 미치는 것을 알 수 있다.
이번에는 x축의 구간을 더 세세하게 나누어보자! hist() 함수는 기본 10개의 구간을 사용한다. bins 매개변수에서 이를 100으로 바꾸면 데이터 분포를 조금 더 세밀하게 관찰할 수 있다.
plt.hist(ns_book7['대출건수'], bins=100)
# 'bins=100' : 구간을 100개로 나눈다.
plt.yscale('log')
plt.show()
확실히 대출건수 0이 가장 ㅁ낳고 대출건수가 증가함에 따라 도수가 줄어든다. 이런 그래프는 정규분포와는 거리가 멀다. 이번에는 조금 다른 데이터의 히스토그램을 그려보자.
도서명 길이는 정규분포에 가까울까? 다음처럼 '도서명' 열에 apply() 메서드를 사용하여 파이썬의 len() 함수를 적용하면 title_len 변수는 각 도서명의 길이가 저장된 판다스 시리즈 객체가 된다. 이를 100개의 구간을 가진 히스토그램으로 그려보자.
title_len = ns_book7['도서명'].apply(len)
# 'apply(len)' : 데이터프레임에 len() 함수를 반복 적용한다.
plt.hist(title_len, bins=100)
plt.show()
대출건수만큼은 아니지만 왼쪽에 편중된 그래프이다. x축에 데이터가 골고루 그려지도록 바꿀 수 없을까?
앞에서 y축에 로그 스케일을 적용했던 것처럼 x축에도 로그 스케일 적용할 수 있다. 이렇게 하면 x축을 따라 작은 값과 큰 값의 차이가 줄어들 것이다. y축에 로그 스케일을 적용하는 yscale() 함수와 비슷하게 xscale() 함수를 사용하면 된다.
plt.hist(title_len, bins=100)
plt.xscale('log')
plt.show()
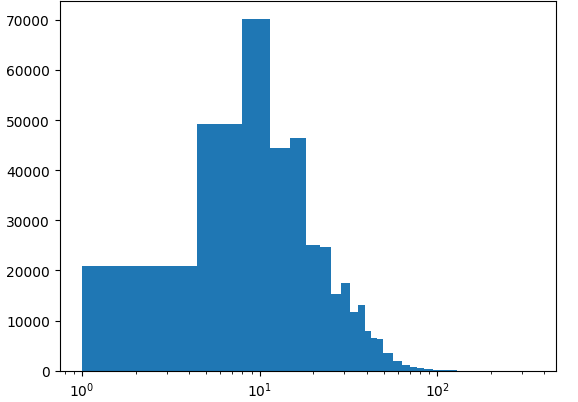히스토그램은 이처럼 하나의 특성에 대한 분포를 확인하기 좋다. 전체 데이터가 어떻게 ㅓ져있는지 한눈에 파악하기 쉽다. 하지만 여러 개의 특성을 비교하려면 각기 따로 그린 히스토그램을 비교해야 한다. '대출건수'와 '도서권수' 열을 그린 히스토그램에서 볼 수 있듯이 x축과 y축의 범위가 다르다. 이 두 그래프를 잘 비교하려면 각 축의 범위를 맞추어 그려야한다. 조금 더 편리하게 여러 특성의 분포를 비교할 수 있는 방법이 있을까?
상자 수염 그림 그리기
상자 수염 그림은 최솟값, 세 개의 사분위수, 최댓값 이렇게 다섯 개의 숫자를 사용해 데이터를 요약하는 그래프를 그린다. 상자 수염 그림을 그리는 방법은 다음과 같다.
① 먼저 사분위수를 계산한다. 25%와 75% 지점을 밑면과 윗면으로 하는 직사각형을 그린다.
② 중간값, 즉 50%에 해당하는 지점에 수평선을 긋는다.
③ 사각형의 밑면과 윗면에서 사격형의 높이의 1.5배만큼 떨어진 거리 안에서 가장 멀리 있는 샘플까지 수직선을 긋는다.
④ 이 수직선 밖에서 최솟값과 최댓값까지 데이터를 점으로 표시한다. 이 영역의 데이터를 이상치(outer)라고 부른다.
제1사분위수(25% 백분위수)와 제3사분위수(75% 백분위수)사이의 거리를 IQR(interquartile range)이라고 한다.
[269 그림삽입]
상자 수염 그림은 여러 개의 특성을 시각적으로 비교하기 좋다. 특히 데이터가 어떤 방향으로 더 많이 늘어져 있는지 한눈에 파악 가능하다.
+ 이상치는 데이터에서 꼭 제거해야 하나요?
데이터 과학이나 머신러닝에서 관측 범위에서 아주 많이 벗어난 값 혹은 데이터에 내재한 패턴을 크게 벗어난 값을 이상치라고 한다. 이상치는 머신러닝 모델에 큰 영향을 미칠 수도 있기 때문에 모델을 훈련하기 전에 삭제할 수 있다. 하지만 상자 수염 그림에 나오는 이상치는 단순히 IQR의 1.5배 거리 밖의 데이터를 의미하며, 데이터 분석에서의 이상치는 데이터 양이 많을수록 영향이 줄기 때문에 반드시 제거해야 하는 것은 아니다.
boxplot() 함수
남산도서관 대출 데이터에서 '대출건수'와 '도서권수' 열의 상자 수염 그림을 그려보자! 맷플롯립에서 상자 수염 그림은 boxplot() 함수로 그린다.
temp = ns_book7[['대출건수','도서권수']]
plt.boxplot(temp)
plt.show()
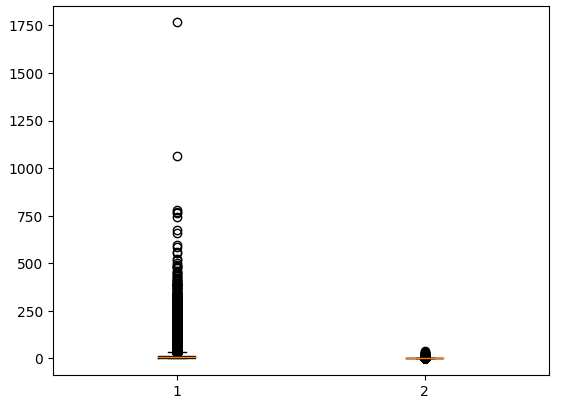1번 상자(대출건수)와 2번 상자(도서권수) 데이터는 사분위수가 매우 작아서 직사각형 상자가 거의 보이지 않는다. 중간값은 붉은 수평선으로 표시된다.
plt.boxplot(ns_book7[['대출건수','도서권수']])
plt.yscale('log')
plt.show()
y축을 로그 스케일로 바꾸어도 2번 상자(도서권수)는 여전히 보이지 않지만, 1번 상자(대출건수)는 상자 모양을 뚜렷하게 확인할 수 있다. 사실 '도서권수' 열의 사분위수는 모두 1이기 때문에 상자가 보이지 않는 것이 맞다!
상자 수염 그림 수평으로 그리기
수평으로 그려야할 경우, boxplot() 함수의 vert 매개변수를 기본값 True에서 False로 바꾸면 된다. x-y축이 바뀌므로 로그 스케일도 x축에 지정해야 한다 히스토그램과 마찬가지로 xscale() 함수를 사용한다.
plt.boxplot(ns_book7[['대출건수','도서권수']], vert=False)
plt.xscale('log')
plt.show()
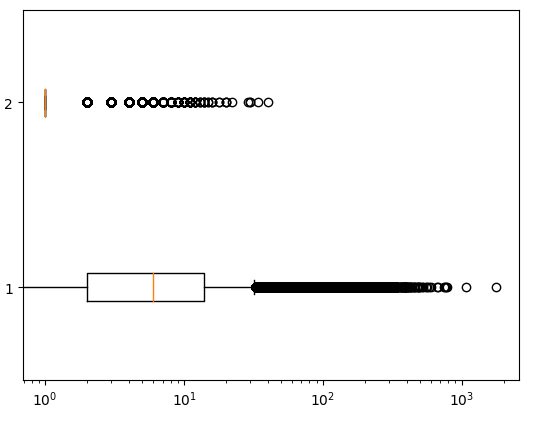수염 길이 조정하기
기본적으로 수염의 길이는 IQR의 1.5배이다. 하지만 더 길게 혹은 더 짧게 나타낼 수 있다.
boxplot() 함수의 whis 매개변수에서 이를 조정할 수 있다.
plt.boxplot(ns_book7[['대출건수','도서권수']], whis=10)
# 'whis=10' : 수염 길이를 조정한다.
plt.yscale('log')
plt.show()
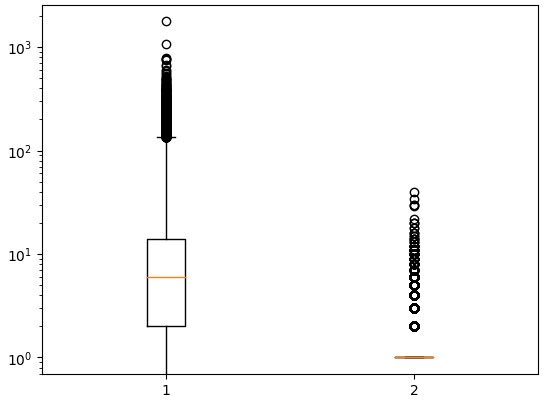확실히 수염이 길어졌다! 2번 상자(도서권수)의 IQR은 0이기 때문에 여전히 수염이 전혀 그려지지 않는다.
whis 매개변수는 백분율로도 지정할 수 있다. 예를 들어 (10, 90)으로 지정하면 10%, 90% 백분위수에 해당하는 데이터까지 수염을 그린다.
# (0, 100)으로 지정
plt.boxplot(ns_book7[['대출건수','도서권수']], whis=(0,100))
plt.yscale('log')
plt.show()
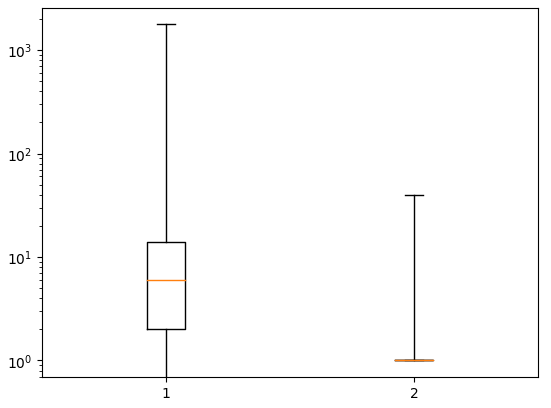수염의 길이를 백분위수로 지정하니 2번 상자(도서권수)에도 수염이 그려진다!
통계량을 시각적으로 표현하기
데이터를 2차원 평면에 점을 표시하는 산점도, 데이터를 일정 구간으로 나누어 구간에 속한 데이터 개수를 막대 그래프로 나타내는 히스토그램 그리고 마지막으로 사분위수와 최솟값, 최댓값을 사용해 그리는 상자 수염 그림을 그려봤다.
좀더 알아보기 판다스의 그래프 함수
산점도 그리기
판다스 데이터프레임 객체의 plot 속성은 여러 가지 그래프를 그릴 수 있는 메서드를 제공한다. 이 중 scatter() 메서드로 산점도를 그릴 수 있다. 맷플롯립과 달리 데이터프레임으로 그래프를 그릴 때는 다음처럼 x축과 y축에 해당하는 열 이름만 지정하면된다.
ns_book7.plot.scatter('도서권수', '대출건수', alpha=0.1)
# '도서권수' : x축, '대출건수' : y축, 'alpha=0.1' : 투명도 지정 가능
plt.show()
scatter() 메서드는 x축과 y축 이름을 자동으로 열 이름으로 표시하는데, 열 이름이 한글일 때는 실행 결과처럼 제대로 출력 안된다. 이를 해결하려면 한글 폰트를 사용하도록 지정해야 하는데, 코래은 한글 폰트를 가지고 있지 않기에 따로 폰트를 설치해야 한다.
히스토그램 그리기
히스토그램은 hist() 메서드로 그릴 수 있다. 도서명 길이에 대한 분포를 그려보면 다음과 같다. 맷플롯립으로 그릴 때는 도서명 길이에 대한 객체를 따로 생성했었는데, 판다스는 다음처럼 데이터프레임에 apply() 메서드를 적용한 다음 이어서 바로 plot.hist() 메서드를 호출할 수 있어 간편하다.
ns_book7['도서명'].apply(len).plot.hist(bins=100)
plt.show()
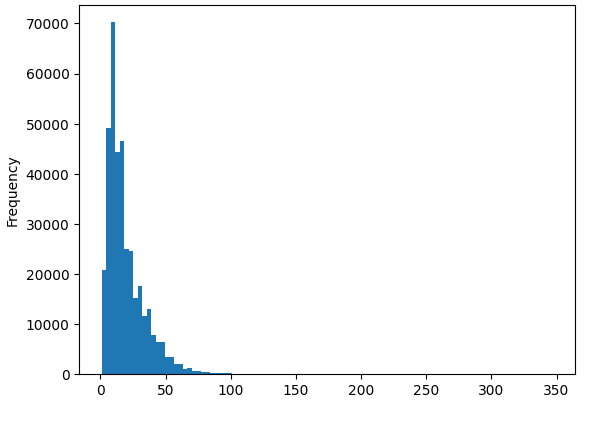상자 수염 그림 그리기
상자 수염 그림은 boxplot() 메서드로 그린다.
ns_book7[['대출건수','도서권수']].boxplot()
plt.yscale('log')
plt.show()
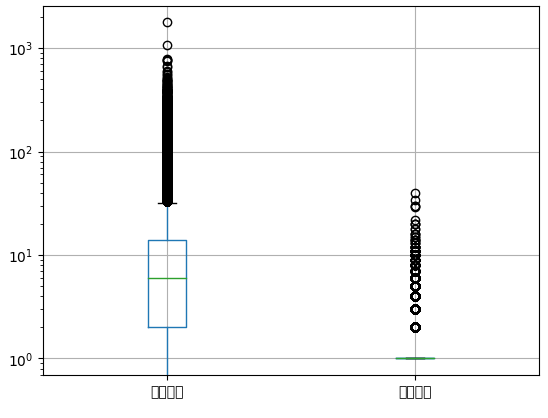x축에 자동으로 열 이름이 나오지만, 한글 폰트 문제 때문에 제대로 출력이 되지 않는다.
판다스로 그린 그래프 결과가 모두 맷플롯립으로 그렸을 때와 유사하다! 이는 판다스에서 그래프 출력을 위해 기본적으로 맷플롯립 패키지를 사용하기 때문이다. 지원하는 매개변수도 매우 비슷하다. 주로 판다스 데이터프레임을 사용해 데이터를 다룬다면 판다스에서 제공하는 그래프 기능을 사요하는 것이 더 편리할 때도 많다.
정리
- 맷플롯립은 파이썬의 대표적인 그래프 패키지이다. 산점도, 히스토그램, 상자 수염 그림을 비롯하여 막대 그래프, 선 그래프 등 많은 종류의 그래프를 지원한다. 또한 그래프의 구성 요소를 다양하게 제어할 수 있는 많은 옵션을 제공한다.
- 산점도는 데이터를 2차원 평면 또는 3차원 공간에 점으로 표시하는 그래프이다. 차워늬 제약으로 일반적으로 두 개 또는 세 개의 특성을 표현할 수 있지만, 점의 색까을 달리하옇 ㅏㄴ 개의 특성을 더 표현할 수 있다.
- 히스토그램은 데이터를 일정 구간으로 나누어 국나에 속한 데이터 개수(도수)를 막대로 표현하는 그래프이다. 데이터가 어떤 부분에 집중되어 분포되어 있는지 잘 볼 수 있다.
- 그래프가 한쪽에 편중되어 그려진다면 x, y축을 로그 스케일로 바꾸어 그릴 수 있다. 수치를 로그로 간결하게 표시할 수 있어 넓은 범위의 데이터를 표시하기 좋다.
- 상자 수염 그림은 사분위수, 최솟값, 최댓값을 사용해 여러 특성의 분포를 비교할 수 있는 그래프이다. 제 1사분위수와 제 3사분위수를 사용해 상자를 그리고, 상자의 IQR 거리의 1.5배 범위 안에서 가장 멀리 떨어진 데이터까지 수직선(수염)을 그려서 분포를 표현한다.
핵심 함수와 메서드
- Matplotlib.puplot.scatter() : 2차원 평면에 산점도를 그린다.
- Matplotlib.puplot.hist() : 히스토그램을 그린다.
- Matplotlib.puplot.boxplot() : 상자 수염 그림을 그린다.
- Matplotlib.puplot.xscale() : x축의 스케일을 지정한다.
- Matplotlib.puplot.yscale() : y축의 스케일을 지정한다.
- numpy.random.seed() : 원하는 임의의 정수를 입력하면 난수 발생을 동일하게 재현할 수 있다.
- numpy.random.seed() : 표준정규분포를 따르는 난수를 생성한다.