혼자 공부하는 머신러닝 + 딥러닝 02-2 데이터 전처리

넘파이로 데이터 준비하기

넘파이의 column_stack() 함수 : 전달받은 리스트를 일렬로 세운 다음 차례대로 나란히 연결. 연결할 리스트는 튜플(tuple)로 전달.

튜플(tuple) : 리스트처럼 원소에 순서 있지만, 한 번 만들어진 튜플은 수정 불가.

import numpy as np

np.column_stack(([1, 2, 3], [4, 5, 6]
>>> array([[1, 4],
		   [2, 5],
           [3, 6]])

이처럼 fish_lenght와 fish_weight 합치기!

fish_data = np.column_stack((fish_length, fish_weight))

#리스트 연결 잘 되었는지 처음 5개 데이터 확인
print(fish_data[:5])
>>>[[ 25.4 242. ]
    [ 26.3 290. ]
    [ 26.5 340. ]
    [ 29.  363. ]
    [ 29.  430. ]]

np.concatenate () 함수 : 첫 번째 차원을 따라 배열을 연결하는 함수.

fish_target = np.concatenate((np.ones(35), np.zeros(14)))

print(fish_target)
>>> [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0.]

사이킷런으로 훈련 세트와 테스트 세트 나누기

넘파이 배열의 인덱스를 직접 섞어서 훈련 세트와 테스트 세트 나눔 → 번거로움!!
train_test_split() 함수 : 전달되는 리스트나 배열을 비율에 맞게 훈련 세트와 테스트 세트로 나누어줌!!! 나누기 전에 섞어도 줌!!

from sklearn.model_selection import train_test_split

train_input, test_input, train_target, test_target = train_test_split(
    fish_data, fish_target, random_state=42)

train_test_split() 함수에는 자체적으로 핸덤 시드 지정할 수 있는 random_state 매개변수 있음!!

fish_data와 fish_target 2개의 배열 전달했으므로 2개씩 나뉘어 총 4개의 배열 반환. 차례대로 처음 2개는 입력 데이터(train_input, train_target)에, 나머지 2개는 2개의 타깃 데이터(train_target, test_target)에 들어감.

print(train_input.shape, test_input.shape)
>>> (36, 2) (13, 2)

print(train_target.shape, test_target.shape)
>>> (36,) (13,)

훈련 데이터와 테스트 데이터를 각각 36개, 13개로 나누었음. 입력 데이터는 2개의 열이 있는 2차원 배열이고 타깃 데이터는 1차원 배열.

print(test_target)
>>> [1. 0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1.]

13개의 테스트 세트 중, 10개가 도미(1), 3개가 빙어(0). 잘 섞인 것 같지만 빙어의 비율이 조금 모자라다. 원래 도미와 빙어의 개수 35개, 14개의 비율은 2.5:1 이지만, 위 테스트 데이터 의 비율은 3.3:1이다. 이것이 바로 데이터 편향!!

하지만 train_test_splite() 함수에는 이를 해결할 수 있는 방법 있음! stratify 매개변수에 타깃 데이터를 전달하면 클래스 비율에 맞게 데이터 나눠준다. 훈련 데이터가 작거나 특정 클래스의 샘플 개수가 적을 때 특히 유용!!

train_input, test_input, train_target, test_target = train_test_split(
    fish_data, fish_target, stratify=fish_target, random_state=42)
    
print(test_target)
>>> [0. 0. 1. 0. 1. 0. 1. 1. 1. 1. 1. 1. 1.]

이제 비율이 2.25:1이 되면서 비슷하게 되었다.

수상한 도미 한 마리

앞서 준비한 데이터로 k-최근접 이웃 훈련.

from sklearn.neighbors import KNeighborsClassifier

kn = KNeighborsClassifier()
kn.fit(train_input, train_target)
kn.score(test_input, test_target)
>>> 1.0

print(kn.predict([[25, 150]]))
>>> [0.]


import matplotlib.pyplot as plt

plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()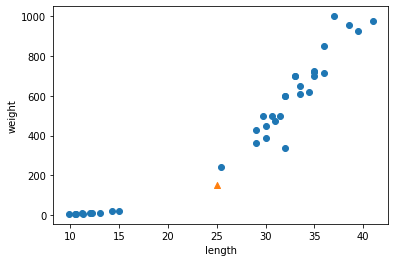

샘플은 분명 오른쪽 위로 뻗어 있는 도미 데이터에 더 가까운데 모델은 왼쪽 아래 낮게 깔린 빙어 데이터에 가깝다고 나왔다.

KNeighborsClassifier 클래스는 주어진 샘플에서 가장 가까운 이웃을 찾아주는 kneighbors() 메서드 제공한다. 이 메서드는 이웃까지의 거리와 이웃샘플의 인덱스를 반환한다.

distances, indexes = kn.kneighbors([[25, 150]])

plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()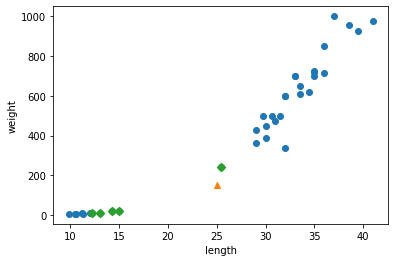

가장 가까운 이웃에 도미가 하나 밖에 없음. 나머지 4개의 샘플은 모두 빙어다.

# 직접 데이터 확인

print(train_input[indexes])
>>> [[[ 25.4 242. ]
  [ 15.   19.9]
  [ 14.3  19.7]
  [ 13.   12.2]
  [ 12.2  12.2]]]
--> 가장 가까운 생선 4개는 빙어(0) 같다.

# 타깃으로 명확히 확인
print(train_target[indexes])
>>> [[1. 0. 0. 0. 0.]]

길이 25cm, 무게 150g인 생선에 가장 가까운 이웃엔 빙어가 압도적으로 많음. 따라서 이 샘플의 클래스로는 빙어 예측하기에 무리가 있다.

해결을 위해 kneighbors() 메서드에서 distances 배열을 출력해보자. 이는 이웃 샘플까지의 거리가 담겨 있다.

print(distances)
>>> [[ 92.00086956 130.48375378 130.73859415 138.32150953 138.39320793]]

기준을 맞춰라

위 산점도에서 보듯이, 삼각형 샘플로부터 왼쪽 마름모까지의 길이는 130, 오른쪽 마름모까지의 길이는 92라는 것이 수상하다. x축은 범위가 10-40으로 좁고 y축 범위는 0-1000으로 넓기 때문에 y축으로 조금만 멀어져도 거리가 아주 큰 값으로 표시가 된다. 그래서 오른쪽 위 도미 샘플이 이웃으로 선택되지 못한 것.

# x축 범위를 동일하게 0-1000으로 맞춰보기 (y축 버위 지저하려면 ylim 사용)
plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D')
plt.xlim((0, 1000))
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

x와 y축 범위를 맞추니 모든 데이터가 수직으로 늘어선 형태로 바뀌었다! → 생선의 길이(x축)은 가장 가까운 이웃 찾는데 크게 영향 미치지 못함. 오로지 생선의 무게(y축)만 고려 대상이다.

두 특성(길이와 무게)의 갑이 놓인 범위가 매우 다른데 이를 두 특성의 스케일(scale)이 다르다고 말한다.

데이터를 표현하는 기준이 다르면 알고리즘 올바르게 예측할 수 없다. (특히 알고리즘 거리 기반일 땐 더더욱!) 제대로 사용하려면 특성값을 일정한 기준으로 맞춰 주어야 하낟. 이런 작업을 데이터 전처리(data preprocessing) 라 부른다.

가장 널리 사용하는 전처리 방법 중 하나는 표준점수(standard scale) 이다. (혹은 z점수) 표준 점수는 각 특성값이 평균에서 표준편차의 몇 배만큼 떨어져 있는지 나타낸다. 이를 통해 실제 특성값의 크기와 상관없이 동ㅇ리한 조건으로 비교 가능!!

mean = np.mean(train_input, axis=0)
std = np.std(train_input, axis=0)

print(mean, std)
>>> [ 27.29722222 454.09722222] [  9.98244253 323.29893931]

#표준점수 반환
train_scaled = (train_input - mean) / std

이런 넘파이 기능을 브로드캐스팅(broadcasting) 이라 부른다.

전처리 데이터로 모델 훈련하기

앞서 표준점수로 반환한 데이터로 샘플 산점도 다시 그려보기.

plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(25, 150, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

또 혼자 너무 동떨어졌다!! → 훈련 세트를 mean으로 빼고 std로 나누었기 때문에 값의 범위가 크게 달라졌다.

동일한 기준으로 다시 샘플 변경한 후 산점도 그려보기.

new = ([25, 150] - mean) / std

plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

앞서 표준편차로 변환하기 전의 산점도와 거의 동일. 크게 달라진 점은 x축과 y축의 범위가 -1.5 - 1.5 사이로 변했다는 것. 이 데이터로 다시 k-최근접 이웃 모델 훈련.

kn.fit(train_scaled, train_target)
>>> KNeighborsClassifier
    KNeighborsClassifier()

test_scaled = (test_input - mean) / std

kn.score(test_scaled, test_target)
>>> 1.0

print(kn.predict([new]))
>>> [1.]

드디어 도미(1)로 예측!
마지막으로 kneighbors() 함수로 이 샘플의 k-최근접 이웃 구한 다음 산점도 그려보자. 특성을 표준점수로 바꾸었기 때문에 k-최근접 이웃 알고리즘이 올바르게 거리 계산 했을 것!

distances, indexes = kn.kneighbors([new])
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.scatter(train_scaled[indexes,0], train_scaled[indexes,1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()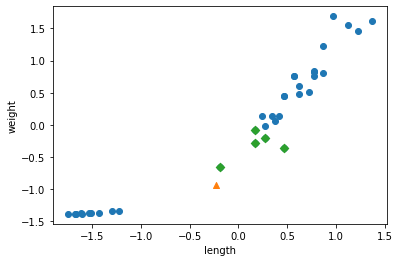

삼각형 샘플 주위 모두 도미로 성공!!

전체 코드 (출처 : https://bit.ly/hg-02-2)

fish_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 
                31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 
                35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0, 9.8, 
                10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
fish_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 
                500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 
                700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0, 6.7, 
                7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]
  
  
import numpy as np

np.column_stack(([1,2,3], [4,5,6]))

fish_data = np.column_stack((fish_length, fish_weight))

print(fish_data[:5])

print(np.ones(5))

fish_target = np.concatenate((np.ones(35), np.zeros(14)))

print(fish_target)


#사이킷런으로 훈련 세트와 테스트 세트 나누기

from sklearn.model_selection import train_test_split

train_input, test_input, train_target, test_target = train_test_split(
    fish_data, fish_target, random_state=42)
    
print(train_input.shape, test_input.shape)

print(train_target.shape, test_target.shape)

print(test_target)

train_input, test_input, train_target, test_target = train_test_split(
    fish_data, fish_target, stratify=fish_target, random_state=42)
    
print(test_target)


#수상한 도미 한마리

from sklearn.neighbors import KNeighborsClassifier

kn = KNeighborsClassifier()
kn.fit(train_input, train_target)
kn.score(test_input, test_target)

print(kn.predict([[25, 150]]))

import matplotlib.pyplot as plt

plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()


distances, indexes = kn.kneighbors([[25, 150]])


plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

print(train_input[indexes])

print(train_target[indexes])

print(distances)


#기준을 맞춰라


plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes,0], train_input[indexes,1], marker='D')
plt.xlim((0, 1000))
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

mean = np.mean(train_input, axis=0)
std = np.std(train_input, axis=0)

print(mean, std)

train_scaled = (train_input - mean) / std


#전처리 데이터로 모델 훈련하기

plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(25, 150, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

new = ([25, 150] - mean) / std

plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

kn.fit(train_scaled, train_target)

test_scaled = (test_input - mean) / std

kn.score(test_scaled, test_target)

print(kn.predict([new]))

distances, indexes = kn.kneighbors([new])

plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(new[0], new[1], marker='^')
plt.scatter(train_scaled[indexes,0], train_scaled[indexes,1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

정리

• 데이터 전처리는 머신러닝 모델에 훈련 데이터를 주입하기 전에 가공하는 단계.
• 표준점수는 훈련 세트의 스케일을 바꾸는 대표적인 방법 중 하나. 표준점수 얻으려면 특성의 평균을 빼고 표준편차로 나눔. 반드시 훈련 세트의 평균과 표준편차로 테스트 세트 바꿔야 한다.
• 브로드캐스팅은 크기가 다른 넘파이 배열에서 자동으로 사칙연산을 모든 행이나 열로 확장하여 수행하는 기능.
  
  

핵심 패키지와 함수

scikit-learn

• train_test_split() : 훈련 데이터를 훈련 세트와 테스트 세트로 나누기 전 무작위로 섞을지에 대한 여부 결정. 기본값은 True. 테스트 세트로 나눌 비율은 test_size 매개변수에서 지정할 수 있으며 기본값은 0.25
• kneighbors() : k-최근접 이웃 객체의 메서드. 입력한 데이터에 가장 가까운 이웃을 찾아 거리와 이웃 샘플의 인덱스 반환. 기본적으로 이웃의 개수는 KNeighborsClassifier 클래스의 객체를 생성할 때 지정한 개수 사용. 하지만 n_neighbors 매개변수에서 다르게 지정 가능.