20220913 (1-8)
1. Neural Networks and Deep Learning
-
신경망과 딥러닝의 기초
-
CNN (합성곱 신경망/ 주로 이미지에 적용), RNN(순환 신경망/ 조금더 복잡한, 주로 음성! 시간의 흐름에 따라 적용), LSTM 등
-
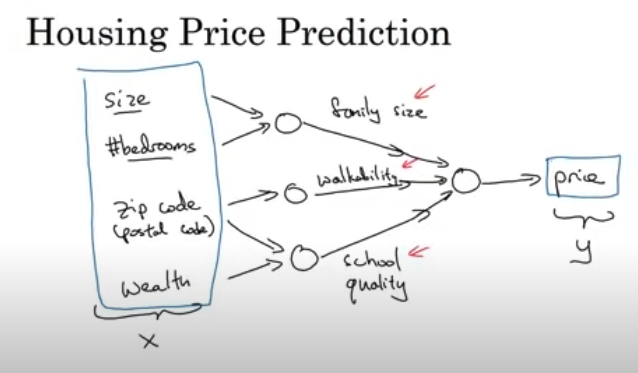
Input(x): 주택에 관한 특성들/ Output(y): 가격 Y를 예측
-
이러한 아래의 신경망을 가지고 가격 y를 예측할 것
- 각각의 원들은 신경망의 은닉 유닛
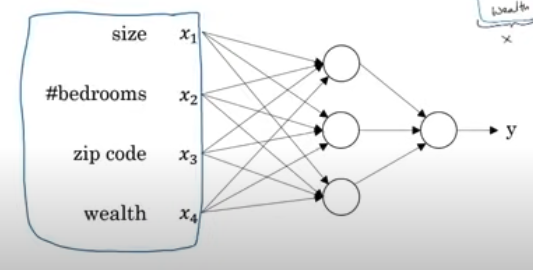
- 각각의 원들은 신경망의 은닉 유닛
-
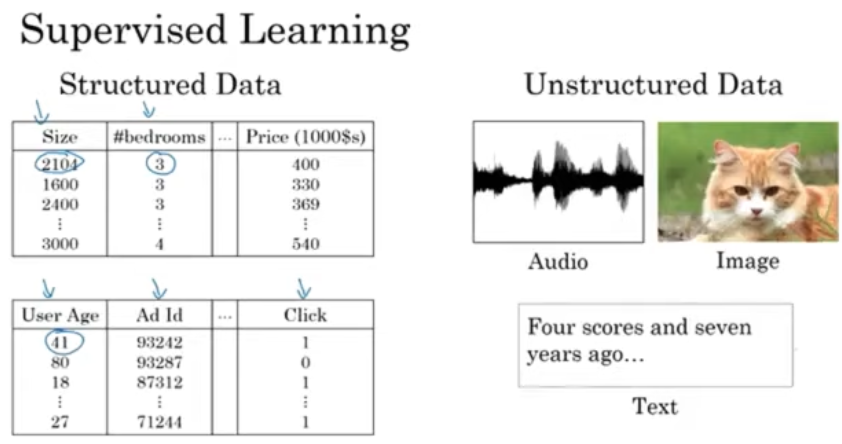
구조적 데이터, 비구조적 데이터 (해석하기 더 어려움)
[Scale drives deep learning progress]
- 규모가 큰 신경망, 데이터가 많을수록 훈련이 잘된다!
- 훈련 샘플의 크기를 나타내는 x축에 amount of data(m)사용
- data, computation, algorithms
(7. 신경망 프로그래밍의 기초)
(x,y)
- x =(n_x) x (m) 행렬/ X.shape=(nx, m)
- m이 훈련 샘플의 개수일때/ X는 m개의 열과 n_x개의 행들로 이루어져 있다.
- y의 값들을 '열'로 두는게 편하다
- y=(1) x (m) 행렬/ Y.shape=(1,m)
- y=y^(1), y^(2)....y^(m)

(8. Logistic Regression 로지스틱 회귀)
- y가 1일 확률을 잘 예측하도록 파라미터 w와 b를 학습해야 함
220914(9-)
-
매개변수들 w와 b를 학습하려면 비용함수를 정의
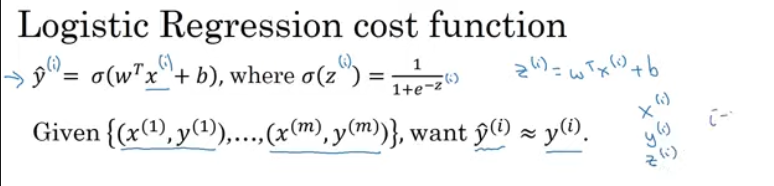
- y의 예측값은? (w의 전치)x(x) + b)의 시그모이드이며
이때 시그모이드 함수는 상단 가운데 수식처럼 정의 - 로지스틱 회귀 모델의 매개변수들 w와 b를 주어진 m개의 훈련 샘플로 학습
- 훈련세트를 바탕으로 출력한 y^(i)의 예측값이 참의 값 y^(i)에 가까워 지도록!
- (i) 위첨자의 뜻은 i-th example i번째 훈련 샘플에 관한 데이터이다!
- y의 예측값은? (w의 전치)x(x) + b)의 시그모이드이며
-
손실함수 L (Loss funtion): 출력된 y의 예측값과 참값 y 사이에 오차가 얼마나 큰지 측정
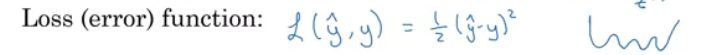
: 알고리즘이 출력한 y의 예측값과 참 값 y의 제곱 오차의 반
대신
L(^y,y) = -(y x log(y의 예측값)+(1-y)xlog(1-y)의 예측값)) 사용! -
비용(cost)함수 J(w,b): 매개변수 w와 b에 대해 손실 함수를 각각의 훈련 샘플에 적용한 값의 합들의 평균(m) 으로 나눈 값이다.
✭ 로지스틱 회귀 모델 학습이란? 손실함수 J를 최소화해주는 매개변수 (w,b)를 찾는것이다.
: '손실함수'는 하나의 훈련 샘플에 적용됨
: '비용함수'는 매개변수의 비용처럼 작용함
(10.Gradient Descent 경사 하강 알고리즘)
- 손실함수(L): 단일 훈련 샘플이 얼마나 잘 작동하는지 측정
- 비용(C)함수(J(w,b)): 매개변수 w,b가 훈련 세트 전체를 얼마나 잘 예측하는지 측정
-
Gradient Descent (로지스틱 회귀)
-
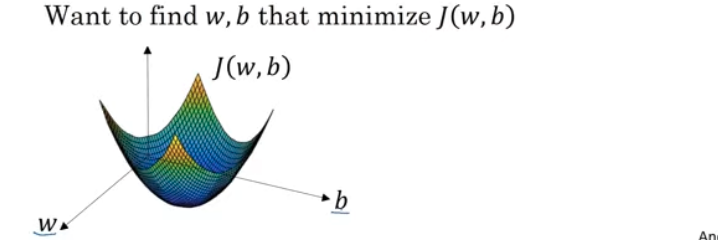
J(w,b)
- 평균으로 정의할 수 있으므로 1/m에 손실 함수의 합을 곱함
- 비용 함수를 가장 작게 만드는 w,b 찾아야 함
- 그래프의 두 가로축은 매개변수 w,b의 공간
- 곡면의 높이(비용함수) / J(w,b)
-
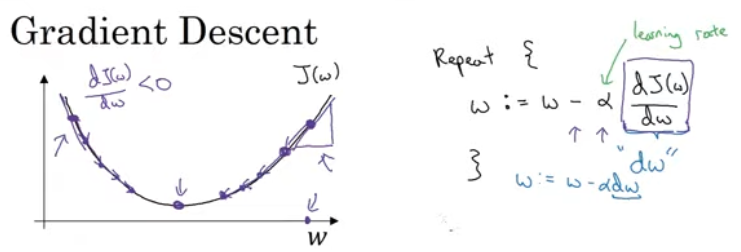
J(w)를 최소화 하기 / 경사하강법
-
(w:= 값을 갱신한다) 여기서 알파는 학습률(learning rate)

-
(1). w (w의 변화량 dw라고 씀) = w-학습률 x w에 대한 J(w,b)의 미분계수(dw) 로 갱신됨
여기서 미분계수가 양수이면 w - 미분계수 일 때 큰 수 - 작은 수 (서서히 매개변수 감소)/ 음수일 때는 (서서히 매개변수 증가) -
(2). b (b의 변화량 db라고 씀) =b-학습률 x b에대한 비용 함수의 미분계수
-
(11. Derivatives 미적분/ 도함수)

- 직삼각형의 높이/밑변의 비율은 항상 3:1
- f는 a가 오른쪽으로 민 정도보다 3배 높다! /
a=2에서 함수 f(a)의 도함수(=기울기), 미분계수는 3
- Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization
- Structuring your Machine Learning project
- Convolutional Neural Networks
- Natural Language Processing: Building sequence models