물체의 충돌 판정
https://cakelemon.tistory.com/3
https://3dev.tistory.com/53
3D 게임을 하다보면 두 물체가 서로 부딪쳤을 때나 혹은 플레이어의 캐릭터가 지형에 겹쳐서 이상하게 반응하거나 하는 경우를 볼 수 있다. 보통 이런걸 충돌판정에 대한 오류라고 우리는 인식하고 있다. 하지만 이러한 충돌 판정에 대해서 잘 생각해보진 않고 개발자들이 이 버그를 잡을 고생을 생각하며 게임을 계속할 것이다.
게임 속에 있는 물체는 각자 고유의 형태를 지니고 있다. 2D나 3D나 서로의 물체가 겹치는 상황을 원치 않는다면 두 물체들에게 충돌판정을 줘서 두 물체가 겹치지 않게 하기 위해서 특수한 알고리즘을 적용하여 두 물체의 충돌에 대한 검사를 진행한다.
가장 많이 알려진 방식으로는 AABB(Axis-Aligned Bounding Box)와 OBB(Object-Oriented Bounding Box)라는 알고리즘이다.
AABB
AABB알고리즘은 어떠한 좌표계 상에 정렬된 상태의 두 물체가 있을 때, 두 물체의 서로의 경계좌표 x, y 들을 비교해서 겹침을 확인하는 방법이다.
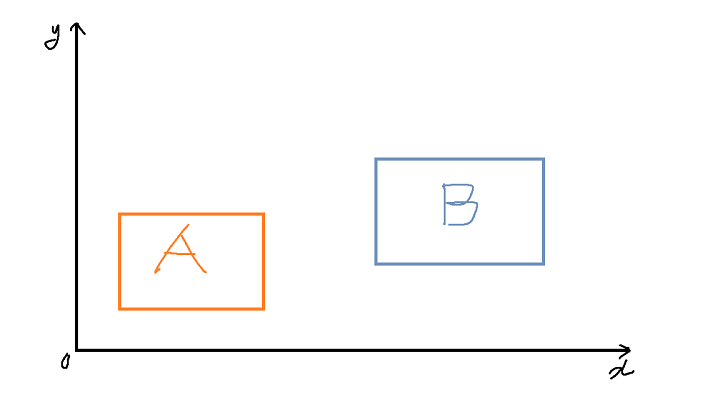
다음과 같이 두 개의 물체들의 경계선이 기준 좌표계의 축에 평행인 상태이다.
이제 두 물체가 서로에게 접근할 때, 두 물체의 경계의 기준을 정하는 좌표들을 서로 비교한다.
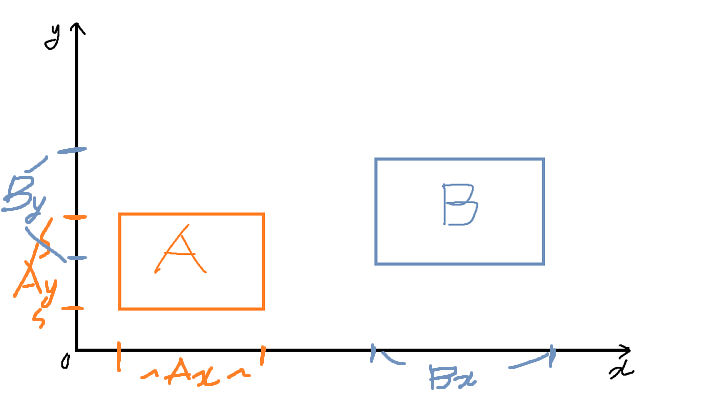
현재는 Y좌표에서 겹침이 발생하지만 X좌표의 겹침이 발생하지 않았기에 최종 충돌판정이 발생하지 않았다고 인식한다.
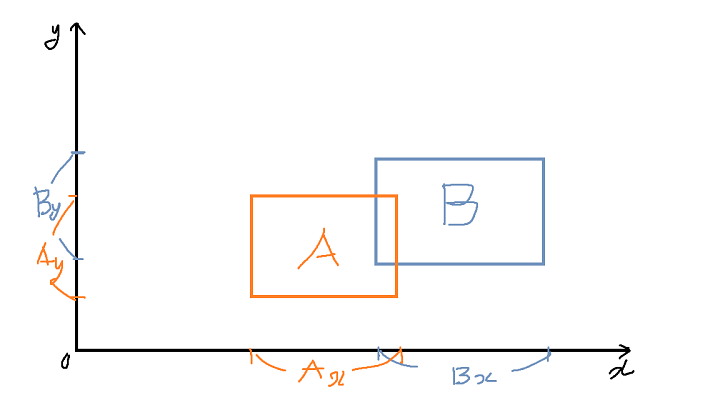
다음과 같이 X,Y 좌표가 모두 겹침이 확인되면 최종적으로 충돌판정을 일으킨다.
(코드를 통한 구현은 다음으로 미루겠다....)
AABB는 충돌판정에 대한 연산이 빠른 편이기에 자주 사용된다고한다.
좋은 예시로 격투게임인 스트리트 파이터V의 히트박스이다.
S.F.V Juri_HitBox
위 영상에서는 주리라는 캐릭터의 히트박스를 슬로우 모션으로 나타낸 것이다. 영상을 보면 히트박스가 되는 빨간박스 말고도 캐릭터들의 외각에 피격판정을 담당하는 영역도 같이 영상에 담겨있다. 속도가 중요한 격투게임에서 이 알고리즘을 사용한다는 것을 알 수 있다.
다른 게임에서는 어떻게 적용될 수 있는도 한번 생각해볼 필요가 있다.
OBB
OBB 알고리즘은 일반적으로 AABB로는 판정하기 복잡한 상황일 때 사용한다. AABB는 두 물체가 서로 정렬된 상태로 있는 상태에서 판정을 검사했다면 OBB는 물체가 회전을 하면서 물체의 축이 회전했을 때의 판정을 하기 위한 것이다.
https://kwaksh2319.tistory.com/46
http://www.gingaminga.com/Data/Note/oriented_bounding_boxes/
어쩌다가 찾은 글이다. 꽤나 자세히 잘 설명해주셔서 이해가 잘되었다.
기본적인 방법은 이러하다.
1) 각 OBB의 중심을 해당 axis에 투영한다.
2) 각 OBB가 해당 axis에 투영되었을 interval의 radius(길이의 반)을 계산한다.
3) 만일 해당 axis에 투영했을 때 OBB의 중심 사이의 거리가 각 OBB의 interval radius의 합보다 크면, 두 개의 OBB는 분리된 것으로 볼 수 있다.
라고 적혀있는데 좀 쉽게 해석해서 정리해볼 필요가 있다.
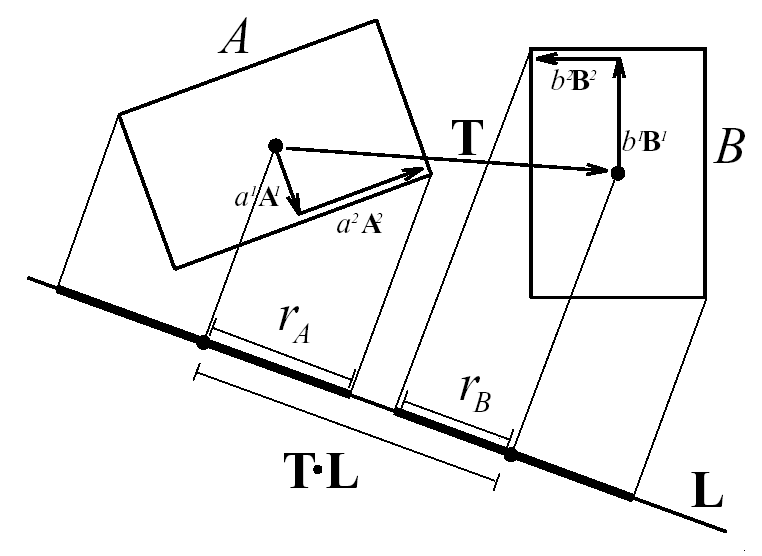
다음과 같은 상황일 때, 각 물체의 중점에서 공통된 수직 벡터(Vec.L)를 가지는 벡터를 찾은 뒤
모서리로 가는 벡터를 구하고
Vec.ra = (Vec.a1A1+ Vec.a2A2) X Vec.L (Vec.rb도 같은 방법으로)
|T X L| 의 크기가 Vec.ra와 Vec.rb의 크기보다 작으면 두 물체는 충돌했다고 판정한다.
사실 나름 이해할려고 노력해봤는데 생각보다 어려운 식이라 글을 쓰면서도 제대로 이해한건지 모르겠다.
아무튼 이 방식은 회전한 물체에 대한 충돌 판정을 진행하는 알고리즘으로 설명만큼 연산도 느려서 AABB에 비해 속도는 조금 느린 편이다. 이 방법의 경우, 제대로 판정하기 위해서는 한 축에서만 검사하는게 아니라 다른 축에서도 검사를 해야한다. 그래야 제대로된 판정이 나온다.
https://youtu.be/eED4bSkYCB8?si=9C8kFpOslcLMKzOC
유튜브에서 발견한 영상이다. 3차원은 아니지만 충돌처리에 대한 시뮬레이션을 설명할고 있다.
