트리 Tree
자료구조는 선형구조(Linear)와 비선형구조(NonLinear)로 구분된다.
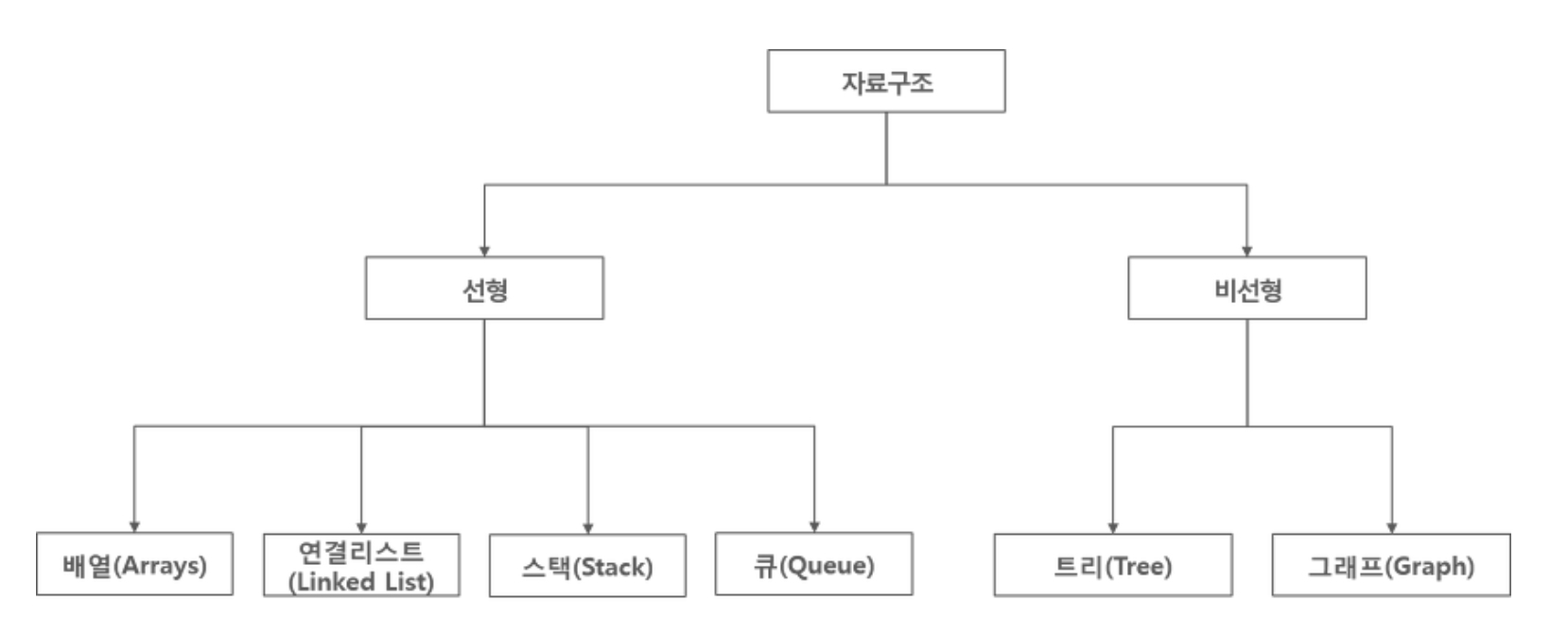
트리(Tree)란, Array, LinkedList, Stack, Queue와 같이 선형 개념의 자료구조가 아니라 부모-자식 개념을 가지는 비선형 개념의 자료구조이다.
비선형 자료구조는 하나의 자료 다음에 순차적으로 데이터가 나열되어 있는 것이 아니라 여러개의 자료가 존재할 수 있음을 의미한다.
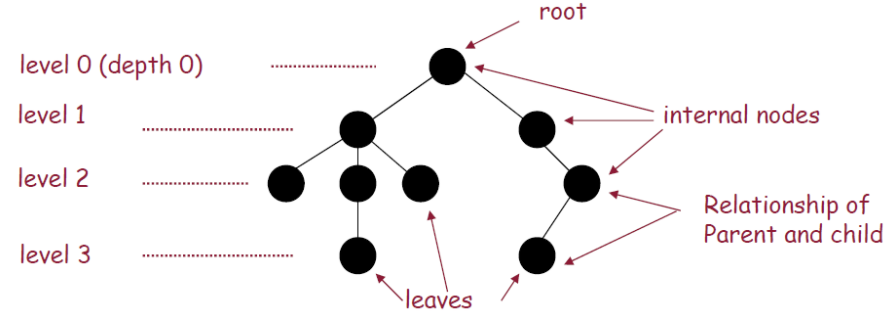
Tree 구조
이진트리 BinaryTree
트리(Tree) 중 이진트리(BinaryTree)는 컴퓨터 응용에서 가장 많이 활용되는 아주 중요한 트리구조이다.
이진트리의 중요한점은 왼쪽과 오른쪽 서브트리를 확실하게 구분한다는 것인데, 이진 트리는 모든 노드가 정확하게 두 개의 서브트리를 가지고 있다. 다만 서브트리는 공백이 될 수 있다.
노드의 유한 집합으로서 공백이거나 루트와 두 개의 분리된 이진트리인 경우 왼쪽서브트리와 오른쪽 서브트리로 구성된다.
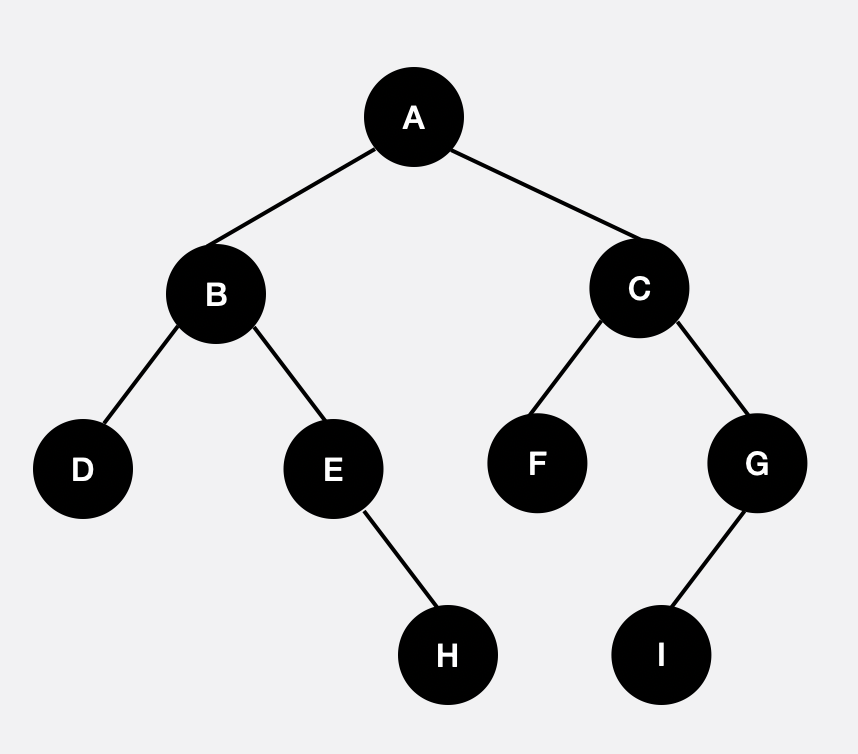
기본 Binary Tree
편향 이진트리 Skewed BinaryTree
편향 이진트리란 모든 노드가 부모의 왼쪽 자식이기 때문에 왼편으로 몰려있거나 모든 노드가 부모의 오른쪽 자식으로 되어 오른쪽으로 몰려있는 이진트리를 말한다.
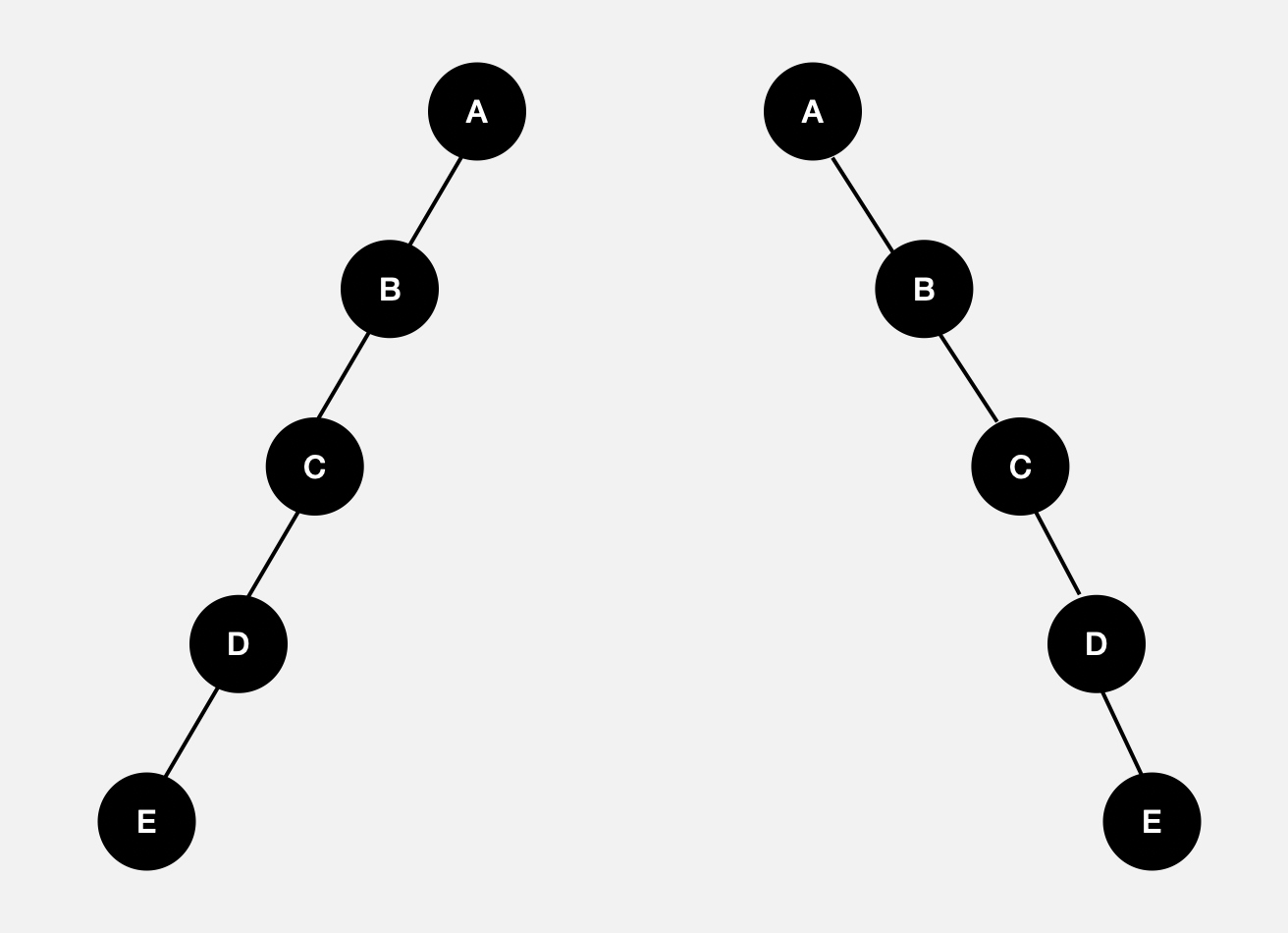
편향 이진트리
완전 이진트리 Complete BinaryTree
완전 이진 트리는 이진 트리의 조건을 만족하면서 아래 조건을 만족해야 한다.
- 마지막 높이(아래 그림에서는 높이 3)을 제외한 나머지 높이에서는 노드들이 꽉 차있어야 한다.
- 마지막 높이은 왼쪽부터 노드가 채워져 있어야 한다.
만일 높이가 h(root 높이 : 0)이고 노드 수가 n 일 때, n<=( 2^h -1 )인 이진트리를 노드의 레벨 순수에 따라 노드 번호를 붙인다면 이때 각 노드 번호의 위치가 포화 이진트리 번호 1에서 n까지의 위치와 모두 정확하게 일치한다면(조건2를 충족) 이 트리를 완전 이진트리라고 한다.
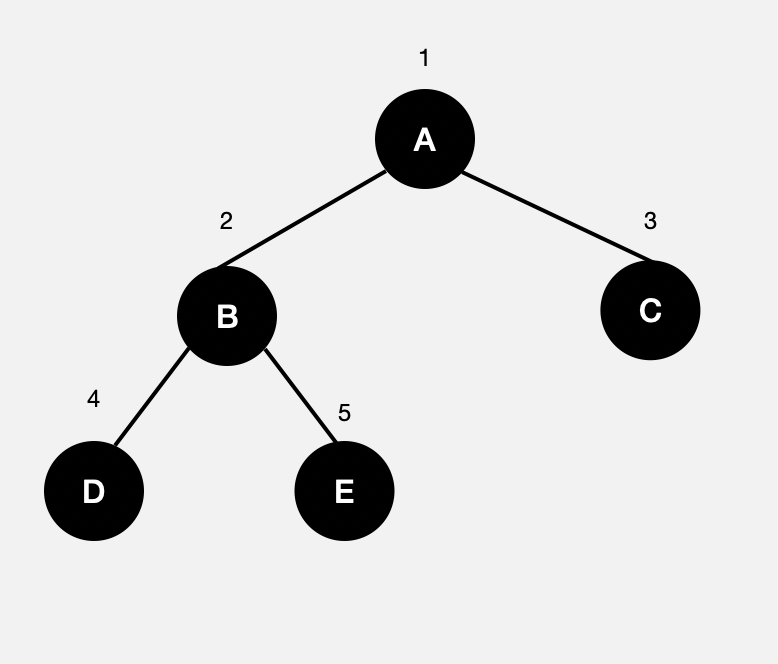
완전 이진트리
n <= 7(2^3-1), n =5으로 충족하고 높이 2까지 노드가 꽉차있고 높이 3에서는 왼쪽부터 노드가 채워져있으므로 해당 트리는 완전 이진트리이다.
포화 이진트리 Full BinaryTree
포화 이진트리는 이진 트리의 조건을 만족하면서 아래 조건을 만족해야 한다.
1. 루트 노드를 제외한 모든 노드들은 2개의 자식 노드를 가지거나 자식 노드가 하나도 없어야 한다.
포화 이진트리란 이진트리가 보유할 수 있는 최대의 노드를 가지고 있는 형태이다. 높이가 h인 이진 트리에서 있을 수 있는 최대 노드 수는 2^h -1 이다. 아래 그림은 높이가 3인 포화 이진트리이다.
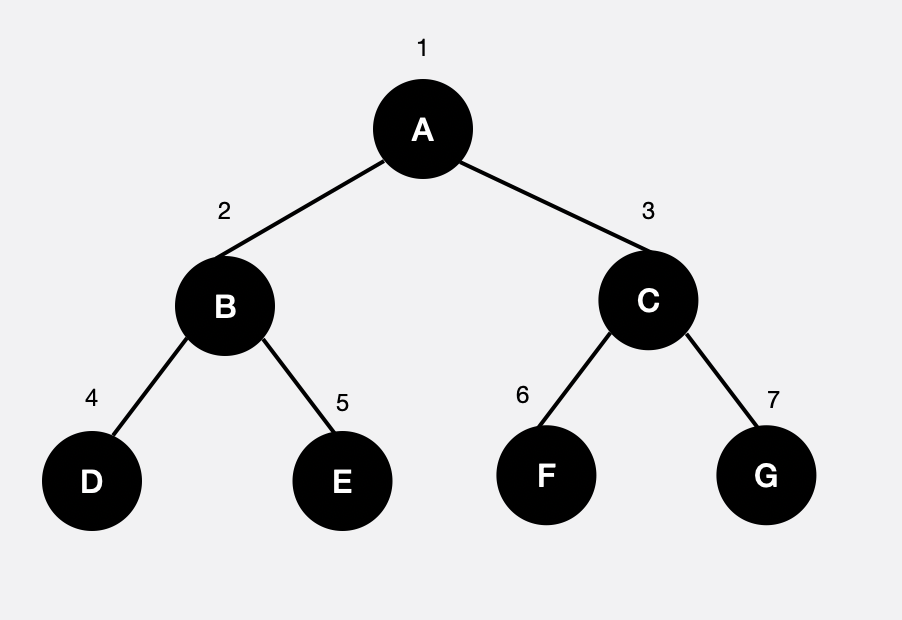
포화 이진트리
이진트리 연결 표현
Array 1차원 배열로 순차적으로 데이터를 쉽게 표현할 수 있지만, 편향 이진트리와 같은 데이터를 저장할 때에는 저장공간을 효율적으로 사용하지 못한다는 단점을 가지고 있다.
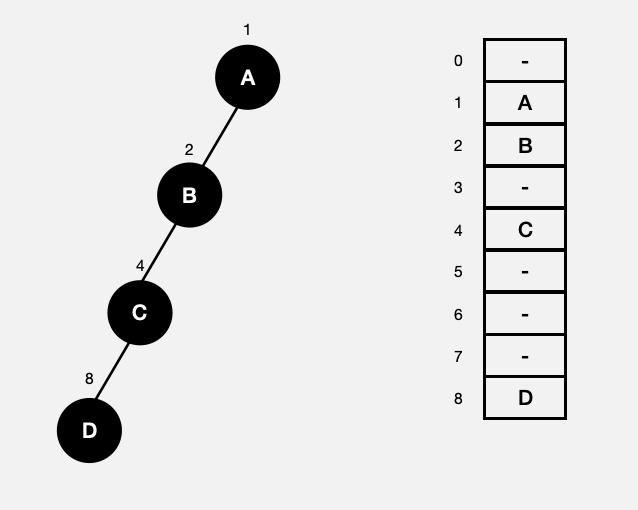
BinaryTree Array 순차표현
그러한 단점을 커버하고자 다음 레벨의 데이터를 가리키는 left, right 포인터를 가지고 있는 노드를 사용하여 연결표현을 나타낸다.
이 노드 구조는 부모 노드를 찾기가 어렵다는 문제점이 있지만 꼭 필요한 경우에는 parent필드를 추가해서 사용하면 된다.
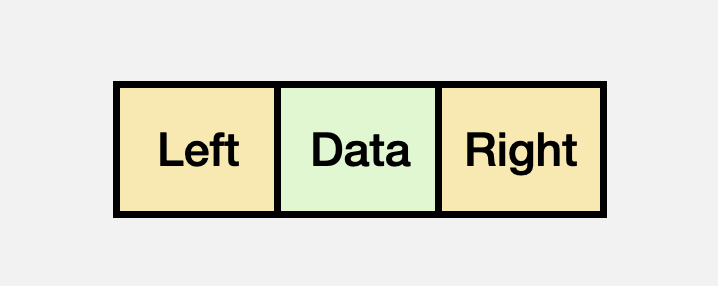
BinaryTree Node구조
완전이진트리를 Node로 표현하여 나타내면 다음 그림과 같다. 만약 서브트리가 없다면 각 left, right의 데이터는 null이 된다.
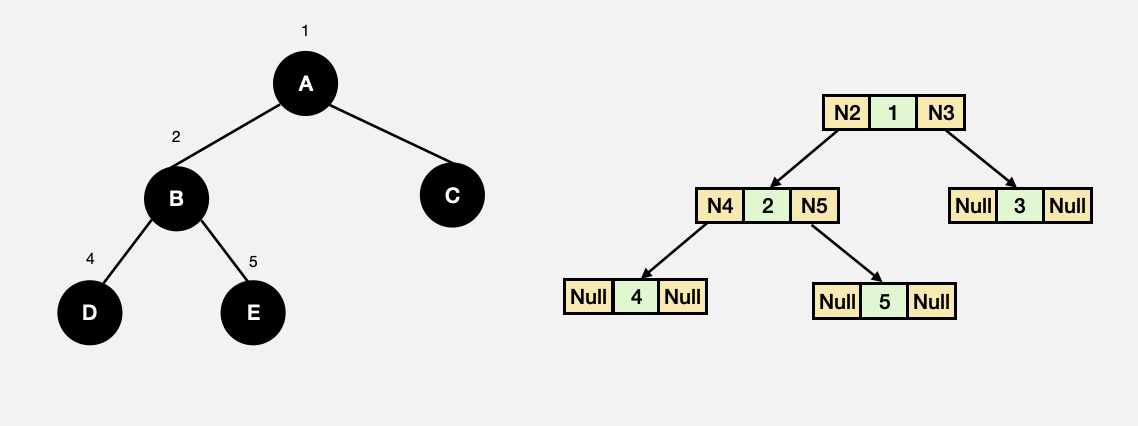
BinaryTree Node 연결 표현
BinaryTree 구현코드
Node.java
package com.example.study.livestudy.week4.BinaryTree;
/**
* BinaryTree Node
*/
public class Node {
private int value;
private Node left;
private Node right;
public Node(){
}
public Node(int value, Node left, Node right){
this.left = left;
this.right = right;
this.value = value;
}
public int getValue() {
return value;
}
public Node getLeft() {
return left;
}
public Node getRight() {
return right;
}
}
BinaryTree.java
package com.example.study.livestudy.week4.BinaryTree;
import java.util.LinkedList;
import java.util.Queue;
public class BinaryTree {
private Node root;
public BinaryTree(Node root){
this.root = root;
}
public Node getRoot(){
return root;
}
/**
* BFS
*/
public void printByBFS(Node root){
Queue<Node> q = new LinkedList<>();
q.offer(root);
while(!q.isEmpty()){
Node next = q.poll();
System.out.print(next.getValue()+" ");
if(next.getLeft() != null){
q.offer(next.getLeft());
}
if(next.getRight() != null){
q.offer(next.getRight());
}
}
System.out.println();
}
/**
* DFS
* 왼쪽, 루트, 오른쪽 순으로 순회
*/
public void printByDFS(Node root){
if(root == null) return;
printByDFS(root.getLeft());
System.out.print(root.getValue()+" ");
printByDFS(root.getRight());
}
public static void main(String[] args) {
Node node10 = new Node(10,null,null);
Node node9 = new Node(9,null,null);
Node node8 = new Node(8,node10,null);
Node node7 = new Node(7,null,node9);
Node node6 = new Node(6,node8,null);
Node node5 = new Node(5,null,null);
Node node4= new Node(4,node7,null);
Node node3 = new Node(3,node5,node6);
Node node2 = new Node(2,node4,null);
Node node1 = new Node(1,node2,node3);
BinaryTree binaryTree = new BinaryTree(node1);
Node root = binaryTree.getRoot();
System.out.println("root : " + root.getValue());
System.out.println();
System.out.println("===== BFS =====");
binaryTree.printByBFS(root);
System.out.println();
System.out.println("===== DFS =====");
binaryTree.printByDFS(root);
}
}
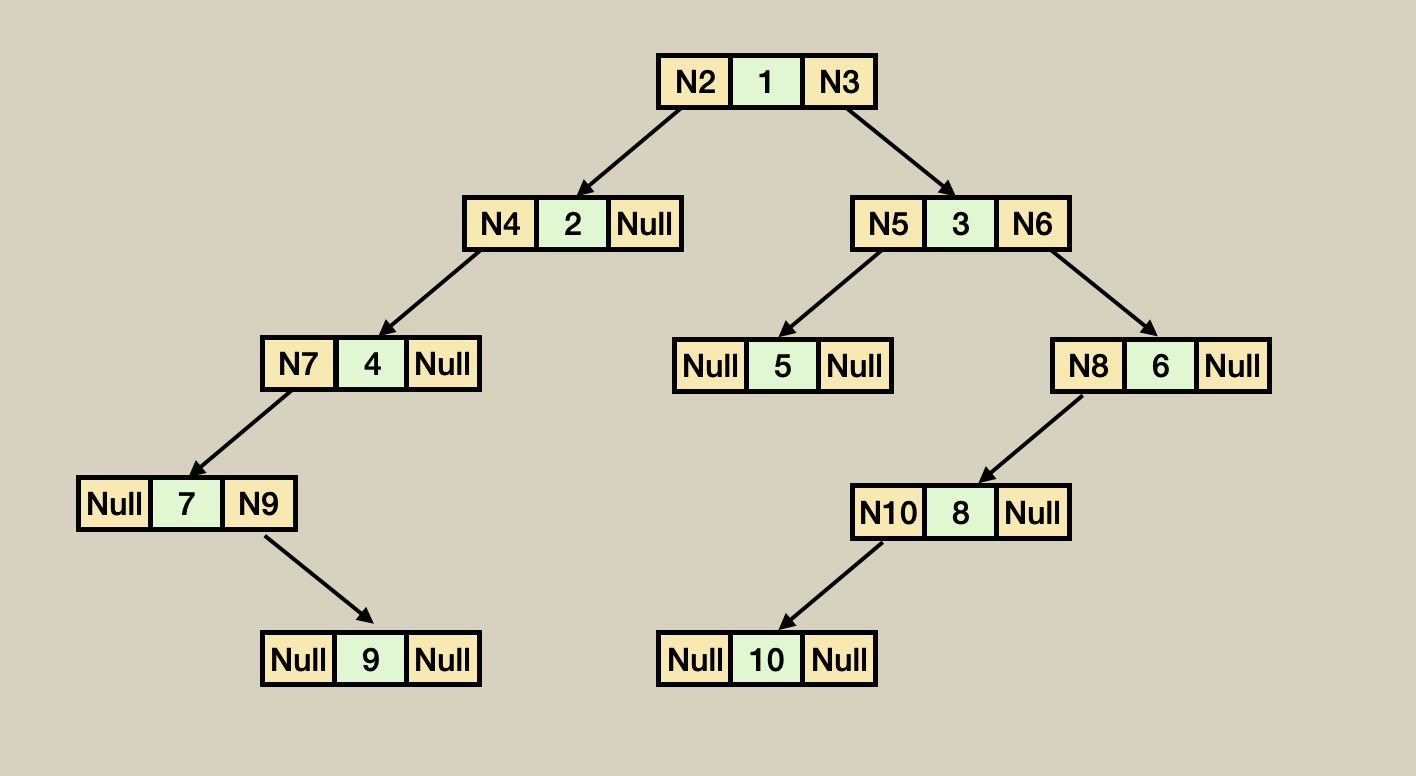
BinaryTree Node 연결 표현
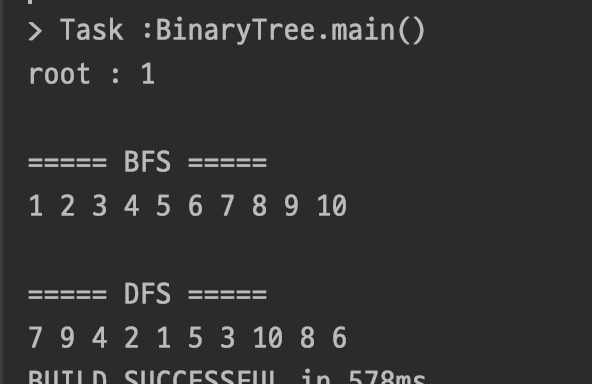
위의 이진트리 코드를 BFS, DFS탐색방식으로 구하면 다음 결과와 같다
테스트 결과