1. 트리(Tree) 구조
- 트리 : Node 와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
- 실제로 어디에 많이 사용되나?
- 트리 중 이진 트리 (Binary Tree)형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨
2. 알아둘 용어
- Node : 트리에서 데이터를 저장하는 기본 요소(데이터와 다른 연결된 노드에 대한 Branch정보 포함)
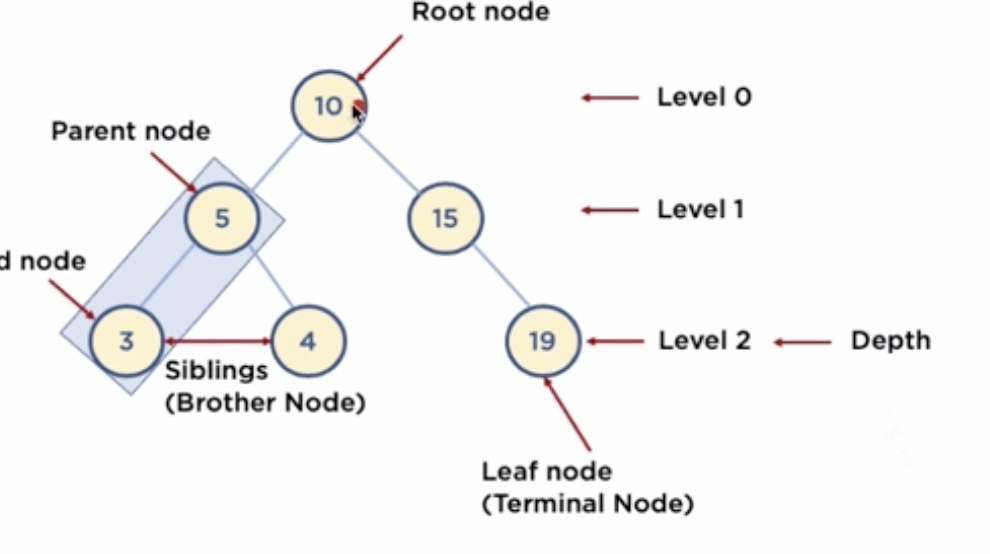
- Root Node : 트리 맨 위에있는 노드
- Level : 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node : 어떤 노드의 다음 레벨에 연결된 노드
- Child Node : 어떤 노드의 상위 레벨에 연결된 노드
- Leaf Node (Terminal Node) : Child Node 가 하나도 없는 노드
- Sibling (Brother Node) : 동일한 Parent Node를 가진 노드
- Depth : 트리에서 Node가 가질 수 있는 최대 Level
3. 이진 트리와 이진 탐색 트리 (Binary Search Tree)
- 이진 트리 : 노드의 최대 Branch가 2 인 트리
- 이진 탐색 트리 (BInary Search Tree, BST) : 이진 트리에 다음과 같은 추가적인 조건이 있는 트리
- 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있음

4. 자료 구조 이진 탐색 트리의 장점과 주요 용도
- 주요 용도 : 데이터 검색 (탐색)
- 장점 : 탐색 속도를 개선할 수 있음
이진 트리와 정렬된 배열간의 탐색 비교

import java.util.*;
class Node<T>{
private T element;
private Node<T> parent;
private Node<T> left;
private Node<T> right;
Node(T element){
this.element = element;
this.parent = null;
this.left = null;
this.right = null;
}
Node(T element, Node<T> left, Node<T> right){
this.element = element;
this.parent = null;
this.left = left;
this.right = right;
}
Node<T> setParent(Node<T> parent){
this.parent = parent;
return this;
}
T getElement() {return this.element;}
Node<T> setElement(T element){this.element = element; return this;}
Node<T> getLeft(){
return this.left;
}
Node<T> setLeft(Node<T> left){
this.left = left;
return this;
}
Node<T> getRight(){
return this.right;
}
Node<T> setRight(Node<T> right){
this.right = right;
return this;
}
Node<T> getParent(){
return this.parent;
}
}
class Tree<T> {
private Node<T> root;
private int size;
public Tree(){
this(null);
}
public Tree(Node<T> root){
this.root = root;
if (root != null){
size = 1;
}
}
public int size(){
return this.size;
}
public Node<T> getRoot(){
return this.root;
}
public Tree<T> setRoot(T element){
if (root == null)
size = 1;
this.root = new Node(element);
return this;
}
public Node<T> addLeft(Node<T> parent, Node<T> child){
if (parent.getLeft() != null){
System.out.println("Already have left");
return null;
}
size++;
parent.setLeft(child);
return parent;
}
public Node<T> addRight(Node<T> parent, Node<T> child){
if (parent.getRight() != null){
System.out.println("Aready have right");
return null;
}
size++;
parent.setRight(child);
return parent;
}
public Node<T> removeLeft(Node<T> parent){
Node<T> target = parent.getLeft();
if (target != null)
size--;
parent.setLeft(null);
return target;
}
public Node<T> removeRight(Node<T> parent){
Node<T> target = parent.getRight();
if (target != null)
size--;
parent.setRight(null);
return target;
}
public void preorder(Node<T> node){
System.out.println(node.getElement());
if (node.getLeft() != null){
preorder(node.getLeft());
}
if (node.getRight() != null){
preorder(node.getRight());
}
}
public void inorder(Node<T> node){
if (node.getLeft() != null){
inorder(node.getLeft());
}
System.out.println(node.getElement());
if (node.getRight() != null){
inorder(node.getRight());
}
}
public void postorder(Node<T> node){
if (node.getLeft() != null){
postorder(node.getLeft());
}
if (node.getRight() != null){
postorder(node.getRight());
}
System.out.println(node.getElement());
}
}
public class HelloWorld{
public static void main(String []args){
Tree<String> tree = new Tree(new Node("A"));
Node<String> root = tree.getRoot();
tree.addLeft(root, new Node("B"));
tree.addRight(root, new Node("I"));
tree.addLeft(root.getLeft(), new Node("C"));
tree.addRight(root.getLeft(), new Node("F"));
tree.addLeft(root.getRight(), new Node("J"));
tree.addRight(root.getRight(), new Node("M"));
System.out.println("=====preorder=====");
tree.preorder(root);
System.out.println("\n=====inorder=====");
tree.inorder(root);
System.out.println("\n=====postorder=====");
tree.postorder(root);
System.out.println("\ntree size : " + tree.size());
System.out.println("=======remove root.right.left====");
tree.removeLeft(root.getRight());
tree.preorder(root);
System.out.println("\ntree size : " + tree.size());
}
}=====inorder=====
C
B
F
A
J
I
M
=====postorder=====
C
F
B
J
M
I
A
tree size : 7
=======remove root.right.left====
A
B
C
F
I
M
tree size : 6
5. 트리 노드 삭제
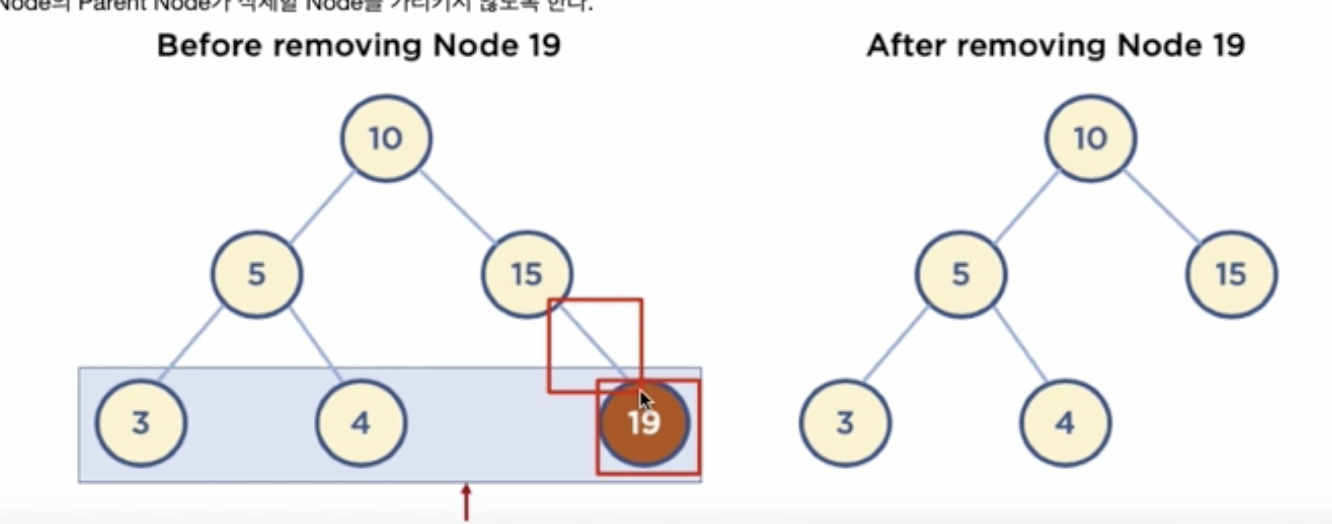
5.1 Leaf Node 삭제
- Leaf Node : Child Node 가 없는 Node
- 삭제할 Node의 Parent Node가 삭제할 Node를 가리키지 않도록 한다.
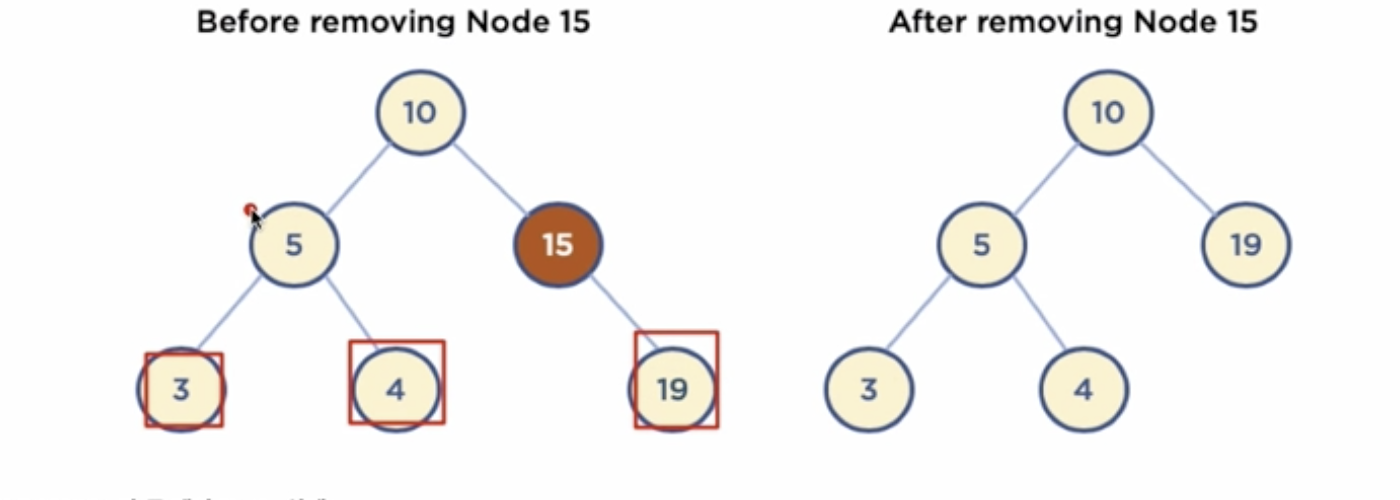
5.2 Child Node가 하나인 Node 삭제
- 삭제할 Node의 Parent Node가 삭제할 Node의 Child Node를 가리키도록 한다.
5.3 Child Node 가 두 개인 Node 삭제
- 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
- 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
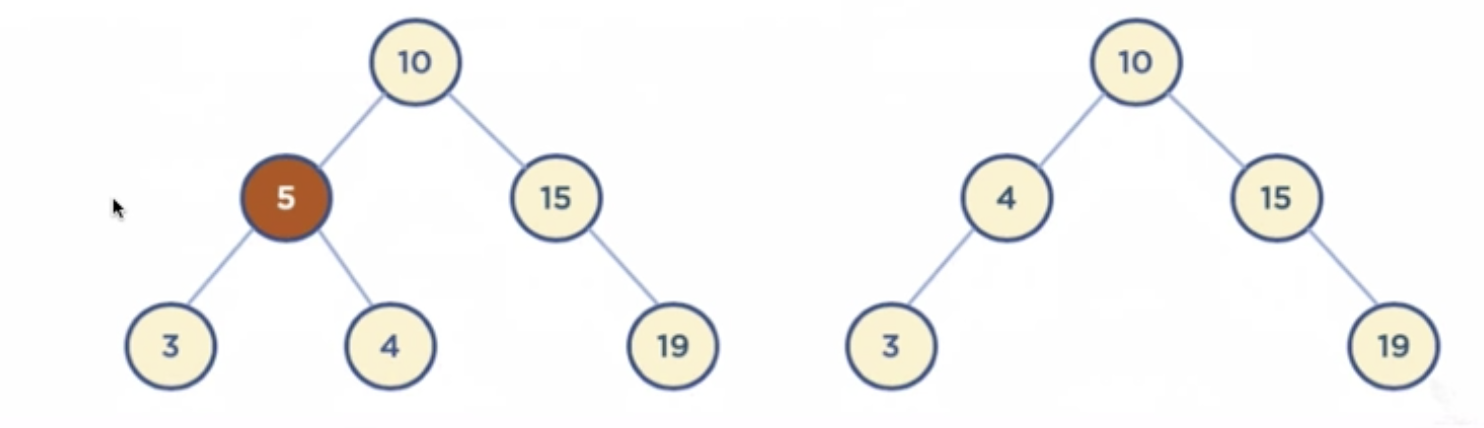
삭제할 Node의 오른쪽 자식중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키게 할 경우
- 삭제할 Node의 오른쪽 자식 선택
- 오른쪽 자식의 가장 왼쪽에 있는 Node를 선택
- 해당 Node를 삭제할 Node의 Parent Node의 왼쪽 Branch가 가리키게 함
- 해당 Node의 왼쪽 Branch가 삭제할 Node의 왼쪽 Child Node를 가리키게 함
- 해당 Node의 오른쪽 Branch가 삭제할 Node의 오른쪽 Child Node를 가리키게 함
- 만약 해당 Node가 오른쪽 Child Node를 가지고 있었을 경우에는, 해당 Node의 본래 Parent Node의 왼쪽 Branch가 해당 오른쪽 Child Node를 가리키게 함
package treedatastructure;
import java.util.*;
class Node {
int value;
Node leftChild;
Node rightChild;
public Node(int value) {
this.value = value;
this.leftChild = null;
this.rightChild = null;
}
}
class BinaryTree {
Node rootNode = null;
/**
* 새로운 노드 삽입
*/
public void insertNode(int element) {
/*
* 루트가 빈 경우, 즉 아무 노드도 없는 경우
*/
if (rootNode == null) {
rootNode = new Node(element);
} else {
Node head = rootNode;
Node currentNode;
while (true) {
currentNode = head;
/*
* 현재의 루트보다 작은 경우, 왼쪽으로 탐색을 한다.
*/
if (head.value > element) {
head = head.leftChild;
/*
* 왼쪽 자식 노드가 비어있는 경우, 해당 위치에 추가할 노드를 삽입한다.
* 현재 currenNode head를 가리키고 있다.
*/
if (head == null) {
currentNode.leftChild = new Node(element);
break;
}
} else {
/*
* 현재의 루트보다 큰 경우, 오른쪽으로 탐색을 한다.
*/
head = head.rightChild;
/*
* 오른쪽 자식 노드가 비어있는 경우, 해당 위치에 추가할 노드를 삽입한다.
* 현재 currenNode head를 가리키고 있다.
*/
if (head == null) {
currentNode.rightChild = new Node(element);
break;
}
}
}
}
}
/**
* 특정 노드 삭제
*/
public boolean removeNode(int element) {
Node removeNode = rootNode;
Node parentOfRemoveNode = null;
while (removeNode.value != element) {
parentOfRemoveNode = removeNode;
/* 삭제할 값이 현재 노드보다 작으면 왼쪽을 탐색한다. */
if (removeNode.value > element) {
removeNode = removeNode.leftChild;
} else {
removeNode = removeNode.rightChild;
}
/*
* 값 대소를 비교하며 탐색했을 때
* 잎 노드(Leaf node)인 경우 삭제를 위한 탐색 실패
*/
if (removeNode == null)
return false;
}
/* 자식 노드가 모두 없을 때 */
if (removeNode.leftChild == null && removeNode.rightChild == null) {
/* 삭제 대상이 트리의 루트일 때 */
if (removeNode == rootNode) {
rootNode = null;
} else if (removeNode == parentOfRemoveNode.rightChild) {
parentOfRemoveNode.rightChild = null;
} else {
parentOfRemoveNode.leftChild = null;
}
}
/* 오른쪽 자식 노드만 존재하는 경우 */
else if (removeNode.leftChild == null) {
if (removeNode == rootNode) {
rootNode = removeNode.rightChild;
} else if (removeNode == parentOfRemoveNode.rightChild) {
/*
* 삭제 대상의 오른쪽 자식 노드를 삭제 대상 위치에 둔다.
*/
parentOfRemoveNode.rightChild = removeNode.rightChild;
} else {
parentOfRemoveNode.leftChild = removeNode.rightChild;
}
}
/* 왼쪽 자식 노드만 존재하는 경우 */
else if (removeNode.rightChild == null) {
if (removeNode == rootNode) {
rootNode = removeNode.leftChild;
} else if (removeNode == parentOfRemoveNode.rightChild) {
parentOfRemoveNode.rightChild = removeNode.leftChild;
} else {
/*
* 삭제 대상의 왼쪽 자식을 삭제 대상 위치에 둔다.
*/
parentOfRemoveNode.leftChild = removeNode.leftChild;
}
}
/*
* 두 개의 자식 노드가 존재하는 경우
* 삭제할 노드의 왼쪽 서브 트리에 있는 가장 큰 값 노드를 올리거나
* 오른쪽 서브 트리에 있는 가장 작은 값 노드를 올리면 된다.
* 구현 코드는 2번째 방법을 사용한다.
*/
else {
/* 삭제 대상 노드의 자식 노드 중에서 대체될 노드(replaceNode)를 찾는다. */
Node parentOfReplaceNode = removeNode;
/* 삭제 대상의 오른쪽 서브 트리 탐색 지정 */
Node replaceNode = parentOfReplaceNode.rightChild;
while (replaceNode.leftChild != null) {
/* 가장 작은 값을 찾기 위해 왼쪽 자식 노드로 탐색한다. */
parentOfReplaceNode = replaceNode;
replaceNode = replaceNode.leftChild;
}
if (replaceNode != removeNode.rightChild) {
/* 가장 작은 값을 선택하기 때문에 대체 노드의 왼쪽 자식은 빈 노드가 된다. */
parentOfReplaceNode.leftChild = replaceNode.rightChild;
/* 대체할 노드의 오른쪽 자식 노드를 삭제할 노드의 오른쪽으로 지정한다. */
replaceNode.rightChild = removeNode.rightChild;
}
/* 삭제할 노드가 루트 노드인 경우 대체할 노드로 바꾼다. */
if (removeNode == rootNode) {
rootNode = replaceNode;
} else if (removeNode == parentOfRemoveNode.rightChild) {
parentOfRemoveNode.rightChild = replaceNode;
} else {
parentOfRemoveNode.leftChild = replaceNode;
}
/* 삭제 대상 노드의 왼쪽 자식을 잇는다. */
replaceNode.leftChild = removeNode.leftChild;
}
return true;
}
/**
* 중위 순회
*/
public void inorderTree(Node root, int depth) {
if (root != null) {
inorderTree(root.leftChild, depth + 1);
for (int i = 0; i < depth; i++) {
System.out.print("ㄴ");
}
System.out.println(root.value);
inorderTree(root.rightChild, depth + 1);
}
}
/**
* 후위 순회
*/
public void postorderTree(Node root, int depth) {
if (root != null) {
postorderTree(root.leftChild, depth + 1);
postorderTree(root.rightChild, depth + 1);
for (int i = 0; i < depth; i++) {
System.out.print("ㄴ");
}
System.out.println(root.value);
}
}
/**
* 전위 순회
*/
public void preorderTree(Node root, int depth) {
if (root != null) {
for (int i = 0; i < depth; i++) {
System.out.print("ㄴ");
}
System.out.println(root.value);
preorderTree(root.leftChild, depth + 1);
preorderTree(root.rightChild, depth + 1);
}
}
}
public class TreeMapInJava{
public static void main(String []args){
BinaryTree tree = new BinaryTree();
tree.insertNode(5);
tree.insertNode(8);
tree.insertNode(7);
tree.insertNode(10);
tree.insertNode(9);
tree.insertNode(11);
if (tree.removeNode(10)) {
System.out.println("노드 삭제");
}
// tree.inorderTree(tree.rootNode, 0);
// tree.postorderTree(tree.rootNode, 0);
tree.preorderTree(tree.rootNode, 0);
}
}