시계열분석 - ARIMA 모델

쏜·2021년 9월 5일

시계열

Youtube 김성범 교수님의 ARIMA 모델 개요 - Part 1,2 강의영상을 보고 정리한 내용입니다.

Stationary Process (정상 프로세스)

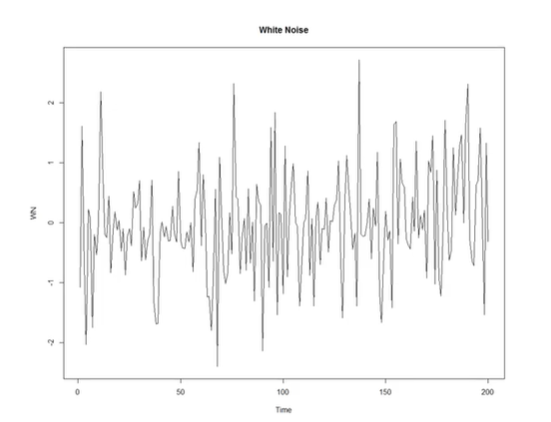
정상 프로세스 : 시간에 관계없이 평균과 분산이 일정한 시계열 데이터

정상성 확인 (Autocorrelation Function의 패턴을 이용해서)

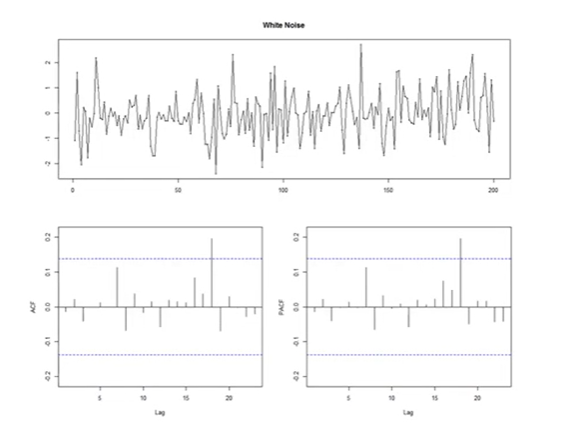
맨 위의 그림을 보면 평균이랑 분산이 일정하다는 것을 쉽게 눈으로 판단할 수 있지만 복잡한 데이터인 경우엔 그래프로 판단하기 어려울 수 있다.

=> 내가 분석하고자 하는 데이터가 stationary인지 아닌지를 확인해 볼 수 있는 방법은?

1. ACF (Autocorrelation Function)
=> 아래에서 왼쪽 그래프 참고 (x축은 lag, y축은 ACF)

lag=1이라는 건?
: 한 시점 미룬 데이터와의 차이를 의미
자기 자신과 자기 자신 이전 데이터와의 correlation = Autocorrelation lag 1이다.
그럼 lag=2는?
: 자신 자신 데이터와 두 시점 미룬 데이터와의 correlation = Autocorrelation lag 2
lag=20일 때는?
: 현재 데이터와 20 시점을 shift한 데이터와의 correlation = Autocorrelation lag 20

이 그래프에서는 5시점 shift한 것과 autocorrelation이 꽤 있는 것으로 보임

2. PACF (Partial Autocorrelation Function)

추후에 설명 예정

일단 데이터를 받았을 때, stationary인지 확인하려면 ACF 그래프를 그려보고 판단할 수 있다. 하지만 이것도 그림이기 때문에 주관적인 요소는 들어간다.

Nonstationary Process (비정상 프로세스)

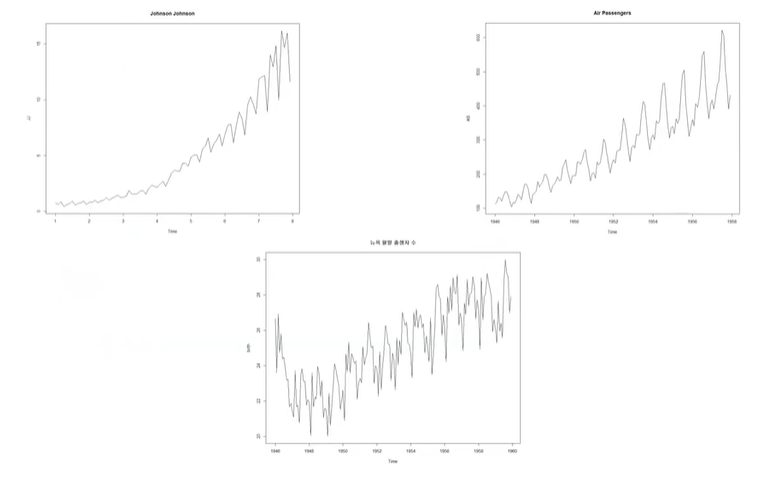
정상 프로세스와 반대로 시간에 따라 분산이나 평균이 일정하지 않은 경우이다.

첫번째 데이터는 쭉 올라가는 모양이다. 따라서 평균도 바뀌고 분산도 처음에는 작다가 뒤로 갈수록 커지는 걸 볼 수 있다.

두번째 데이터도 역시 평균이 올라가고 분산도 초반에 비해 최근이 커지는 경향을 볼 수 있다.

세번째 데이터는 초반에 줄어들다가 올라가는 모습으로 평균이 일정하지 않고 분산은 일정하다고 볼 수 있다.

비정상성 확인 (Autocorrelation Function의 패턴을 이용해서)

예제 1)

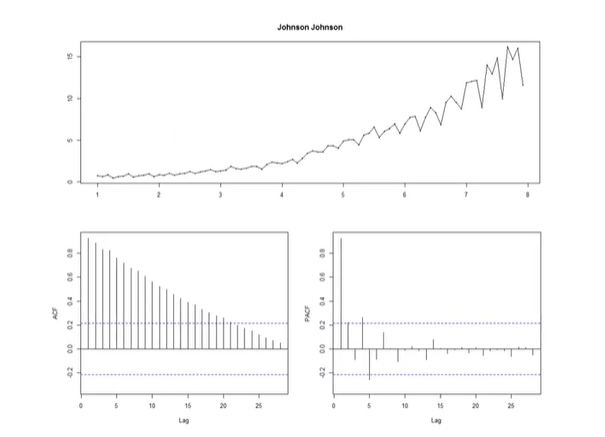
위의 데이터의 autocorrelation을 나타낸 것이 아래의 왼쪽 그래프이다. Nonstationary인 경우에 autocorrelation을 찍어보면 왼쪽 그래프와 같이 천천히 줄어드는 모습이다.

예제 2)

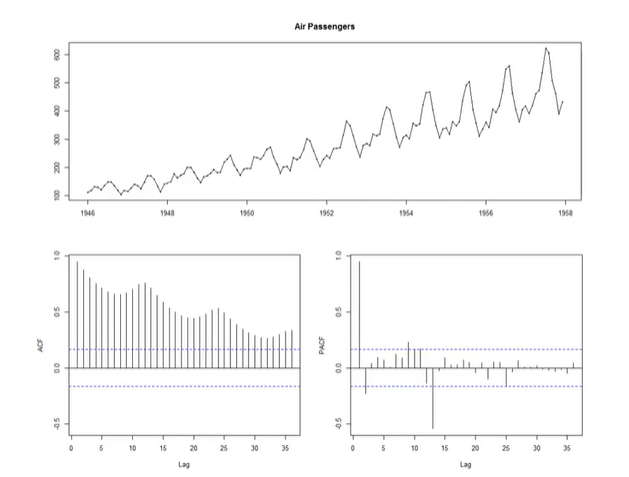
air passenger 데이터이다. 증가하는 경향이 보이고 분산도 바뀌는 대표적인 nonstationary 이다. autocorrelation을 찍어보면 떨어졌다 올라갔다하지만 전반적으로 떨어지는 패턴을 보인다. 이런 패턴 역시 nonstationary에서 볼 수 있는 패턴이다

< ACF를 통해서 정상성을 알아보는 방법 정리 >

일정한 패턴이 없거나 갑자기 떨어지는 패턴 => stationary
일정하게 떨어지거나 올라갔다 내려갔다하면서 굉장히 천천히 떨어지는 패턴 => nonstationary

Autoregressive (AR) Models

dependent variable인 Y의 lag를 independent variables인 X로 사용하는 모델

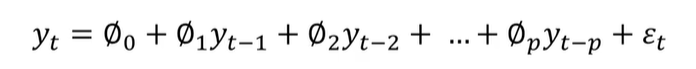
첫번째 X가 바로 $y_{t-1}$ , 즉 y의 한 시점전 데이터, $y_{t-2}$ 는 두 시점 전 데이터,..., $y_{t-p}$ 는 p 시점 전 데이터를 의미한다.
자기자신을 X로 삼기때문에 $X_1$ = $y_{t-1}$ , $X_2$ = $y_{t-2}$ ,.., $X_p$ = $y_{t-p}$ 로 생각하면 된다.
$\phi_0$ 는 인털셉
$y_t$ 를 모델링할 때 $y_t$ 의 lag된 변수들(자신의 과거 데이터)을 X 삼아서 회귀모델을 만듦 .(Auto = self라고 생각하면 됨)

multiple regression model과 다른 점

자기자신을 갖고 모델링을 하기 때문에 독립성이 없다.
$\phi_0$ (계수)를 추정할 때 일반적으로 사용했던 최소제곱법은 사용할 수 없다.

Moving Average (MA) Models

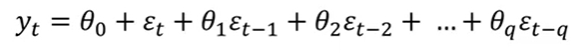
$y_t$ 를 $\varepsilon$ (엡실론=error)으로 모델링
t시점의 데이터( $y_t$ )를 t 시점의 에러( $\varepsilon_t$ )와 과거의 에러들로 표현
연속적인 에러 term으로 y와d의 관계를 모델링하는 방법

Autoregressive and Moving Average (ARMA)

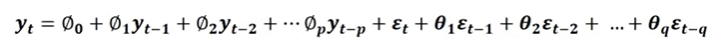
AR과 MA을 합친 모델
t시점의 데이터( $y_t$ )를 자기자신의 lag된 값들, t시점의 error와 전 시점의 error들로 표현함

AR, MA, ARMA 이 모델들을 구현하기 위해서는 분석해야되는 데이터가 stationary해야된다. nonstationary인 경우, 이 모델들을 적용할 수 없다.

일상생활엔 nonstationary한 데이터들이 훨씬 더 많다. 따라서 stationary한 데이터로 바꾼 뒤에 이 모델링을 할 수 있다.

어떻게 nonstationary를 stationary로 바꿀까?
=>가장 간단한 방법이 바로 differencing(차분) !

Autoregressive Integrated Moving Average (ARIMA)

differencing을 했다는 것을 "integrated"로 표현함
I라는 것은 differencing을 몇번 했는지를 의미
AR -> p, I -> d, MA -> q (p,d,q)
AR모델에서 p = independent variable의 개수를 나타냄
MR모델에서 q, $\theta$ 의 개수, 즉 파라미터의 개수를 나타냄
d = 몇번 differencing을 했냐

차분 (Differencing)

original 데이터가 nonstationary인 경우, 차분이 필요할 것이다.
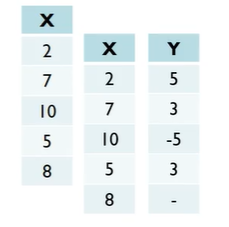
원래 데이터와 원래 데이터를 한번 shift한 것을 빼주면 결과가 나오는데 이것이 바로 첫번째 differencing한 결과이다.
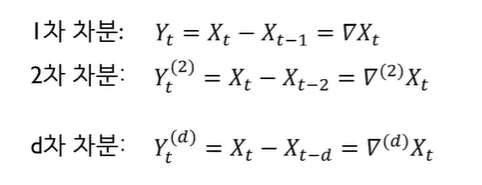
1차 차분이란 t시점의 데이터와 t-1시점의 데이터의 차이
2차 차분이란 t시점의 데이터와 t-2시점의 데이터의 차이
d차 차분이란 t시점의 데이터와 t-d시점의 데이터의 차이
X(원래 데이터)는 nonstationary여도 differencing을 한 결과(Y)는 stationary로 바뀔 확률이 매우 크다

차분 : 현 시점 데이터에서 d시점 이전 데이터를 뺀 것

ARIMA - Order of Differencing

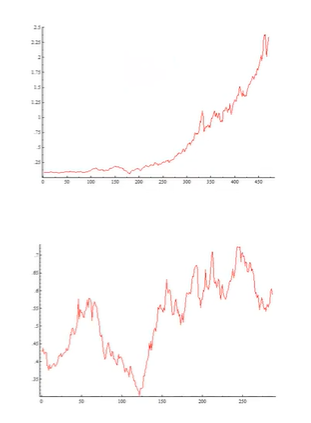
만약 original 데이터가 stationary이면 differencing은 필요없다.
만약 original 데이터가 constant average trend(일정하게 증가하거나 감소하는 패턴)이면 1차 차분이면 충분하다.
아래쪽의 그래프와 같이 더 복잡한 패턴을 가지고 있다면 2차 차분까지 가야된다.
대부분의 데이터가 2차 차분으로 충분하다.
3차 차분까지 했을 때 stationary가 되는 데이터는 AR,MA,ARMA 모델로는 적합하지 않은 데이터라고 생각하면 됨.

1st Differencing (1차 차분)

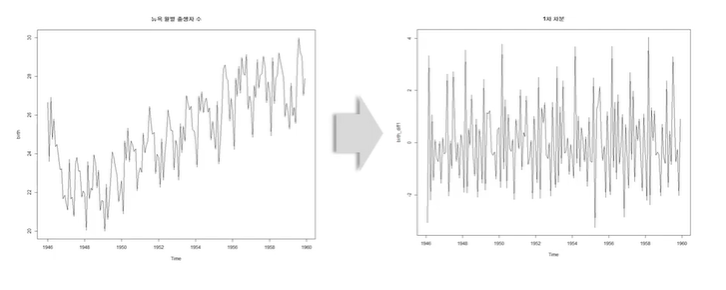
2nd Differencing (2차 차분)

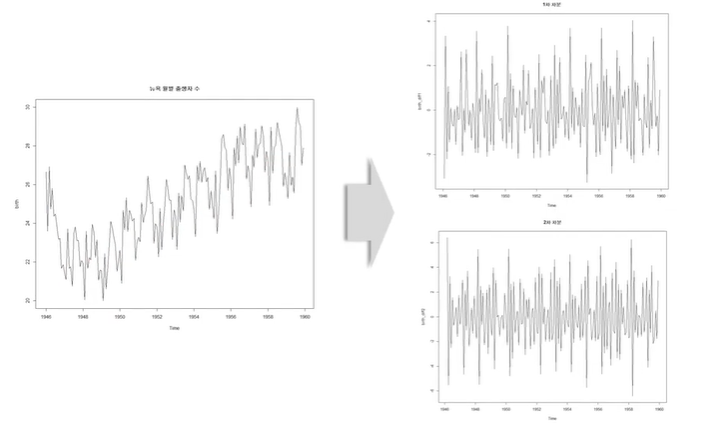
1차와 2차의 차이가 없으므로 2차 차분까지 할 필요가 없어보임.

=> nonstationary가 stationary로 변했는지 그냥 봤을 때는 잘 모르므로 ACF를 확인하자.

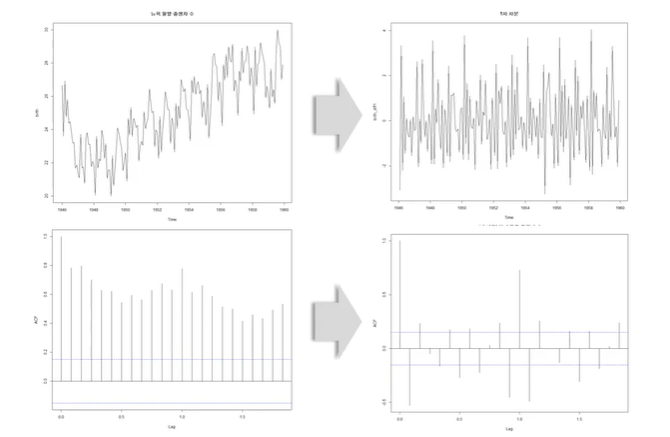
원래 데이터는 ACF에서 일정하게 감소하는 패턴
1차 차분한 것은 일정한 패턴이 없다.

실제 데이터로 해보기

Box-Jenkins ARIMA Procedure

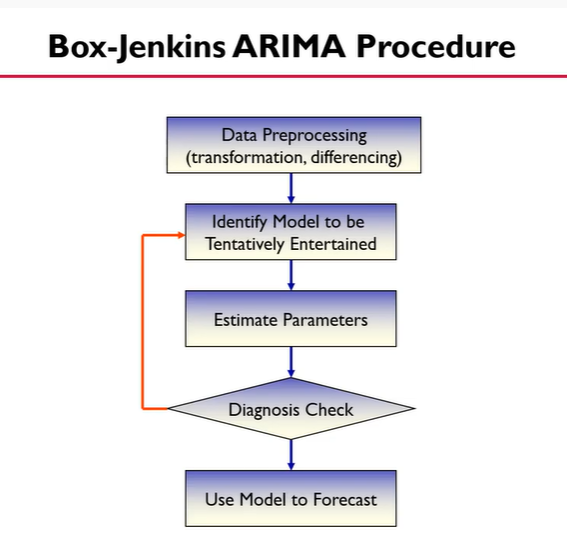
1. 데이터 전처리 (데이터가 nonstationary일 때, transformation이나 differencing을 이용해서 stationary하게 만듦)
2. 시범적으로 해볼 모델을 선정
3. 파라미터 추정
4. 모델이 괜찮은지 체크 => 괜찮지 않다면 2번 스텝으로
5. 예측하기

Raw Data Plotting

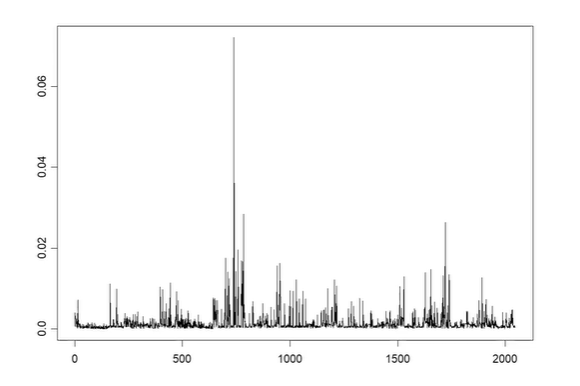
이 그래프만 보면 stationary한지 잘 모르겠으므로 ACF를 확인하자.

Autocorrelation Function - Check Stationarity

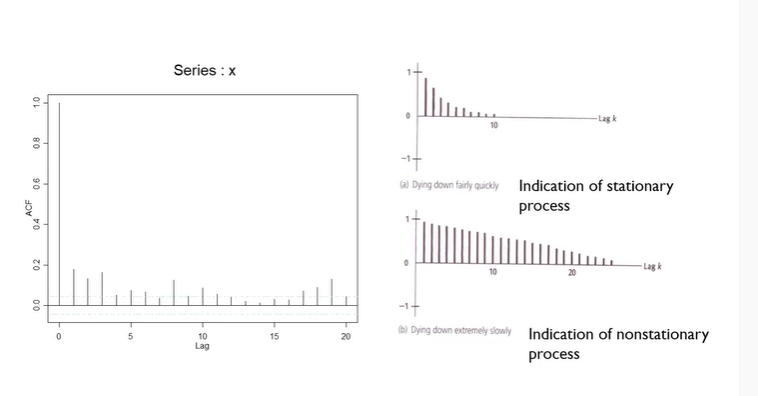
lag가 0일 때는 ACF는 1이다. lag가 0은 자기자신과의 correlation이기 때문이다. 따라서 lag 1일 때부터 보자. 왼쪽 그래프를 보면 천천히 줄어드는 패턴이므로 nonstationary인 것을 알 수 있다.
=> stationary하게 만들어줘야된다! => 차분!

Differencing

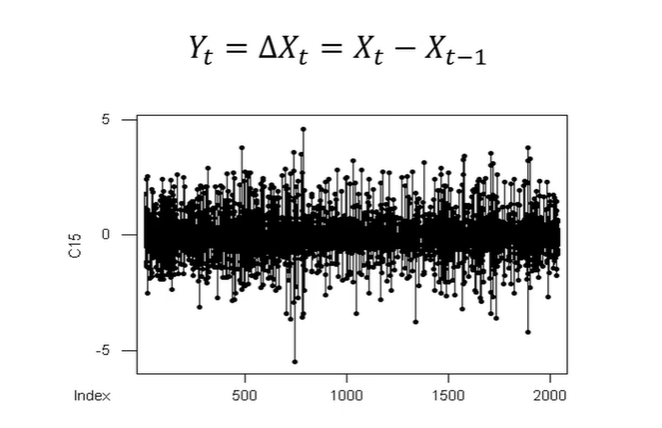
1차 차분을 해준 결과이다.
=> stationary가 됐을까? => ACF로 다시 확인

ACF after Differencing

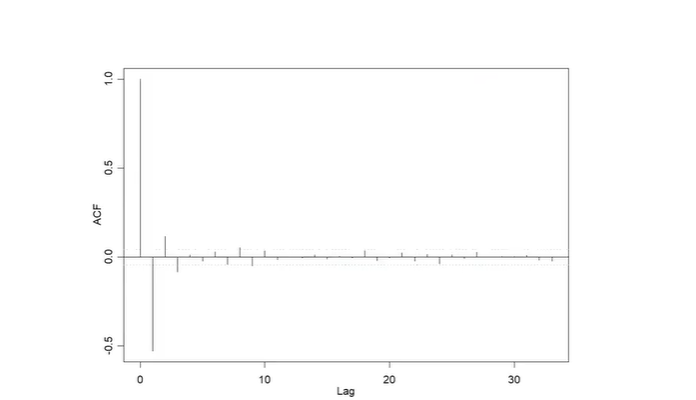
lag 1 이후에 확 떨어진다 => stationary가 잘 됐다!

Identification ARIMA Model

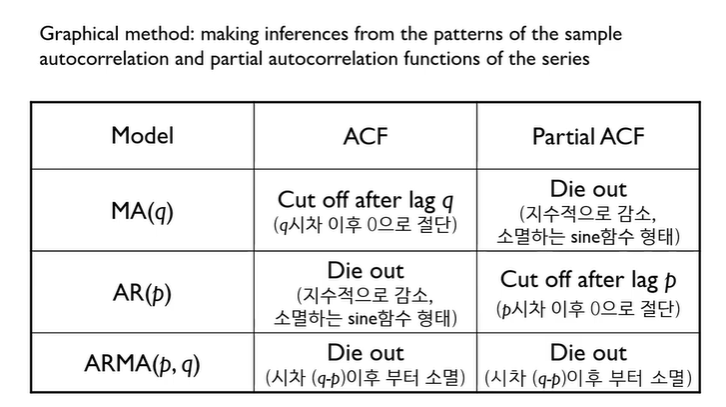
시범적인 모델을 먼저 찾아보자! => Graphical method 사용 (주관적임) => 시계열데이터의 autocorrelation과 partial autocorrelation function의 패턴을 통해 결정한다
MA, AR ,ARMA 모델 중 뭘로 할지 정해야 된다.
- MA모델을 선택하는 경우 : ACF는 lag q 이후에 절단되는 패턴을 보임/PACF는 천천히 감소 하는 패턴을 보일 때
- AR모델을 선택하는 경우 :PACF이 lag p 이후에 확 떨어지고 ACF가 지수적으로 감소 or sine함수 형태로 소멸할 때
- ARMA모델은 선택하는 경우 : ACF와 PACF가 (q-p)시점 이후부터 떨어질 떄

Behavior ACF

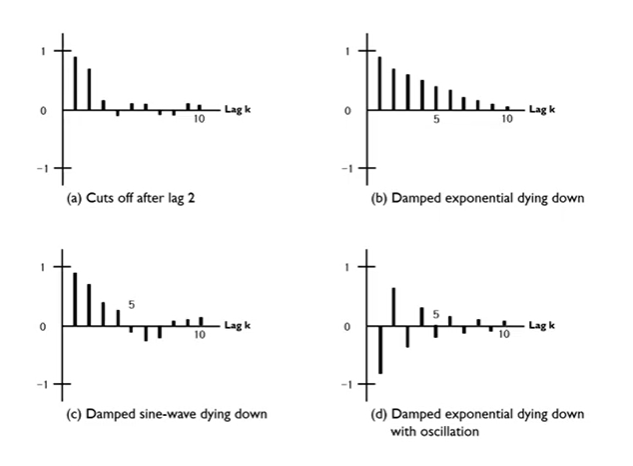
(a) : lag 2 이후에 확 감소한다. (Cut off)
(b) : 지수적으로 천천히 감소 (Die out/Die down)
(c) : sine함수 모양으로 감소 (Die out/Die down)
(d) : 0을 기준으로 + - 왔다갔다 하면서 점차적으로 줄어드는 경우 (Die out with osciliation)

Identification ARIMA Model

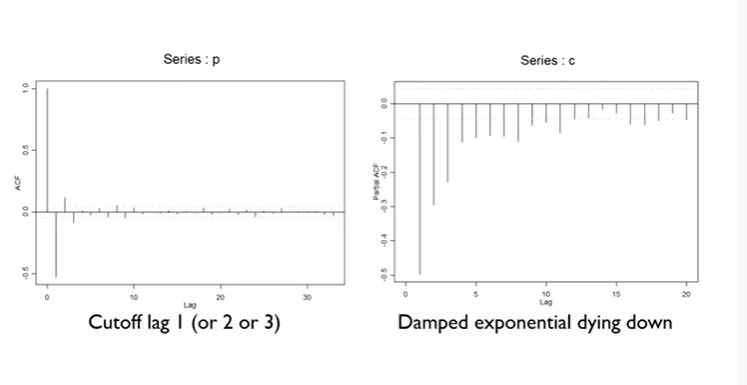
ACF : lag 1 이후에 쭉 떨어짐 (cut off)
PACF : 점점 감소함 (die down)
=> Graphical method에 의하면 MA 모델이 적합, lag 1 이후에 떨어졌으므로 MA(1)이 적합
=> 첫 시작은 일단 MA(1)으로!

Parameter Estimation

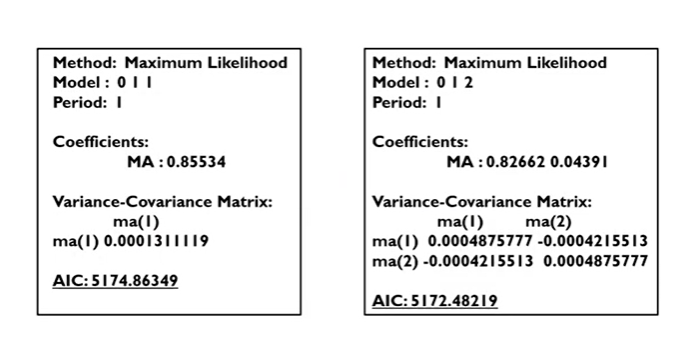
Model : 0 1 1 => 각각 AR(p), d, MA(q)를 의미함 => ARIMA(0,1,1) 모델을 의미

AIC는 작을수록 좋다.
오른쪽은 ARIMA(0,1,2)로 시도해본 것이다.

Determination of Model

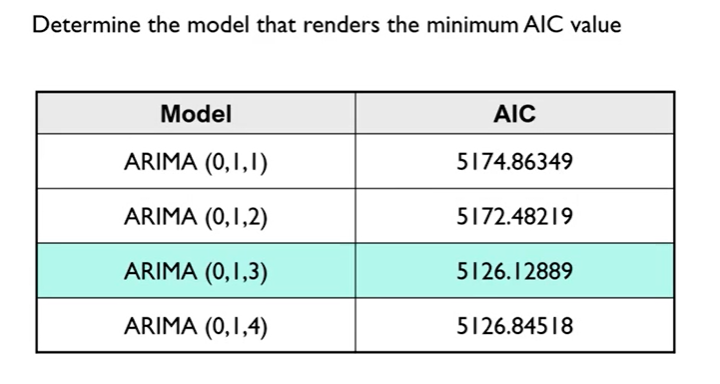
근방에 있는 모델들을 몇개 해본다. => ARIMA(0,1,1)이 처음엔 좋다고 생각했는데 다른 것도 해보니 ARIMA(0,1,3)이 좋다고 판단할 수 있다. 다만 이 모델이 최종 모델은 아님.

Diagnosis - Performance Evalution

시범적인 모델이 결정이 되고 파라미터가 추정이 되면, 이것이 적절한지 체크해야된다.
residuals(시범적인 모델에서 나온 y 예측값과 실제 y값의 차이 = $\hat{y}$ - y)을 갖고 ACF plot을 다시 생성한다.
대부분의 residuals 값이 어떤 영역안에 들어와있고 40중 두세개 정도 나가면 OK

=> ARIMA(0,1,3)의 residuals values를 구해서 ACF plot을 그리면?

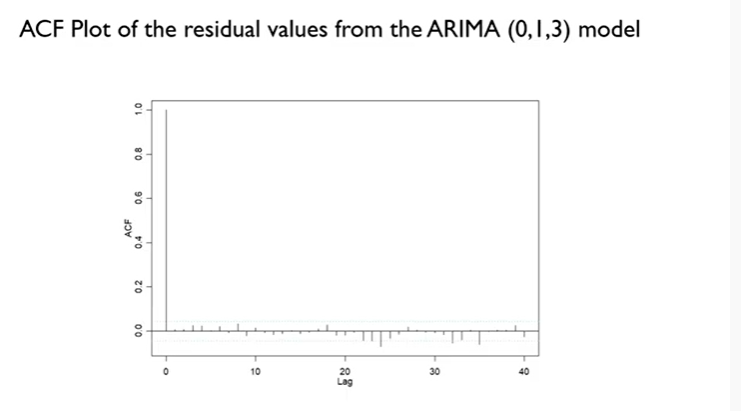
하늘색 선 : upper, lower bound
대부분이 bound 안에 들어온다. => 이 모델 OK! => 최종 모델로 결정!

Forecasting

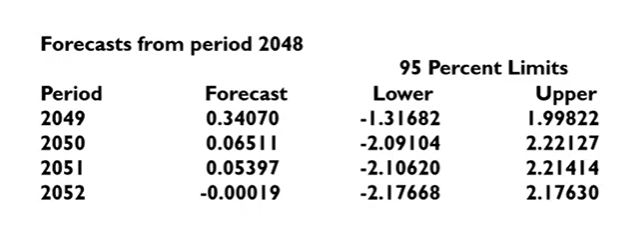
미래(2048년)의 값을 예측하기!

ARIMA(p,d,q)에서 p,d,q 구하는 법

=> Graphical method을 사용해서 주관적으로 판단했지만 이 방법대로 패턴이 보이지 않는 경우도 많다
=> 그래서 보통 p랑 q를 바꿔본다. for문으로 p를 1~20, q를 1~20 이런 식으로 여러 경우의 수를 돌려보고 AIC와 같은 평가지표를 보고 결정한다.