푸리에 변환은 신호처리와 관련된 변환이다. 주로, 소리(1d signal)를 변환하는 데 쓰인다.
소리를 파형으로 나타내면, 가로 축은 시간이 되고, 세로 축은 세기가 될 것이다. 이를 time domain에서 1d signal이라 한다.
이 때, 이 신호에 대해 푸리에 변환을 거치게 되면, 주파수 도메인에서의 크기로 설명할 수 있다. 즉, 높은 음(주파수 크다)과 낮은 음(주파수 낮다)을 구별할 수 있는 신호를 해석할 수 있게 된다.
이를 영상 및 이미지(2D signal)에 적용할 수도 있다.
영상에서 높은 주파수, 낮은 주파수라 함은, EDGE나 무늬같은 픽셀 값이 빠르게 변화하는 경우 높은 주파수를 가지고, 밋밋하게 변화하는 경우 낮은 주파수를 가진다고 볼 수 있다.
즉, 2d signal에서 푸리에 변환이라 함은 image, space domain을 주파수 도메인으로 바꿔주는 과정이다.
보통 이미지들은 저주파수 성질을 훨씬 많이 띤다.
DFT(2D Discrete Fourier Transform)은 원래 연산이 오래 걸리지만, 이를 좀 개선한 FFT(Fast Fourier Transform)를
[opencv 홈페이지](http://docs.opencv.org/master/d6/d00/tutorial_py_root.html 에는 Numpy와 OpenCV를 활용한 FFT 방법이 예시로 나와있다.
당장 푸리에 변환을 거치고나면 복소수 등이 포함되어 있기 때문에 다이렉트하게 시각화할 수는 없어, 절대값을 씌운 magnitude와 페이즈를 따로따로 시각화해 확인하곤 한다.
또한, 푸리에 변환을 한 뒤 나온 결과값은 좌측 상단이 zero 주파수로 되어 있다. 다만, 그 영점은 모서리에 있는 것보다 중앙에 있는 것이 훨씬 보기 편한데, 복소수 등 음수도 포함되기 때문이다. 그래서 translation 과정 또한 거치게 된다.
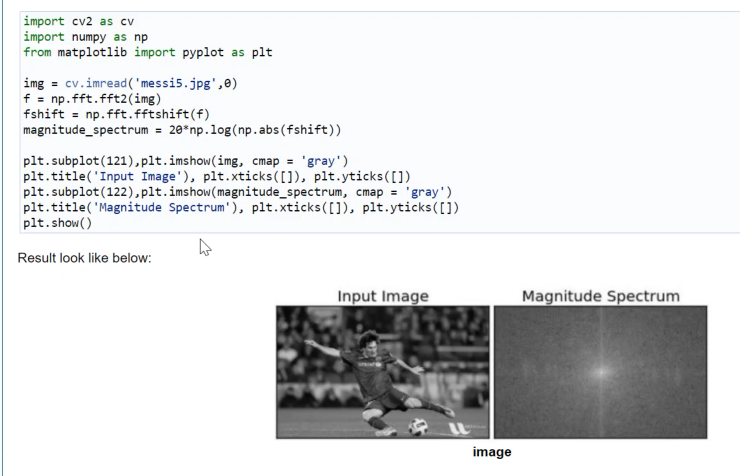
위에서 말했듯, 영상(이미지)는 zero 주파수(저주파수) 성분이 제일 많은 것을 볼 수 있다.
이런 푸리에 변환은 filtering을 하는 데 자주 쓰인다.
원래, 이미지에 블러를 씌우기 위해서는 kernel을 통해 convolution을 진행해야 한다. 이는 연산을 굉장히 많이 소모하게 되는데, 푸리에변환에서는 이미지 도메인에서 푸리에 변환을 통해 얻은 frequency 값을 얻고, kernel에도 푸리에변환을 적용해서 얻은 frequency 값을 얻고, 이를 단순히 곱해 inverse transformation을 진행하면 최종 결과 값을 얻을 수 있게 된다(속도 자체는 느려질 수도 있으나, 연산이 굉장히 간단하다).
in Numpy
아래 예시에서는, high pass filtering(즉, 고주파수만 통과시키는 필터)를 진행하였다.
즉, magnitude Spectrum의 중간 값을 기준으로 주변의 값을 0으로 만들어준다. 그 후, 역푸리에 변환을 위해 다시 영점을 중간에서 모서리로 translation 해준다. 그 후 inverse translation을 통해 최종적인 output을 얻게 된다.
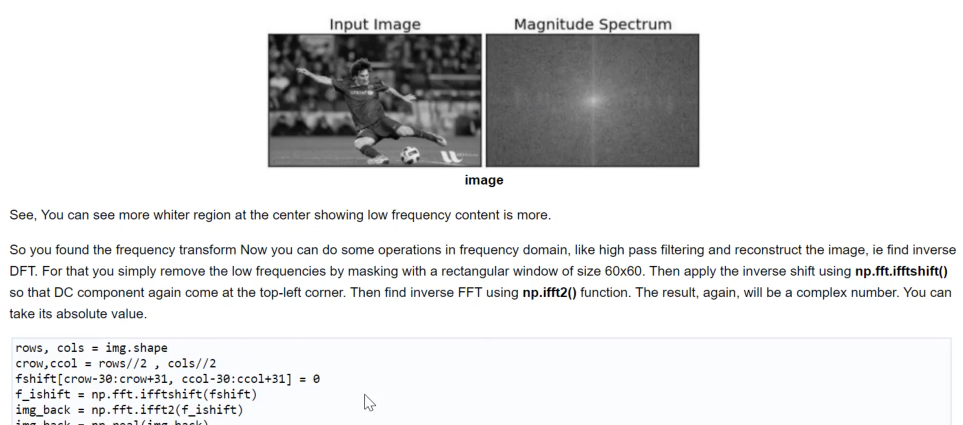
그 결과, 아래와 같이 고주파수를 나타내는 edge만 살아있는 것을 볼 수 있다.
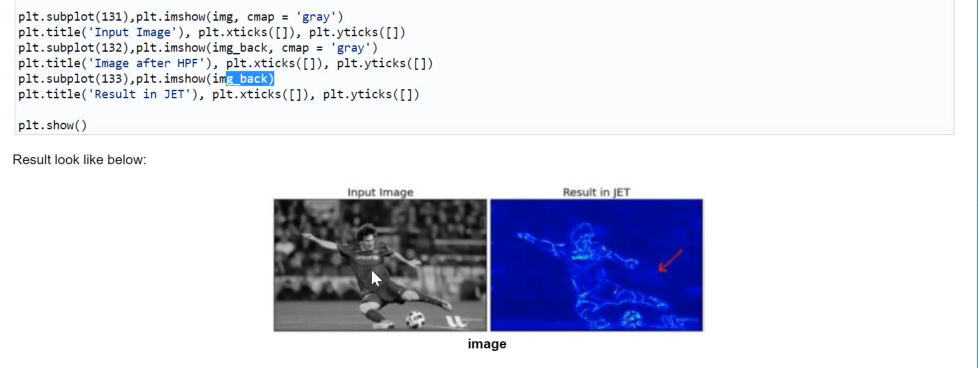
in OpenCV
opencv에도 cv.DFT, cv.FFT와 같은 푸리에 변환 함수를 사용할 수 있다.
low pass filtering을 진행해보자. 즉, Magnitude Spectrum의 중간 값(저주파수)를 1로 키워준 mask를 만든 후, 푸리에 변환을 거친 input 값과 mask를 곱해준다. 그 후 다시 이미지를 복원하면 된다.
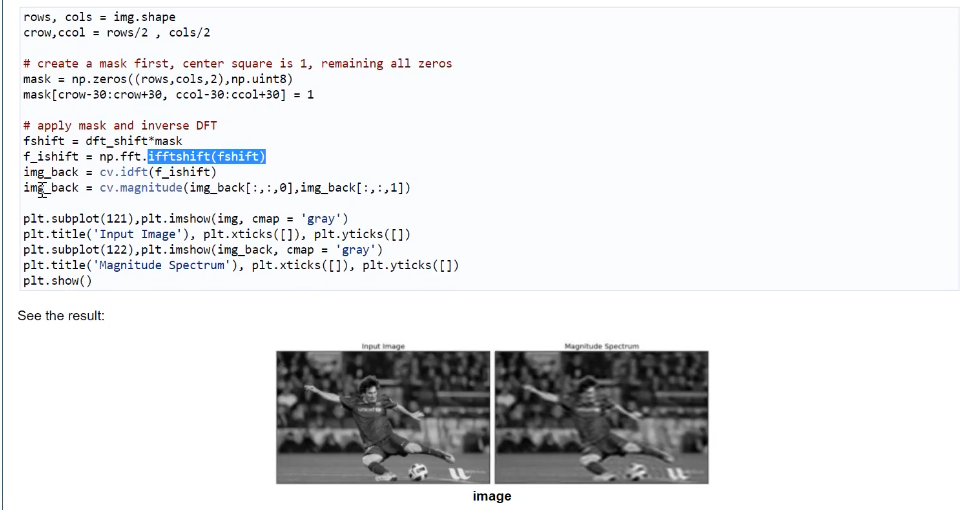
그러면 영상의 밋밋한 부분들만 나와있는 것을 볼 수 있다(like gaussian blurring)
요즘 CV에서는 잘 쓰이지 않지만, 주파수 단위에서의 신호분석이 필요한 경우 자주 쓰인다.