HiPPO

Abstract

• derivation of Legendre Memory Unit → GRU
• time scale robustness, fast update, bounded gradients
• empirically captuer temporal dependencies

Intro

• Memory : core aspect of modeling long-term and complex dependencies, storing and incorporating information from prev time steps
  • 한정된 저장공간에서 축적된 정보를 어떻게 잘 끌어모을 것인가
  • 기존 모델들은 prior info. 가 필요했으며 범위 밖에서는 효과가 없음. distribution shift에 대처할 수 없음
• To design better memory rep.
  • unified view of current methods
  • dependencies of any length w.o priors
  • theoretical understanding of mem. mechanism
• Memory = Online function approximation : storing optimal coefficients in terms of some basis functions
  • approximation w.r.t a measure that sepcifies the importance of each time in the past
  • 근사 함수가 주어지면 자연히 orthogonal polynomial이 등장하게 됨 (최적 파라미터를 closed form으로 구할 수 있게 됨)
    • approximation theory & signal processing 참고
• HiPPo : high-order polynomial projection operators : produces operators that project arbitrary functions onto the space of orthogonal polynomials w.r.t given measure
  • 미분방정식으로 정리하여 표현할 수 있음

HiPPO Framework

• Online function approx. = learning memory rep.

Problem setup

• Given input $f(t) \in \mathtt{R}$, we should know cumulative function $f_{\le t} := f(x)|_{x\le t}$
  • 그래야 이전 인풋 값을 이용해서 prediction을 할 수 있음
  • 전체 정보를 전부 저장할 수는 없기에 한정된 공간으로 잘 projection하는 것이 중요하다
  • 이를 위해 필요한 것 : 1. way to quantify approximation 2. suitable subspace
• Function Approximation with respect to a Measure
  • function space의 distance를 정의해야함
  • probability measure $\mu$
  • $\mu$ 에 대해 적분가능 함수 f, g의 내적은 아래와 같이 정의되며 이는 Hilbert space structure과 norm을 제시함
    $<f, g>_{\mu} = \int_0^{\inf}f(x)g(x)d\mu(x)$
    • hIlbert space = 유클리드 공간의 일반화, 복소공간이라고 볼 수 있음!
• Polynomial Basis expansion
  • 어떠한 N 차원 공간도 approximation의 대상이 될 수 있으며 N = order of approx. coeff
  • 다항공간에서 근사를 진행할 것임
• Online Approximation
  • t에 따라 변하는데,
  • Overall, we seek some g(t) ∈ G that minimizes ‖f≤t − g(t)‖L2(μ(t)).
  • 즉 input 공간에서 중요한 부분을 결정하는 mu를 다양한 근사, 최적화 방법으로 풀고자 하는 것임

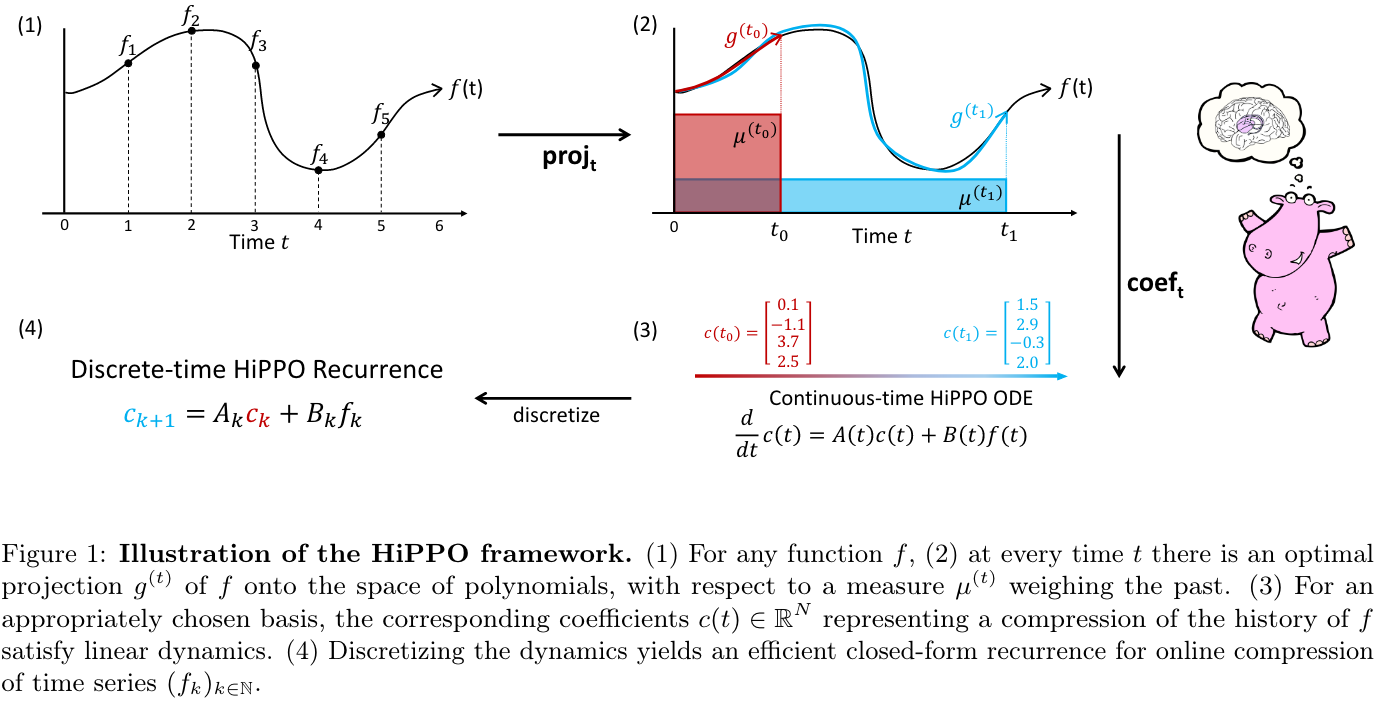
General HiPPO framework

• Calculating the projection through continuous dynamics
  • 근사 함수는 N 개 변수의 기저에 대한 expansion으로 표현할 수 있으므로 basis를 잘 고르는 것이 매우 중요하다
  • natural basis = set of orthogonal polynomials for the measure $\mu^{(i)}$ ⇒ coefficients of the optimal basis expansion $c_n^{(t)} = <f_{\le t}, g_n>_{\mu_{(t)}}$
  • differentiate the projection in t! self-similar relation allowing coefficietns to evolve as an ODE
• Online function Approximation
  • HiPPO는 projector과 coefficient extraction operator을 정의하느 매커니즘
  • 근사 오류를 최소화하는 방향으로 사영하며 대각 다항기저로 매핑함
  • 그래서 미분값을 미분방정식의 형태로 쓸 수 있음
  • discretized 면 실수값 범위에서도 연산이 됨

High Order Projection : measure families and HiPPO ODEs

• 다양한 mu(t)에 대해서 HiPPO를 적용해보자
  
• Translated Legendre : assign uniform weight to the most resent history $[t - \theta, t]$
  • $\theta$ : length of the sliding window(history being summarized)
• Translated Laguerre : exponentially decaying measure = more importance to recent history
  
• 이에 대해 HiPPO를 적용하면 Linear Time Invariant한 ODE로 정의가 가능함

HiPPO recurrences, from Continuous to Discrete Time with ODE discretization

• 어떻게 연속적인 Hippo를 discrete하게 바꿀 것인가?
• 연속 : 함수를 받아서 함수를 return
• 이산 : input sequence → implicit function $f(k * \Delta t) = f_k$→ ODE를 계산해서 $c(t)$를 얻음 → discretize back to $c_k = c(k * \Delta t)$
  • step size가 굉장히 중요함

Low order projection: Memory Mechanisms of Gated RNNs

• LagT 의 경우 A, B가 모두 1이 됨 → 단순히 Gated RNN으로 정리가 가능해짐
• 훨씬 넓은 범위로 정의가 가능해짐

HiPPO-LegS : Scaled Measures for Timescale Robustness

• 직관적으로 생각해봐도 sliding window 사이즈를 조절해가면서 예측하는 것이 옳다!
• scaled Legendre mesure : uniform weight to all history
  
• 앞서 정의했던 요소를 모두 만족시킴
• time scale robust : 결합법칙 만족
  • 따로 time scale hyperparam.이 존재하지 않는다!
• computational efficiency : multiplication by the squared matrix $A$